0 X 2 X 6
gasmanvison
Sep 17, 2025 · 5 min read
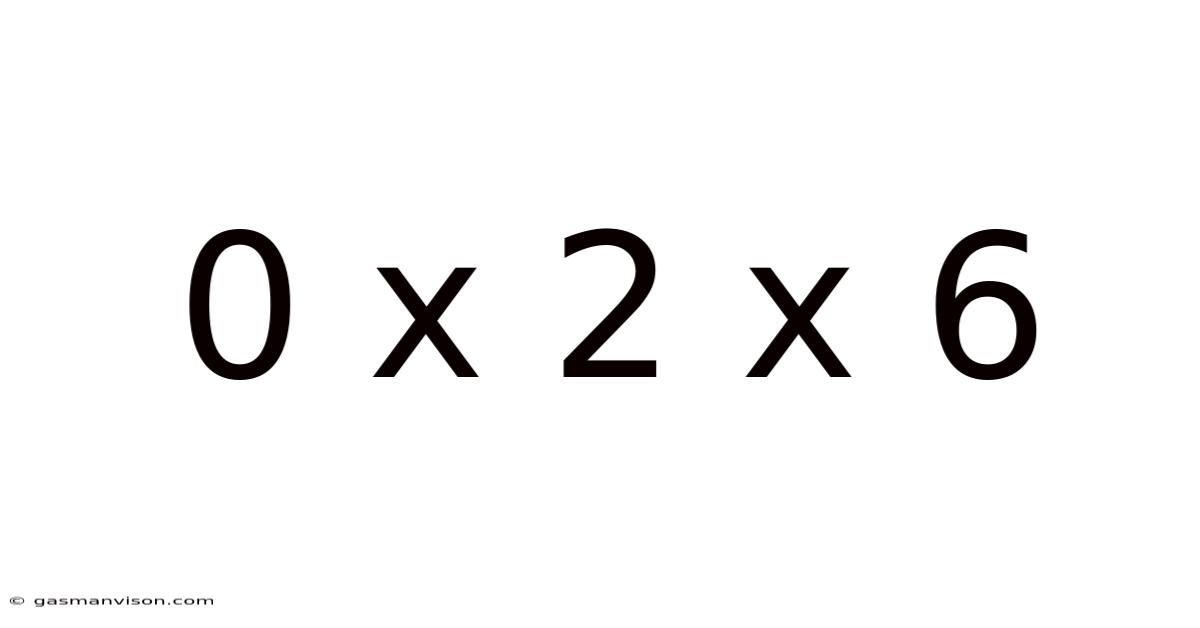
Table of Contents
Decoding 0 x 2 x 6: A Deep Dive into the Implications of Zero in Multiplication
The seemingly simple equation, 0 x 2 x 6, holds a surprising depth when examined through the lens of mathematics, programming, and even philosophical implications. While the answer – zero – is straightforward, understanding why the answer is zero reveals fundamental principles governing arithmetic operations and their broader applications. This article will explore the nuances of this equation, explaining its core mechanics, exploring its relevance in various fields, and delving into the often-overlooked significance of zero in mathematical operations.
Meta Description: Unravel the mystery behind 0 x 2 x 6. This in-depth exploration delves into the mathematical principles, programming applications, and philosophical implications of zero in multiplication, revealing its surprising significance.
Understanding the Fundamentals of Multiplication
Before dissecting 0 x 2 x 6, let's revisit the fundamental concept of multiplication. Multiplication is essentially repeated addition. For instance, 2 x 6 means adding 2 six times (2 + 2 + 2 + 2 + 2 + 2 = 12). This simple understanding forms the basis for more complex calculations. However, the introduction of zero introduces a unique element.
The Role of Zero in Multiplication: The Multiplicative Identity of Zero
The key to understanding 0 x 2 x 6 lies in the multiplicative identity of zero. This property states that any number multiplied by zero equals zero. This isn't just a rule; it's a direct consequence of the definition of multiplication. If multiplication is repeated addition, multiplying by zero means adding a number zero times – resulting in a sum of zero.
Let's break down 0 x 2 x 6 step-by-step:
-
0 x 2: Following the multiplicative identity of zero, 0 multiplied by any number is always 0. Therefore, 0 x 2 = 0.
-
(0 x 2) x 6: Now we have 0 x 6. Again, applying the multiplicative identity of zero, 0 x 6 = 0.
Therefore, the final answer to 0 x 2 x 6 is unequivocally 0.
Beyond the Basics: Exploring the Implications
The seemingly simple equation has far-reaching implications in various domains:
1. Arithmetic and Algebra:
The multiplicative identity of zero is a cornerstone of arithmetic and algebra. It simplifies complex equations and is crucial for solving problems involving variables and unknowns. Understanding this property is essential for mastering algebraic manipulations and solving equations involving multiplication and division. Without this fundamental principle, many mathematical operations would become significantly more complex and less efficient. It allows for the simplification of polynomials and the solution of simultaneous equations.
2. Computer Science and Programming:
In computer programming, the multiplicative identity of zero is fundamental to numerous algorithms and operations. Programming languages rely on this property to perform calculations efficiently and accurately. Consider scenarios involving arrays, matrix multiplication, or any operation involving large datasets where zero values are common. Understanding the behavior of zero in these contexts is critical for writing efficient and error-free code. Zero often acts as a placeholder or a flag, signaling the absence of a value, and its multiplicative property helps manage these instances effectively. For example, in calculating the sum of elements in an array where some elements might be zero, the multiplicative identity of zero ensures that these zero elements don't affect the total sum.
3. Set Theory and Combinatorics:
In set theory, the number of ways to choose zero elements from a set is always one (represented as 0! = 1). While this might seem counterintuitive, it's crucial for maintaining consistency in combinatorial calculations. This property plays a role in calculating probabilities and in solving problems related to combinations and permutations.
4. Calculus and Analysis:
The concept of zero plays a pivotal role in calculus, particularly in limits and derivatives. The concept of approaching zero, denoted by the limit notation, is essential in defining derivatives and understanding the behavior of functions near specific points.
5. Real-World Applications:
The multiplicative identity of zero has numerous practical applications in everyday life. Consider situations involving measurements, finances, or inventory management. Zero often represents the absence of something – zero dollars, zero units in stock, zero distance. The multiplicative property of zero ensures that these absences don't artificially inflate or deflate calculations. For instance, if a company has zero units of a certain product in stock, multiplying this quantity by the price per unit will correctly result in zero total revenue.
Addressing Potential Misconceptions
While the multiplicative identity of zero is straightforward, some common misconceptions might arise:
-
Division by Zero: While 0 x any number = 0, division by zero is undefined. This is because there's no number that, when multiplied by zero, results in a non-zero number. Division by zero leads to mathematical inconsistencies and is therefore not a valid operation.
-
Zero as a Placeholder: While zero serves as a placeholder in number systems (e.g., 10, 100), its fundamental role in multiplication remains consistent. Its positional value does not alter its multiplicative property.
-
Zero's Philosophical Implications: The concept of zero itself has profound philosophical implications. It represents nothingness, absence, and the void, concepts explored across various philosophical traditions. Its mathematical properties, while seemingly simple, reflect these deeper philosophical meanings.
Expanding the Exploration: Beyond 0 x 2 x 6
The equation 0 x 2 x 6 serves as a springboard for exploring broader mathematical concepts. It allows us to investigate the properties of real numbers, complex numbers, and even abstract algebraic structures. The seemingly simple equation unlocks a deeper understanding of mathematical principles and their applications across diverse fields.
Conclusion: The Unsung Power of Zero
The equation 0 x 2 x 6, though appearing trivial at first glance, reveals the fundamental importance of zero in mathematics and beyond. Its multiplicative identity simplifies calculations, underpins complex algorithms, and forms the basis for countless applications across various disciplines. A thorough understanding of this seemingly simple equation provides a strong foundation for advanced mathematical concepts and their practical uses. The seemingly simple "0" holds a surprising depth and power that shapes our understanding of the world around us. By understanding its properties, we unlock a deeper appreciation of the elegance and power of mathematics itself.
Latest Posts
Latest Posts
-
What Is 2 5 Equal To
Sep 17, 2025
-
Convert 185 Centimeters To Feet
Sep 17, 2025
-
Identifying And Safeguarding Pii Answers
Sep 17, 2025
-
What Is 45 Of 40
Sep 17, 2025
-
112 Ounces How Many Pounds
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 0 X 2 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.