1 024 Divided By 32
gasmanvison
Sep 17, 2025 · 5 min read
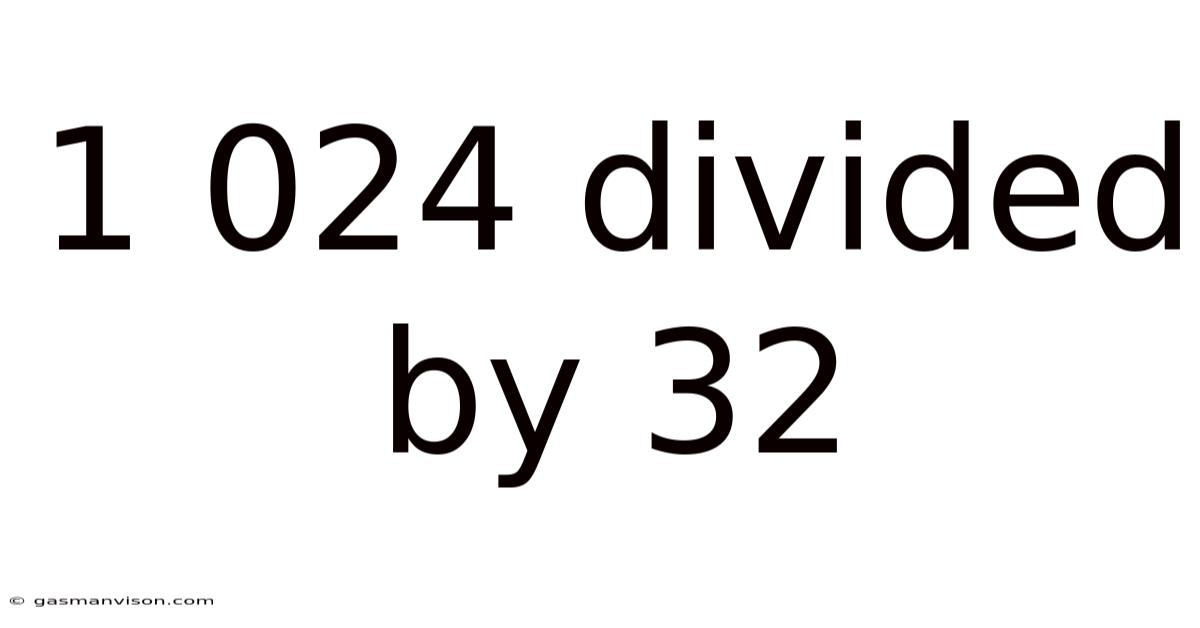
Table of Contents
1024 Divided by 32: A Deep Dive into Binary, Division, and Practical Applications
This article explores the seemingly simple calculation of 1024 divided by 32, delving beyond the basic arithmetic to uncover its significance in computer science, data storage, and other fields. We'll examine the mathematical process, explore its implications within the context of binary systems, and discuss real-world applications demonstrating its relevance. Understanding this seemingly simple division problem offers valuable insight into fundamental concepts crucial for anyone interested in technology.
What is 1024 divided by 32?
The answer, simply put, is 32. This basic arithmetic operation forms the foundation for a broader understanding of how data is organized and processed in digital systems.
Beyond the Basics: Understanding the Binary System
The number 1024 holds particular importance in computer science because it's a power of two (2<sup>10</sup>). This is directly related to the binary number system, the foundation of all digital computing. Binary uses only two digits, 0 and 1, to represent all numbers. Each digit represents a power of two. For example:
- 2<sup>0</sup> = 1
- 2<sup>1</sup> = 2
- 2<sup>2</sup> = 4
- 2<sup>3</sup> = 8
- 2<sup>4</sup> = 16
- 2<sup>5</sup> = 32
- 2<sup>6</sup> = 64
- 2<sup>7</sup> = 128
- 2<sup>8</sup> = 256
- 2<sup>9</sup> = 512
- 2<sup>10</sup> = 1024
Similarly, 32 is also a power of two (2<sup>5</sup>). Therefore, the division of 1024 by 32 can be represented as:
2<sup>10</sup> / 2<sup>5</sup> = 2<sup>(10-5)</sup> = 2<sup>5</sup> = 32
This highlights the elegant relationship between powers of two and how they simplify calculations within the binary framework.
Applications in Data Storage and Memory
The numbers 1024 and 32 frequently appear in discussions about computer memory and data storage. Let's explore some examples:
-
Kilobytes, Megabytes, Gigabytes, and Beyond: We often use prefixes like kilo, mega, and giga to denote units of data storage. However, in the context of computers, these prefixes don't follow the standard metric system (1000, 1000000, etc.). Instead, they are based on powers of two. A kilobyte (KB) is 1024 bytes, a megabyte (MB) is 1024 kilobytes (or 1024<sup>2</sup> bytes), a gigabyte (GB) is 1024 megabytes (or 1024<sup>3</sup> bytes), and so on. This binary system reflects how data is addressed and managed within the computer's memory.
-
Memory Addressing: Computers access data using memory addresses. These addresses are typically represented in binary, and the size of the addressable memory space is often a power of two. Understanding the relationship between 1024 and its divisors, like 32, helps in understanding how memory is organized and accessed.
-
Data Transfer Rates: Data transfer rates, such as those for network connections or storage devices, are often expressed in multiples of 32 or other powers of two. Understanding this relationship is crucial for analyzing network performance or storage device capabilities.
Practical Scenarios Illustrating the Significance
Let's consider a few scenarios that demonstrate the practical relevance of this seemingly simple division:
-
Dividing a large file: Imagine you have a 1024 MB file that you need to split into smaller, more manageable chunks. Dividing it into 32 MB segments creates 32 equally sized parts (1024 MB / 32 MB = 32 segments). This is a common task in data backup, data transmission, and parallel processing.
-
Memory allocation: A program might need to allocate 1024 bytes of memory. If each data structure requires 32 bytes, the program can allocate exactly 32 data structures (1024 bytes / 32 bytes = 32 structures). This is a fundamental concept in memory management.
-
Network data packets: Network data is often transmitted in packets. A network might transmit data in packets of 32 bytes. To transmit 1024 bytes, it would take 32 packets (1024 bytes / 32 bytes = 32 packets).
-
Image processing: Consider a grayscale image represented by 1024 pixels. If each pixel requires 32 bits of information (e.g., for color depth), the total amount of information required is 32,768 bits. This shows how the numbers 1024 and 32 relate to image resolution and color depth.
Beyond Simple Division: Exploring Related Concepts
The division of 1024 by 32 opens doors to exploring more advanced concepts:
-
Modular Arithmetic: The remainder after division plays a significant role in modular arithmetic, frequently used in cryptography and computer science algorithms. Understanding the relationship between the dividend, divisor, quotient, and remainder provides valuable insight into these advanced applications.
-
Number Systems: This example reinforces the importance of different number systems, highlighting the advantages of the binary system in digital computing.
-
Bit Manipulation: Many low-level programming tasks involve manipulating individual bits within a byte or word. Understanding how numbers like 1024 and 32 break down into binary representations is crucial for efficient bit manipulation.
Conclusion: The Unsung Importance of 1024/32
While the calculation of 1024 divided by 32 appears straightforward, its implications extend far beyond basic arithmetic. This seemingly simple division problem forms a cornerstone for understanding fundamental concepts in computer science, data storage, memory management, network communications, and various other technological fields. The relationship between powers of two and their divisors is crucial for the efficient and effective organization and processing of data in our digital world. By understanding this fundamental calculation, we gain a deeper appreciation for the intricate workings of the technology we use every day. This knowledge is invaluable for anyone seeking to understand the underlying principles of computing and its various applications. The seemingly simple act of dividing 1024 by 32 reveals a surprisingly complex and impactful relationship within the digital realm, reinforcing the importance of understanding the foundational elements of computer science. The prevalence of powers of two in computing highlights the inherent efficiency and elegance of binary systems, ultimately contributing to the seamless functioning of our digital world.
Latest Posts
Latest Posts
-
How Many Is 120 Inches
Sep 17, 2025
-
23 Repeating As A Fraction
Sep 17, 2025
-
What Is 40 Of 20 00
Sep 17, 2025
-
Which Structure Is Highlighted Ovary
Sep 17, 2025
-
Articles On Teens Going Pro
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 024 Divided By 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.