1 1/2 Times 1 1/2
gasmanvison
Sep 19, 2025 · 6 min read
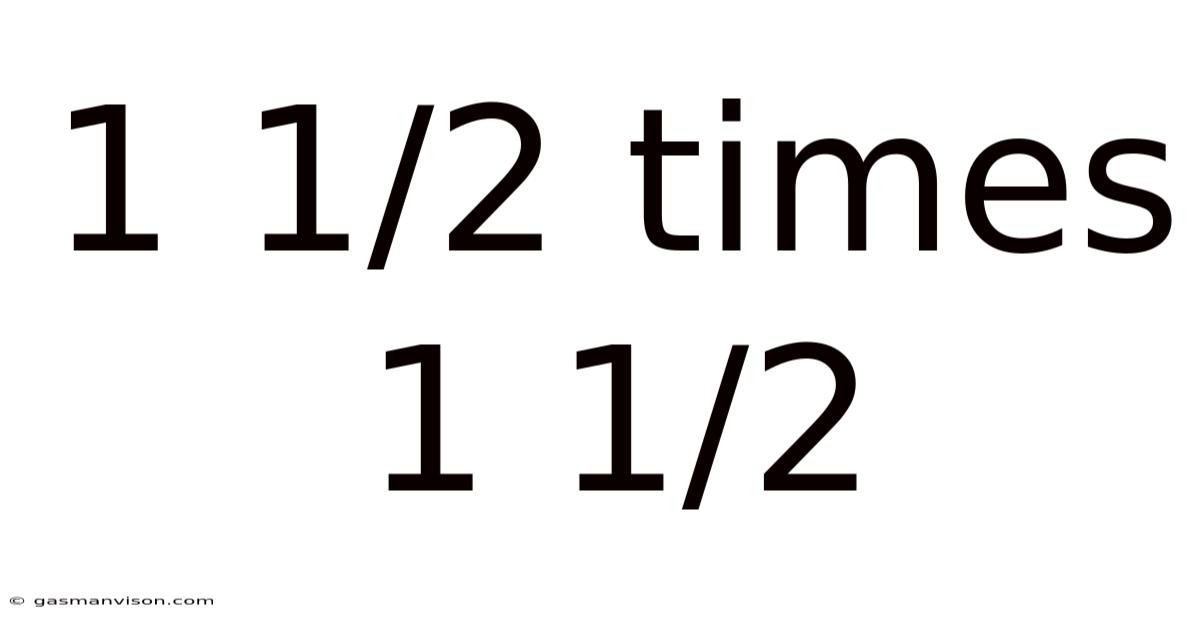
Table of Contents
Decoding 1 1/2 Times 1 1/2: A Deep Dive into Scaling and its Applications
This article explores the seemingly simple calculation of 1 1/2 times 1 1/2, expanding far beyond the basic arithmetic to reveal its significance in various fields, from everyday scaling to advanced mathematical concepts. We'll delve into different methods of calculation, explore real-world applications, and touch upon the broader implications of scaling and proportions in various contexts. Understanding this seemingly simple multiplication problem unlocks a deeper understanding of fundamental mathematical principles and their practical uses.
Understanding the Problem: 1 1/2 x 1 1/2
At its core, the problem "1 1/2 times 1 1/2" represents a scaling operation. We are increasing the size or quantity of something by a factor of one and a half. This can be visualized as expanding a square with sides of 1 1/2 units in length. The result is the area of that square. Let's examine the different approaches to solving this:
Methods of Calculation:
-
Converting to Improper Fractions: The most straightforward approach is to convert the mixed numbers (1 1/2) into improper fractions. 1 1/2 is equivalent to 3/2. Therefore, the problem becomes (3/2) x (3/2). Multiplying the numerators (3 x 3 = 9) and the denominators (2 x 2 = 4) gives us 9/4. Converting this back to a mixed number results in 2 1/4.
-
Decimal Conversion: Another common method is to convert the mixed numbers to decimals. 1 1/2 is equal to 1.5. Multiplying 1.5 by 1.5 gives us 2.25. This is equivalent to 2 1/4.
-
Distributive Property: We can also use the distributive property of multiplication. We can rewrite 1 1/2 as (1 + 1/2). Therefore, the calculation becomes (1 + 1/2) x (1 + 1/2). Expanding this using the FOIL method (First, Outer, Inner, Last) yields:
1 x 1 + 1 x (1/2) + (1/2) x 1 + (1/2) x (1/2) = 1 + 1/2 + 1/2 + 1/4 = 2 + 1/4 = 2 1/4
-
Visual Representation: Imagine a square with sides of 1 1/2 units. Divide this square into smaller squares and rectangles to visualize the multiplication. You will have one 1x1 square, two rectangles of 1/2 x 1, and one smaller square of 1/2 x 1/2. Adding the areas of these shapes will give you the total area of 2 1/4 square units.
Real-World Applications:
The seemingly simple calculation of 1 1/2 times 1 1/2 has numerous practical applications across various fields:
-
Scaling Recipes: If a recipe calls for a specific amount of ingredients and you want to increase the yield by 1 1/2 times, this calculation becomes essential. You would multiply the quantity of each ingredient by 1.5.
-
Enlarging Images or Drawings: Graphic designers and artists frequently need to scale images or drawings. Increasing the dimensions of an image by 1 1/2 times means multiplying both its width and height by 1.5. This will increase the area of the image by a factor of 2.25. Understanding the scaling factor is crucial for maintaining proportions and image quality.
-
Construction and Engineering: In construction and engineering, scaling is fundamental. If a blueprint needs to be enlarged or a model needs to be scaled up, the principles of scaling are crucial for ensuring accuracy and functionality. Calculating the new dimensions requires understanding the scaling factor and applying it consistently.
-
Fabric and Textile Design: Textile designers often work with repeating patterns. Understanding how a pattern scales when repeated helps them efficiently create larger designs. Scaling a smaller pattern by 1 1/2 could be useful in adjusting it to a larger surface.
-
Mapping and Cartography: Mapmakers use scaling to represent large geographical areas on smaller maps. The scale of a map is a ratio that relates the distance on the map to the actual distance on the ground. Understanding this scaling is crucial for accurate representation.
Beyond the Basics: Scaling and Proportions
The calculation of 1 1/2 x 1 1/2 provides a foundation for understanding broader concepts related to scaling and proportions:
-
Area Scaling: When you scale a two-dimensional object (like a square or rectangle) by a factor of 'x', its area is scaled by a factor of 'x²'. In our case, scaling by 1.5 results in an area increase of 1.5² = 2.25.
-
Volume Scaling: Similarly, when scaling a three-dimensional object by a factor of 'x', its volume scales by a factor of 'x³'. This is a crucial concept in fields like architecture and manufacturing, where volume calculations are essential.
-
Similar Figures: In geometry, similar figures have the same shape but different sizes. The ratio of corresponding sides of similar figures is constant, representing the scaling factor. Understanding this principle is important for solving problems involving similar triangles and other geometric shapes.
-
Proportional Reasoning: Proportional reasoning is a crucial skill in mathematics and problem-solving. Understanding proportions allows us to solve problems involving scaling, ratios, and rates. The calculation of 1 1/2 x 1 1/2 is a simple yet fundamental example of proportional reasoning.
Advanced Applications:
The principles of scaling extend far beyond the elementary level:
-
Computer Graphics: Computer graphics rely heavily on scaling and transformation matrices to manipulate images and 3D models. Understanding scaling factors is crucial for creating realistic and dynamic visuals.
-
Physics and Engineering: Scaling principles are applied in various areas of physics and engineering, including fluid dynamics, structural mechanics, and heat transfer. Understanding how forces and properties scale with size is crucial for designing and analyzing structures and systems.
-
Economics and Finance: In economics and finance, scaling is used to analyze growth rates, investment returns, and economic models. Understanding how economic variables scale with time and other factors is essential for making informed decisions.
Conclusion:
The seemingly simple problem of 1 1/2 times 1 1/2 serves as a gateway to understanding fundamental mathematical concepts like scaling, proportions, and the distributive property. Its applications span a wide range of fields, from everyday tasks like cooking to complex engineering and scientific calculations. By grasping the intricacies of this calculation, we not only improve our arithmetic skills but also develop a stronger foundation in mathematical reasoning and its practical relevance in the real world. The ability to understand and apply scaling principles is a valuable asset across numerous disciplines and contributes to a deeper understanding of the world around us. Furthermore, the ability to approach such problems from multiple angles, using different methods of calculation, strengthens problem-solving skills and fosters mathematical fluency. This fundamental calculation is a microcosm of the broader power and utility of mathematical principles.
Latest Posts
Latest Posts
-
Is Ncl3 Polar Or Nonpolar
Sep 19, 2025
-
How Tall Is 48 In
Sep 19, 2025
-
37 7 Degrees Celsius To Fahrenheit
Sep 19, 2025
-
Complete The One Variable Data Table
Sep 19, 2025
-
Making Waves Scholarship For Women
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 1/2 Times 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.