1 1/5 As A Decimal
gasmanvison
Sep 12, 2025 · 5 min read
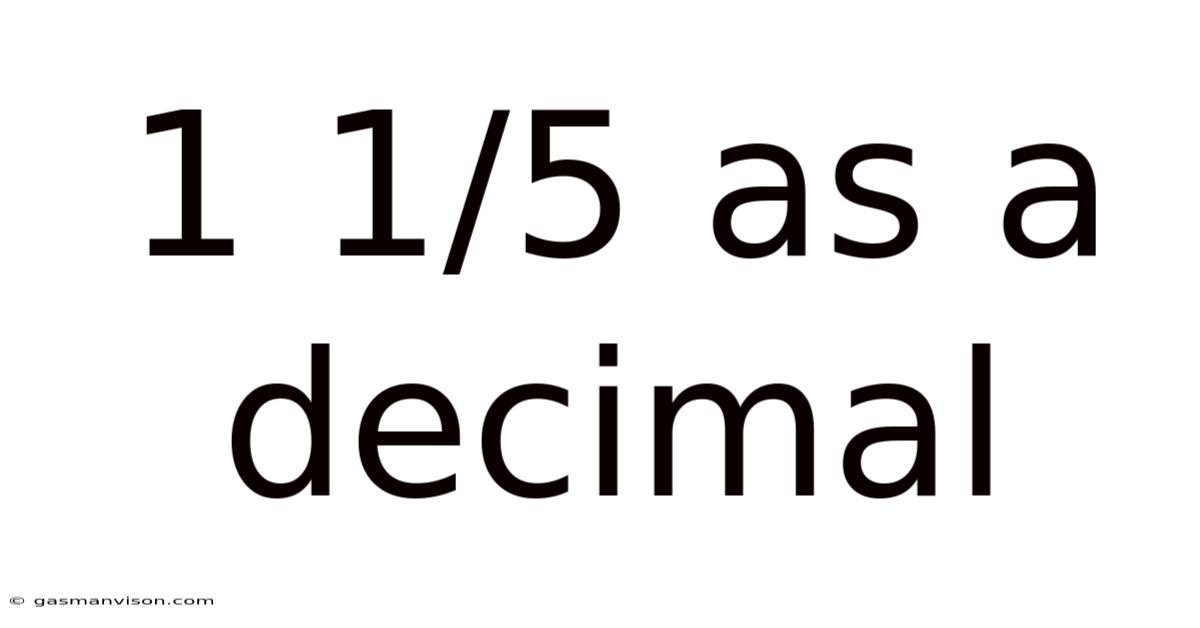
Table of Contents
1 1/5 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the mixed number 1 1/5 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying concepts. We'll also touch upon the importance of this conversion in various fields and offer practical examples to solidify your understanding.
Meta Description: Learn how to convert the mixed number 1 1/5 to its decimal equivalent. This detailed guide explores various methods, explains the underlying concepts, and provides practical examples for a comprehensive understanding.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's briefly revisit the concepts of mixed numbers and decimals. A mixed number combines a whole number and a fraction, such as 1 1/5. A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part. For example, 1.2 is a decimal where 1 is the whole number and 0.2 is the fractional part.
Converting fractions to decimals involves expressing the fractional part of a number as a decimal. This process is particularly useful in calculations involving both fractions and decimals, ensuring consistency and ease of computation.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is perhaps the most straightforward approach. We first convert the fraction 1/5 into its decimal equivalent and then add the whole number 1.
To convert 1/5 to a decimal, we perform the division: 1 ÷ 5 = 0.2.
Therefore, 1 1/5 as a decimal is 1 + 0.2 = 1.2.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
Another method involves converting the mixed number into an improper fraction first. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number).
To convert 1 1/5 to an improper fraction:
- Multiply the whole number (1) by the denominator (5): 1 * 5 = 5
- Add the numerator (1) to the result: 5 + 1 = 6
- Keep the same denominator (5): The improper fraction is 6/5.
Now, convert the improper fraction 6/5 to a decimal by performing the division: 6 ÷ 5 = 1.2.
Therefore, 1 1/5 as a decimal is 1.2.
Method 3: Understanding Place Value and Decimal Representation
This method offers a deeper understanding of the relationship between fractions and decimals. The denominator of the fraction 1/5 indicates the place value in the decimal system. Since the denominator is 5, we are dealing with the tenths place.
The numerator (1) represents the number of tenths. Therefore, 1/5 represents 1 tenth, which is written as 0.2. Adding the whole number 1 gives us 1.2.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is essential in numerous real-world applications:
-
Financial Calculations: Dealing with percentages, interest rates, and currency conversions often requires converting fractions to decimals for accurate calculations. For instance, calculating a 1/5 discount on a purchase requires converting 1/5 to 0.2 before multiplying it by the price.
-
Scientific and Engineering Applications: Many scientific and engineering calculations involve measurements and data representation. Converting fractions to decimals ensures consistency and simplifies calculations, particularly when using computers or calculators that primarily work with decimal numbers.
-
Measurement and Units: Converting between different units of measurement often involves fractions, which need to be converted to decimals for easier comparison and calculations. For example, converting inches to centimeters or pounds to kilograms might involve fractional values that need to be expressed as decimals.
-
Data Analysis and Statistics: Data analysis often involves calculating averages, percentages, and other statistical measures. Converting fractions to decimals ensures consistent data representation and simplifies statistical calculations.
-
Everyday Calculations: Even in everyday life, converting fractions to decimals can simplify tasks like sharing items equally, calculating recipe ingredients, or understanding discounts and sales.
Expanding on Decimal Conversions: More Complex Examples
While 1 1/5 provides a relatively simple example, the principles discussed apply to more complex fractions and mixed numbers. Let's explore a few more examples:
Example 1: Converting 2 3/4 to a decimal
- Convert the fraction 3/4 to a decimal: 3 ÷ 4 = 0.75
- Add the whole number: 2 + 0.75 = 2.75
Therefore, 2 3/4 as a decimal is 2.75.
Example 2: Converting 3 1/8 to a decimal
- Convert the fraction 1/8 to a decimal: 1 ÷ 8 = 0.125
- Add the whole number: 3 + 0.125 = 3.125
Therefore, 3 1/8 as a decimal is 3.125.
Example 3: Converting a recurring decimal
Some fractions, when converted to decimals, result in recurring decimals (decimals with a repeating pattern). For example, 1/3 = 0.3333... The three dots indicate that the 3 repeats infinitely. These are often expressed as 0.3̅ (the bar indicates the repeating digit). Understanding recurring decimals is important for accurate calculations and data representation.
Troubleshooting and Common Mistakes
When converting fractions to decimals, several common mistakes can occur:
-
Incorrect Division: Ensure you perform the division correctly. A simple calculation error can lead to an incorrect decimal value.
-
Misunderstanding of Place Value: Pay close attention to the place value of each digit in the decimal. Mistakes in place value can significantly affect the accuracy of the conversion.
-
Ignoring the Whole Number: Remember to add the whole number to the decimal representation of the fraction to obtain the complete decimal equivalent of the mixed number.
Conclusion
Converting fractions to decimals is a fundamental mathematical skill with broad applications. The examples and methods explained in this guide provide a solid foundation for understanding this process. Mastering this skill is crucial for success in various fields, from everyday calculations to complex scientific and engineering applications. Remember to practice regularly to solidify your understanding and to avoid common mistakes. By understanding the underlying principles of fractions and decimals, you can confidently tackle more complex conversions and apply this knowledge to various real-world scenarios. The ability to seamlessly transition between fractions and decimals showcases a comprehensive grasp of numerical representation and significantly enhances your mathematical proficiency.
Latest Posts
Latest Posts
-
Synonymous Most Nearly Means Asvab
Sep 12, 2025
-
Is Evaporation Endothermic Or Exothermic
Sep 12, 2025
-
Convert 210 Pounds To Kilograms
Sep 12, 2025
-
An Elderly Patient Might Understate
Sep 12, 2025
-
Longer Diagonal Of A Parallelogram
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.