1 3 Divided By 6
gasmanvison
Sep 10, 2025 · 5 min read
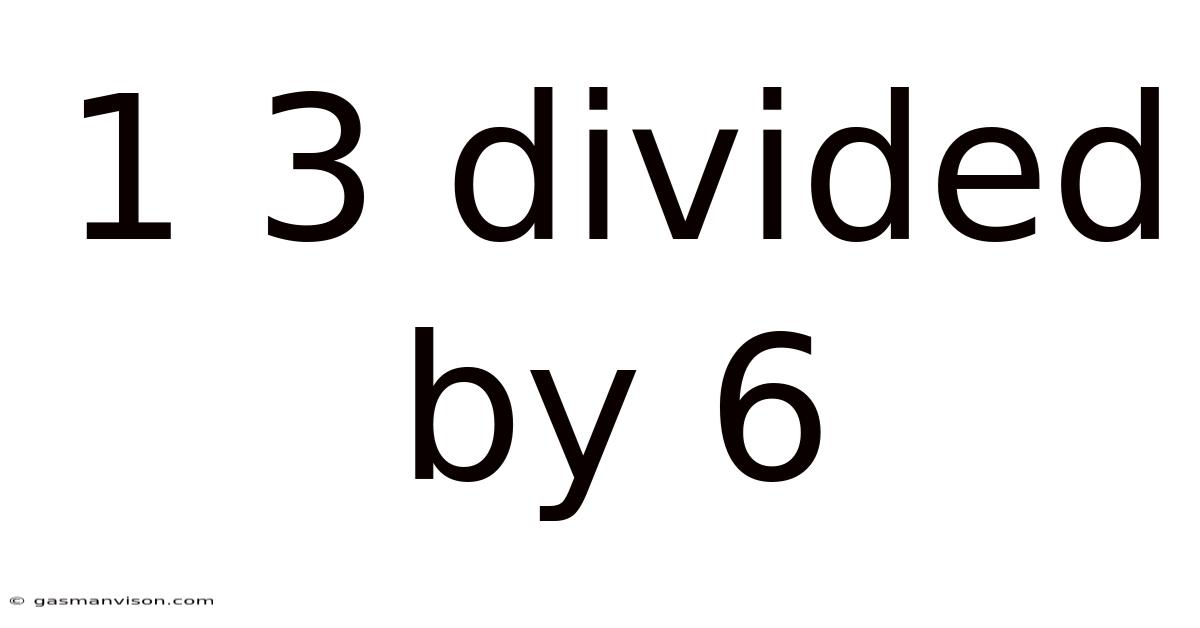
Table of Contents
Decoding 1 3/6: A Deep Dive into Fractions and Their Simplification
This article explores the seemingly simple mathematical expression "1 3/6," delving far beyond a simple calculation to examine the underlying principles of fractions, mixed numbers, simplification, and their practical applications. We'll uncover the steps involved in solving this problem, discuss the concepts of equivalent fractions, and explore how this fundamental operation applies to more complex mathematical scenarios. Understanding this seemingly basic concept is crucial for building a solid foundation in mathematics.
What is 1 3/6? Understanding Mixed Numbers and Improper Fractions
"1 3/6" is a mixed number, representing a combination of a whole number (1) and a proper fraction (3/6). A proper fraction has a numerator (the top number) smaller than the denominator (the bottom number). This mixed number represents a quantity greater than one but less than two. To manipulate and solve problems involving mixed numbers, it's often beneficial to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
To convert 1 3/6 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 6 = 6
- Add the numerator to the result: 6 + 3 = 9
- Keep the same denominator: The denominator remains 6.
Therefore, 1 3/6 is equivalent to the improper fraction 9/6.
Simplifying Fractions: The Concept of Equivalent Fractions
Both 3/6 and 9/6 can be simplified. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This process involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Let's simplify 3/6:
- Find the GCD of 3 and 6: The GCD of 3 and 6 is 3.
- Divide both the numerator and the denominator by the GCD: 3 ÷ 3 = 1 and 6 ÷ 3 = 2.
Therefore, 3/6 simplifies to 1/2. This means 3/6 and 1/2 are equivalent fractions; they represent the same value.
Now let's simplify 9/6:
- Find the GCD of 9 and 6: The GCD of 9 and 6 is 3.
- Divide both the numerator and the denominator by the GCD: 9 ÷ 3 = 3 and 6 ÷ 3 = 2.
Therefore, 9/6 simplifies to 3/2. This is an improper fraction, representing 1 1/2.
Putting it all together: Solving 1 3/6
We've established that 1 3/6 can be expressed as both 9/6 and 1 1/2. The simplified form, 1 1/2, provides the most concise and easily understandable representation of the value. Therefore, the solution to "1 3/6" is 1 1/2.
Real-World Applications of Fraction Simplification
The ability to simplify fractions isn't just a theoretical exercise; it has numerous practical applications across various fields:
-
Cooking and Baking: Recipes often require precise measurements, and simplifying fractions ensures accuracy in scaling recipes up or down. For instance, if a recipe calls for 3/6 of a cup of sugar, knowing it's equivalent to 1/2 a cup simplifies the measurement process.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Simplifying fractions ensures accurate calculations for dimensions, material quantities, and other critical aspects.
-
Finance and Accounting: Understanding fractions is crucial for managing budgets, calculating interest rates, and performing financial analyses. Simplifying fractions makes financial calculations more straightforward and less prone to errors.
-
Data Analysis and Statistics: Fractions and their simplification are vital for interpreting data, calculating percentages, and representing proportions in statistical analyses.
-
Everyday Life: From dividing a pizza among friends to calculating discounts, the ability to work with fractions is an invaluable skill applicable to numerous daily situations.
Beyond Simplification: Exploring Further Mathematical Concepts
The seemingly basic problem of "1 3/6" opens the door to a world of more complex mathematical concepts:
-
Decimal Representation: Fractions can be converted into decimals by dividing the numerator by the denominator. 1 1/2, for example, is equivalent to 1.5. Understanding the relationship between fractions and decimals is essential for various applications.
-
Percentage Calculation: Percentages represent fractions with a denominator of 100. 1 1/2 can be expressed as 150%. This conversion is frequently used in finance, statistics, and other fields.
-
Algebraic Manipulation: Fractions are fundamental elements in algebraic equations. Understanding fraction simplification and manipulation is crucial for solving algebraic problems.
-
Calculus and Advanced Mathematics: Fractions form the basis of many advanced mathematical concepts, including derivatives, integrals, and limits in calculus.
Conclusion: The Importance of Foundational Mathematical Skills
While the problem "1 3/6" appears simple, its solution involves a deeper understanding of fundamental mathematical principles like fractions, mixed numbers, equivalent fractions, and simplification. Mastering these concepts forms the cornerstone for success in more advanced mathematical studies and numerous practical applications in various fields. The ability to confidently simplify fractions contributes to accuracy, efficiency, and a more intuitive understanding of numerical relationships. This seemingly basic skill unlocks a world of mathematical possibilities, laying a solid foundation for future learning and problem-solving. Therefore, understanding and mastering the simplification of fractions, as demonstrated by solving "1 3/6," is far more significant than it initially appears. It’s a stepping stone to more complex mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
According To Virtue Ethics Emotions
Sep 10, 2025
-
Dna Replication In Chronological Order
Sep 10, 2025
-
What Is 10 Of 1200 00
Sep 10, 2025
-
What Is A Contour Interval
Sep 10, 2025
-
Is Salad Biotic Or Abiotic
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.