1 3 X 10 4
gasmanvison
Sep 05, 2025 · 6 min read
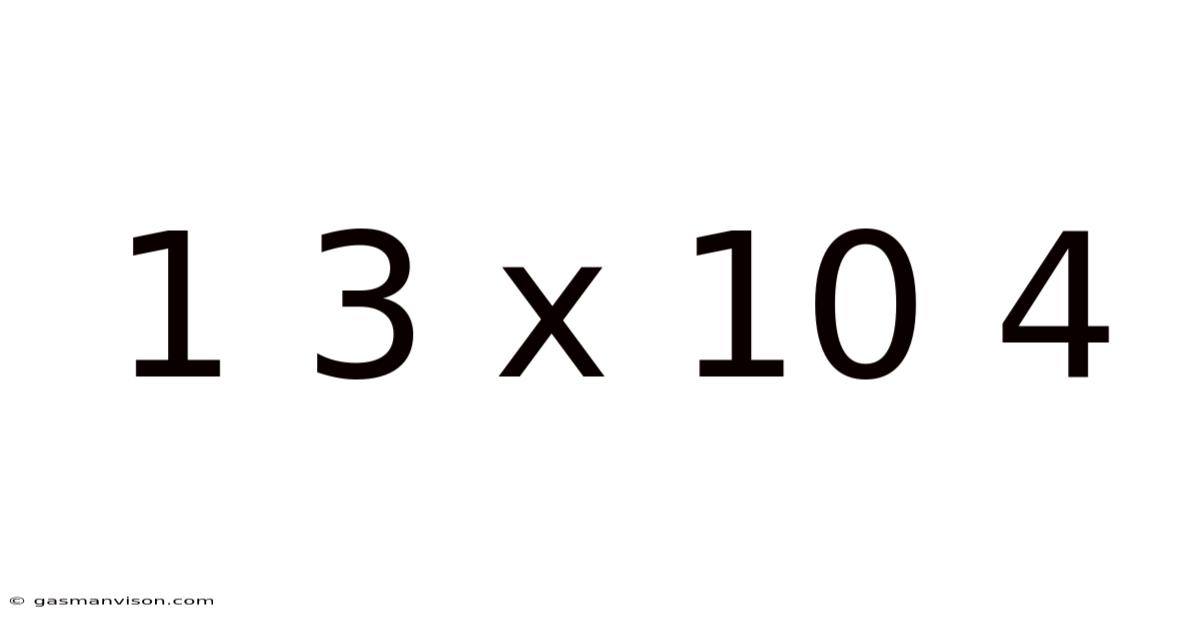
Table of Contents
Decoding 1.3 x 10⁴: Scientific Notation and its Applications
Scientific notation, a cornerstone of scientific and mathematical communication, provides a concise way to represent extremely large or extremely small numbers. This article delves into the meaning and applications of the specific number 1.3 x 10⁴, exploring its representation, conversions, and its significance across various fields. Understanding scientific notation is crucial for anyone working with data in science, engineering, finance, and numerous other disciplines. This article will unpack this concept, providing practical examples and demonstrating its versatility.
Understanding Scientific Notation
Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer exponent. This system simplifies the handling of very large or very small numbers, making them easier to read, write, and manipulate mathematically. The exponent 'b' indicates the number of places the decimal point needs to be moved to obtain the standard decimal form. A positive exponent signifies a large number, while a negative exponent indicates a small number.
For instance, the number 1,000,000 can be expressed in scientific notation as 1 x 10⁶. The decimal point is moved six places to the left to obtain the coefficient '1', resulting in a positive exponent of 6. Conversely, a very small number like 0.000001 can be written as 1 x 10⁻⁶. Here, the decimal point is moved six places to the right, leading to a negative exponent.
Dissecting 1.3 x 10⁴
Now let's focus on the specific number 1.3 x 10⁴. This notation indicates a number that is larger than 1 and less than 10, multiplied by 10 raised to the power of 4. The exponent 4 signifies that we need to move the decimal point four places to the right.
Performing this operation, we convert 1.3 x 10⁴ into its standard decimal form: 13,000. This demonstrates the convenience of scientific notation—it's much easier to write and comprehend 1.3 x 10⁴ than 13,000, especially when dealing with significantly larger numbers.
Real-World Applications of Numbers Similar to 1.3 x 10⁴
Numbers in this magnitude range appear frequently in various scientific and practical contexts. Consider these examples:
-
Population: The population of a moderately sized city might be in the tens of thousands. 13,000 could represent the population of a specific town or a particular demographic group within a larger city. Population density calculations, growth projections, and resource allocation strategies frequently utilize numbers of this scale.
-
Finance: In financial modeling, 13,000 could represent a company's daily revenue, the value of a specific investment portfolio, or the number of shares traded in a particular stock. Analyzing financial data often involves dealing with very large numbers, which are greatly simplified using scientific notation. This simplifies calculations related to compound interest, investment growth, or debt accumulation.
-
Environmental Science: In environmental studies, 13,000 could represent the number of trees in a specific forest area, the volume of water in a reservoir in cubic meters, or the number of migrating birds observed in a particular region. Analyzing environmental data often involves manipulating vast datasets, where scientific notation helps maintain clarity and accuracy.
-
Engineering: In engineering, this number could represent the weight of a component in kilograms, the number of units produced in a manufacturing process, or the tensile strength of a material. Precise calculations and data management are paramount in engineering, and scientific notation enhances accuracy.
-
Astronomy: While 13,000 is relatively small on a cosmic scale, understanding its representation is foundational to grasping larger astronomical numbers. For example, while not directly 13,000, the number of stars in a relatively small galaxy cluster could easily be represented using scientific notation with a much larger exponent.
-
Physics: In physics, this number could represent the number of particles in a sample, the energy level of a system, or the frequency of a wave. The applications of scientific notation are vast and vital for accurate calculations and data interpretation.
Calculations with 1.3 x 10⁴
Let's examine some basic mathematical operations involving 1.3 x 10⁴:
-
Addition and Subtraction: When adding or subtracting numbers in scientific notation, it's crucial to ensure that the exponents are the same. If they're not, convert one or both numbers to have the same exponent before performing the operation. For example, adding 1.3 x 10⁴ and 2.5 x 10⁴ is straightforward: (1.3 + 2.5) x 10⁴ = 3.8 x 10⁴ = 38,000.
-
Multiplication and Division: Multiplication and division in scientific notation are relatively simpler. When multiplying, multiply the coefficients and add the exponents. When dividing, divide the coefficients and subtract the exponents. For example, multiplying 1.3 x 10⁴ by 2 x 10² would be: (1.3 x 2) x 10<sup>(4+2)</sup> = 2.6 x 10⁶ = 2,600,000. Dividing 1.3 x 10⁴ by 2 x 10² would be: (1.3/2) x 10<sup>(4-2)</sup> = 0.65 x 10² = 65.
Significance and Importance
The significance of understanding and utilizing scientific notation extends beyond simply representing numbers. It is crucial for:
-
Data Management: Handling vast datasets, common in scientific research and data analysis, becomes significantly easier with the concise representation provided by scientific notation.
-
Computational Efficiency: Scientific notation simplifies calculations, particularly when dealing with extremely large or small numbers, leading to greater computational efficiency.
-
Clarity and Communication: Scientific notation enhances clarity and precision in scientific reports, publications, and presentations. It avoids ambiguity and makes data readily interpretable.
-
Error Reduction: The standardized format of scientific notation minimizes the risk of errors associated with writing and interpreting very large or small numbers in standard decimal form.
-
Cross-Disciplinary Application: The universal applicability of scientific notation facilitates seamless communication and collaboration across various scientific and engineering disciplines.
Beyond 1.3 x 10⁴: Expanding the Scope
While this article has focused on the specific number 1.3 x 10⁴, the principles discussed apply to all numbers expressed in scientific notation. Understanding these principles enables one to effectively manipulate and interpret numbers across a vast range of magnitudes, from the subatomic to the cosmic. Mastering scientific notation is a fundamental skill for anyone seeking to delve deeper into quantitative fields. It is a tool that empowers accurate calculations, simplifies complex data sets, and enhances the overall clarity and precision of scientific communication. It forms the bedrock of quantitative reasoning and analysis across countless disciplines. By understanding the underlying principles, one can effectively handle and interpret data representing diverse phenomena, from the microscopic world of atoms to the vast expanses of the universe. The ability to confidently work with scientific notation is essential for anyone pursuing a career in STEM fields or any area involving quantitative analysis.
Latest Posts
Latest Posts
-
Is 42 A Prime Number
Sep 05, 2025
-
What Is The Portable Pelican
Sep 05, 2025
-
Polymers That Contain Sugars
Sep 05, 2025
-
Electron Dot Structure For Lithium
Sep 05, 2025
-
Without Adjusting The Column Widths
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 10 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.