1/4 Is Greater Than 3/8
gasmanvison
Sep 14, 2025 · 5 min read
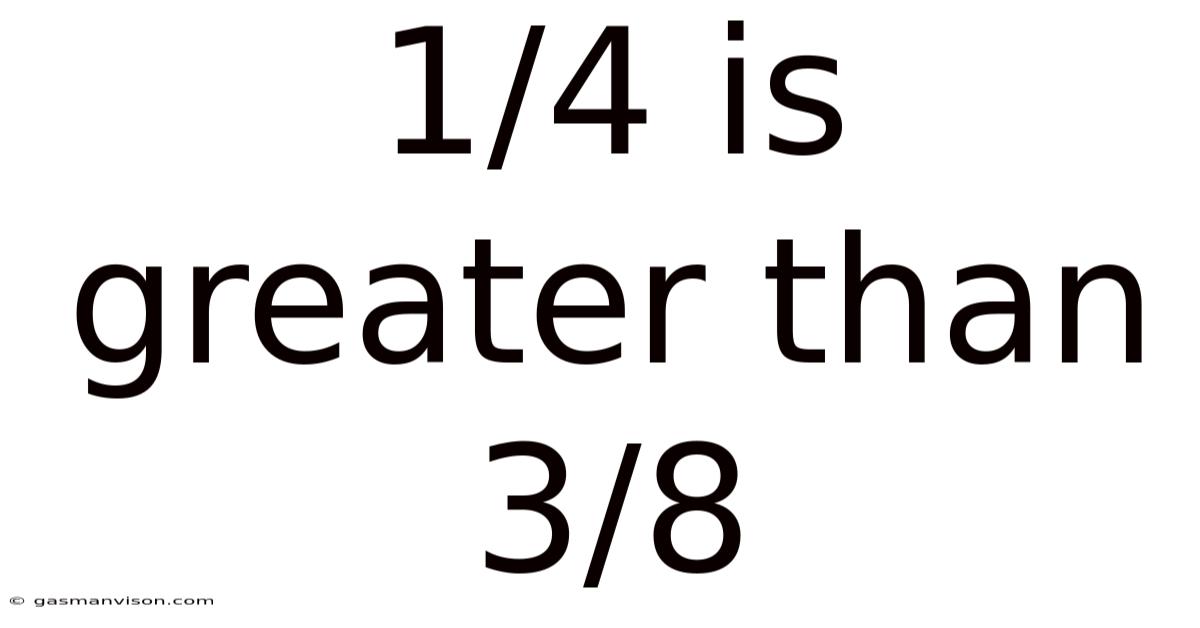
Table of Contents
Is 1/4 Greater Than 3/8? A Deep Dive into Fraction Comparison
Is 1/4 greater than 3/8? At first glance, this might seem like a simple question, easily answered with a quick calculation. However, understanding the nuances behind comparing fractions offers a valuable opportunity to reinforce fundamental math concepts and explore various problem-solving approaches. This article will not only definitively answer the question but also delve into the underlying principles of fraction comparison, providing you with the tools to tackle similar problems with confidence. We'll explore multiple methods, ensuring you grasp the concepts thoroughly, regardless of your mathematical background.
This article will cover:
- Understanding Fractions: A refresher on numerators, denominators, and their significance.
- Method 1: Finding a Common Denominator: The classic approach to comparing fractions.
- Method 2: Converting to Decimals: An alternative method using decimal equivalents.
- Method 3: Visual Representation: A helpful visual aid for understanding fraction relationships.
- Method 4: Cross-Multiplication: A quick method for comparing fractions.
- Real-World Applications: Examples of how fraction comparison is used in everyday life.
- Advanced Concepts: Extending the knowledge to more complex fraction comparisons.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the basic components of a fraction. A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator is 1 and the denominator is 4. This means we have 1 out of 4 equal parts. Similarly, in 3/8, we have 3 out of 8 equal parts.
Method 1: Finding a Common Denominator
This is the most fundamental method for comparing fractions. The core idea is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 1/4 and 3/8, we look for the least common multiple (LCM) of 4 and 8. The LCM of 4 and 8 is 8.
We can rewrite 1/4 with a denominator of 8 by multiplying both the numerator and the denominator by 2:
1/4 * 2/2 = 2/8
Now we can compare 2/8 and 3/8. Since 2 < 3, we conclude that 2/8 < 3/8, and therefore, 1/4 < 3/8. The initial assumption that 1/4 is greater than 3/8 is incorrect.
Method 2: Converting to Decimals
Another approach is to convert both fractions into decimals. This involves dividing the numerator by the denominator.
1/4 = 1 ÷ 4 = 0.25
3/8 = 3 ÷ 8 = 0.375
Comparing the decimal equivalents, we see that 0.25 < 0.375. This confirms that 1/4 < 3/8.
Method 3: Visual Representation
Visual aids can be particularly helpful in understanding fraction comparisons, especially for beginners. Imagine a pizza cut into 4 slices (representing 1/4) and another pizza cut into 8 slices (representing 3/8).
If you take one slice from the first pizza (1/4), and three slices from the second pizza (3/8), you'll visually see that the three slices from the second pizza represent a larger portion than the single slice from the first pizza. This reinforces the concept that 1/4 < 3/8.
Method 4: Cross-Multiplication
This is a faster method for comparing two fractions. To compare fractions a/b and c/d, we cross-multiply:
- Multiply the numerator of the first fraction by the denominator of the second fraction (a * d).
- Multiply the numerator of the second fraction by the denominator of the first fraction (c * b).
Compare the results:
- If a * d > c * b, then a/b > c/d.
- If a * d < c * b, then a/b < c/d.
- If a * d = c * b, then a/b = c/d.
Let's apply this to 1/4 and 3/8:
1 * 8 = 8
3 * 4 = 12
Since 8 < 12, we conclude that 1/4 < 3/8.
Real-World Applications of Fraction Comparison
Understanding fraction comparison is crucial in various real-life scenarios:
- Cooking and Baking: Following recipes often requires comparing fractions to ensure the correct proportions of ingredients.
- Construction and Engineering: Precise measurements in construction and engineering projects rely on accurate fraction comparisons.
- Finance: Calculating interest rates and understanding portions of investments often involve working with fractions.
- Data Analysis: Representing and comparing data often involves fractions and percentages.
Advanced Concepts: Extending the Knowledge
The principles discussed here can be applied to more complex fraction comparisons involving:
- Mixed numbers: Numbers with a whole number part and a fraction part (e.g., 1 1/2). To compare mixed numbers, convert them into improper fractions (where the numerator is greater than the denominator) and then use the methods discussed earlier.
- Improper fractions: Fractions where the numerator is larger than the denominator (e.g., 5/4). These can be converted to mixed numbers for easier comparison.
- Comparing more than two fractions: To compare multiple fractions, find a common denominator for all the fractions and then compare the numerators.
Understanding fraction comparison is a fundamental skill in mathematics. Mastering the various techniques discussed above – finding a common denominator, converting to decimals, visual representation, and cross-multiplication – will empower you to confidently tackle a wide range of fraction-related problems. Remember that practice is key; the more you work with fractions, the more intuitive the comparisons will become. Don't hesitate to utilize visual aids and real-world examples to solidify your understanding. By developing a strong foundation in fraction comparison, you'll build a crucial skill applicable across many areas of life and further mathematical studies.
Latest Posts
Latest Posts
-
Unproctored Placement Assessment Answer Key
Sep 14, 2025
-
Scientific Name For A Sheep
Sep 14, 2025
-
Which Term Describes An Enzyme
Sep 14, 2025
-
Formula For Mercury Ii Oxide
Sep 14, 2025
-
48 Degrees Farenheit To Celcius
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Is Greater Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.