12 1000 As A Decimal
gasmanvison
Sep 13, 2025 · 5 min read
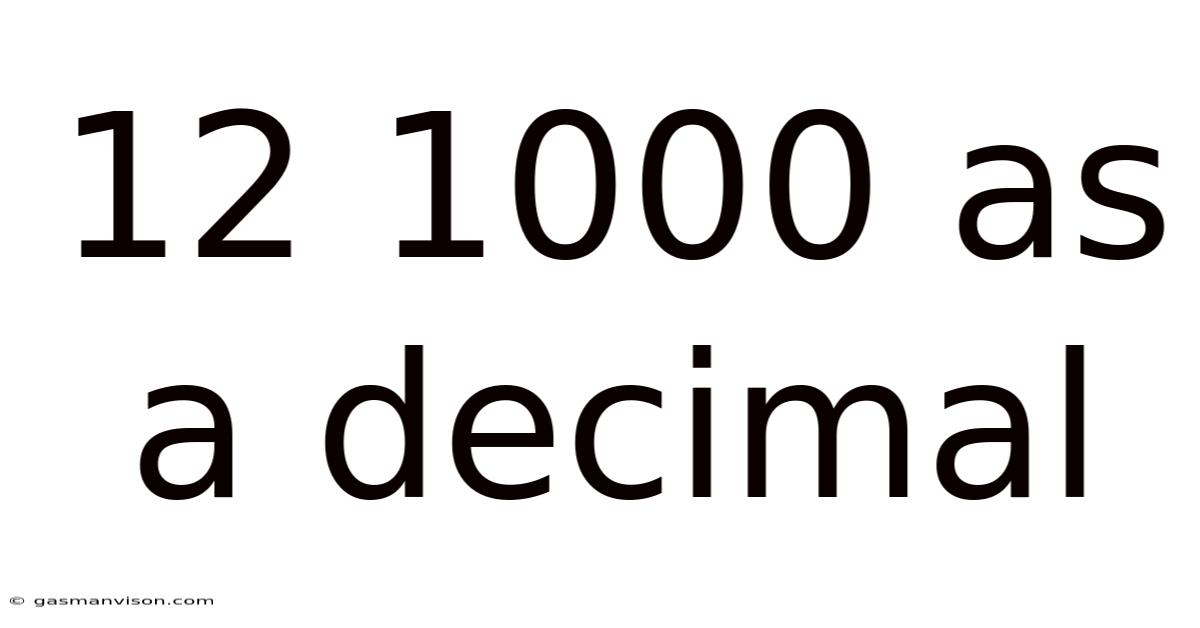
Table of Contents
12/1000 as a Decimal: A Comprehensive Guide to Understanding Fractions and Decimals
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to complex scientific computations. This article delves deep into the conversion of the fraction 12/1000 to its decimal equivalent, explaining the process in detail and exploring related concepts to solidify your understanding. We'll also look at different methods for handling similar fraction-to-decimal conversions, empowering you to tackle more challenging problems with confidence.
Understanding Fractions and Decimals:
Before diving into the conversion of 12/1000, let's briefly review the fundamental concepts of fractions and decimals.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into.
-
Decimals: A decimal is another way to represent a part of a whole. It uses a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
Converting 12/1000 to a Decimal:
The most straightforward way to convert 12/1000 to a decimal is by performing the division: dividing the numerator (12) by the denominator (1000).
12 ÷ 1000 = 0.012
Therefore, 12/1000 as a decimal is 0.012.
Understanding the Place Value:
Let's break down the decimal 0.012 to understand its place value:
- 0: Represents the whole number part (there are no whole numbers).
- 0: Represents the tenths place (zero tenths).
- 1: Represents the hundredths place (one hundredth).
- 2: Represents the thousandths place (two thousandths).
This clearly shows that 0.012 is twelve thousandths.
Alternative Methods for Conversion:
While direct division is the most common method, there are alternative approaches, particularly useful for understanding the underlying principles and handling more complex fractions.
Method 1: Using Equivalent Fractions:
We can convert the fraction to an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). While this is already a power of 10 in this case, this method is beneficial for understanding the process. Since the denominator is already 1000, we can directly write the decimal.
Method 2: Understanding Decimal Place Values Directly:
By understanding that the denominator represents the place value, we can directly write the decimal. Since the denominator is 1000, we know the last digit will be in the thousandths place. Therefore, we can write 12 as 0.012 to represent twelve thousandths.
Method 3: Using Long Division (For More Complex Fractions):
For more complex fractions where direct division might be challenging, long division offers a systematic approach. However, for 12/1000, direct division is much simpler.
Practical Applications of Decimal Conversions:
Converting fractions to decimals is essential in various real-world scenarios:
-
Finance: Calculating percentages, interest rates, and discounts often involve decimal conversions. For example, understanding 0.012 as a decimal equivalent of 12/1000 is crucial in financial calculations.
-
Measurement: Many measurements involve fractions (e.g., inches, centimeters), which are often converted to decimals for easier calculations and comparisons. Understanding the decimal equivalent is vital for precision.
-
Science: Scientific data frequently involves fractions that need to be converted to decimals for analysis and calculations. This is particularly true in fields like chemistry and physics.
-
Engineering: Engineering designs and calculations frequently require decimal precision, making fraction-to-decimal conversion a necessary skill.
-
Everyday Life: From calculating tips to sharing portions of food, understanding decimals helps us manage various aspects of daily life more efficiently.
Expanding on Decimal Concepts:
Understanding the concept of decimals extends beyond simple conversions. Let's explore some related concepts:
-
Rounding Decimals: Sometimes, we need to round decimals to a specific number of decimal places. For instance, 0.012 rounded to one decimal place would be 0.0. Rounding is essential for simplifying numbers and presenting data concisely.
-
Adding and Subtracting Decimals: Performing arithmetic operations on decimals involves aligning the decimal points and performing the operations as you would with whole numbers. The same principles apply to adding and subtracting fractions as well.
-
Multiplying and Dividing Decimals: Multiplying decimals involves multiplying the numbers as whole numbers and then placing the decimal point based on the total number of decimal places in the original numbers. Dividing decimals involves adjusting the decimal points to make the divisor a whole number before performing the division.
-
Comparing Decimals: Comparing decimals involves comparing the digits starting from the leftmost digit. The decimal with the larger digit in the highest place value is the larger decimal.
-
Converting Decimals to Fractions: Conversely, you can convert decimals to fractions by writing the decimal as a fraction with a denominator that is a power of 10. This is the reverse process of what we've done above. For example, 0.012 can be written as 12/1000. This process can then be further simplified by finding the greatest common divisor (GCD) of the numerator and denominator.
Advanced Applications and Further Learning:
The conversion of fractions to decimals is a building block for more complex mathematical concepts:
-
Scientific Notation: Very large or very small numbers are often expressed in scientific notation, which uses decimals and powers of 10.
-
Algebra: Solving algebraic equations often involves working with decimals and fractions.
-
Calculus: Calculus utilizes decimals and fractions extensively in its various applications, from differentiation to integration.
Conclusion:
Converting 12/1000 to its decimal equivalent, 0.012, is a relatively straightforward process. However, understanding the underlying principles of fractions, decimals, and the various methods for conversion is crucial for tackling more complex problems. This comprehensive guide has covered the basics, provided alternative methods, and highlighted the real-world applications of this fundamental mathematical skill. Mastering this skill opens doors to deeper mathematical understanding and broader applications across various fields. Remember to practice regularly and explore further learning resources to solidify your understanding and build confidence in tackling numerical challenges.
Latest Posts
Latest Posts
-
According To Sociologists Doctors Are
Sep 13, 2025
-
Multiplier For 10 Degree Offset
Sep 13, 2025
-
Hybridization Of Br In Bro
Sep 13, 2025
-
Gcf Of 26 And 39
Sep 13, 2025
-
What Were The Three Reasons
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 12 1000 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.