15 18 In Lowest Terms.
gasmanvison
Sep 10, 2025 · 5 min read
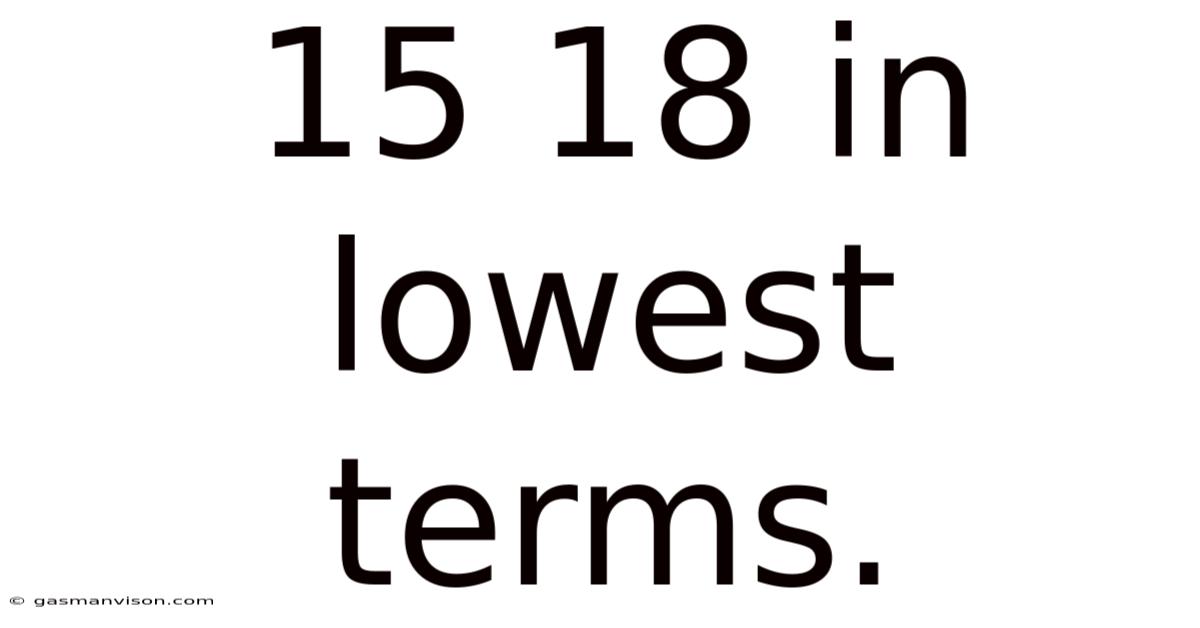
Table of Contents
Simplifying Fractions: A Deep Dive into 15/18 in Lowest Terms
This article explores the simplification of the fraction 15/18, providing a comprehensive understanding of the process and its underlying mathematical principles. We'll go beyond just finding the answer, delving into the concepts of greatest common divisors, prime factorization, and the importance of simplifying fractions in various mathematical contexts. This explanation is designed to be helpful for students learning about fractions for the first time, as well as those seeking a more robust understanding of the topic.
Meta Description: Learn how to simplify the fraction 15/18 to its lowest terms. This detailed guide explains the process step-by-step, covering greatest common divisors, prime factorization, and the importance of simplifying fractions in mathematics.
What does it mean to simplify a fraction?
Simplifying a fraction means reducing it to its simplest form, where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. This process doesn't change the value of the fraction; it just expresses it in a more concise and manageable way. Think of it like reducing a recipe – you can halve the ingredients, but the final dish will still taste the same. Simplifying 15/18 is precisely this process of finding the equivalent fraction with the smallest possible whole numbers.
Methods for Simplifying 15/18
There are several ways to simplify 15/18, each offering a slightly different approach to understanding the underlying concepts.
1. Finding the Greatest Common Divisor (GCD)
The most direct method involves finding the greatest common divisor (GCD) of the numerator (15) and the denominator (18). The GCD is the largest number that divides both 15 and 18 without leaving a remainder.
-
Listing Factors: One way to find the GCD is by listing the factors of each number.
- Factors of 15: 1, 3, 5, 15
- Factors of 18: 1, 2, 3, 6, 9, 18
The largest number that appears in both lists is 3. Therefore, the GCD of 15 and 18 is 3.
-
Prime Factorization: A more systematic approach involves prime factorization. We break down each number into its prime factors (numbers divisible only by 1 and themselves).
- 15 = 3 x 5
- 18 = 2 x 3 x 3 = 2 x 3²
The common prime factor is 3 (it appears once in the factorization of 15 and twice in the factorization of 18). Therefore, the GCD is 3.
Once we have the GCD, we divide both the numerator and the denominator by it:
15 ÷ 3 = 5 18 ÷ 3 = 6
Therefore, 15/18 simplified to its lowest terms is 5/6.
2. Step-wise Division by Common Factors
This method involves repeatedly dividing the numerator and denominator by common factors until no more common factors remain.
-
Notice that both 15 and 18 are divisible by 3. Divide both by 3:
15 ÷ 3 = 5 18 ÷ 3 = 6
This gives us the fraction 5/6. Since 5 and 6 share no common factors other than 1, the fraction is now in its simplest form.
Therefore, 15/18 simplified is 5/6.
3. Using the Euclidean Algorithm (for larger numbers)
For larger numbers, the Euclidean algorithm provides a more efficient method for finding the GCD. While not strictly necessary for 15/18, understanding this method is beneficial for working with more complex fractions. The algorithm involves repeated division with remainder until the remainder is 0. The last non-zero remainder is the GCD.
Let's illustrate with 15 and 18:
- Divide 18 by 15: 18 = 15 x 1 + 3
- Divide 15 by the remainder (3): 15 = 3 x 5 + 0
The last non-zero remainder is 3, which is the GCD of 15 and 18. We then proceed to divide both the numerator and denominator by 3, as shown in the previous methods, arriving at 5/6.
Why is Simplifying Fractions Important?
Simplifying fractions is crucial for several reasons:
-
Clarity and Understanding: Simplified fractions are easier to understand and visualize. 5/6 is much clearer than 15/18.
-
Easier Calculations: Performing calculations (addition, subtraction, multiplication, and division) with simplified fractions is significantly easier and less prone to errors.
-
Standard Form: Presenting answers in simplified form is a standard practice in mathematics, ensuring consistency and facilitating communication.
-
Real-world Applications: Simplifying fractions has practical applications in various fields, including cooking (adjusting recipes), construction (measuring materials), and finance (calculating proportions).
Expanding on the Concept: Equivalent Fractions
The process of simplifying a fraction highlights the concept of equivalent fractions. 15/18, 5/6, and many other fractions represent the same proportion or value. They are equivalent. Simplifying a fraction simply means finding the most concise representation of that equivalent fraction.
Advanced Considerations: Irrational Numbers and Decimal Representation
While this article focuses on simplifying rational fractions (fractions where both the numerator and denominator are integers), it's important to note that the concept of simplification extends to other types of numbers. For example, simplifying expressions involving irrational numbers (like √2 or π) often involves rationalizing the denominator. Converting a fraction to a decimal representation is another method of expressing the value, but simplification before conversion often leads to a simpler decimal form (e.g., simplifying 15/18 to 5/6 makes the decimal conversion 0.8333... easier to obtain and interpret than converting 15/18 directly).
Conclusion:
Simplifying the fraction 15/18 to its lowest terms, 5/6, is a straightforward process. However, understanding the underlying mathematical principles, such as finding the greatest common divisor through factorization or the Euclidean algorithm, provides a stronger foundation for tackling more complex fraction simplification problems in the future. The ability to simplify fractions is an essential skill in mathematics, with applications extending far beyond the classroom. Mastering this skill enhances understanding, improves calculation efficiency, and contributes to a more robust mathematical foundation. Remember, the key is to find the greatest common divisor and divide both the numerator and denominator by that number. Practice makes perfect; keep working on various fraction simplification exercises to improve your understanding and speed.
Latest Posts
Latest Posts
-
Implicit Instantiation Of Undefined Template
Sep 10, 2025
-
Is Rum Stronger Than Tequila
Sep 10, 2025
-
Kyra Has A Rock Collection
Sep 10, 2025
-
Are Pumice Stones Single Use
Sep 10, 2025
-
A Christmas Story Ralphie Brother
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 15 18 In Lowest Terms. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.