167 118 82 57 41
gasmanvison
Sep 23, 2025 · 5 min read
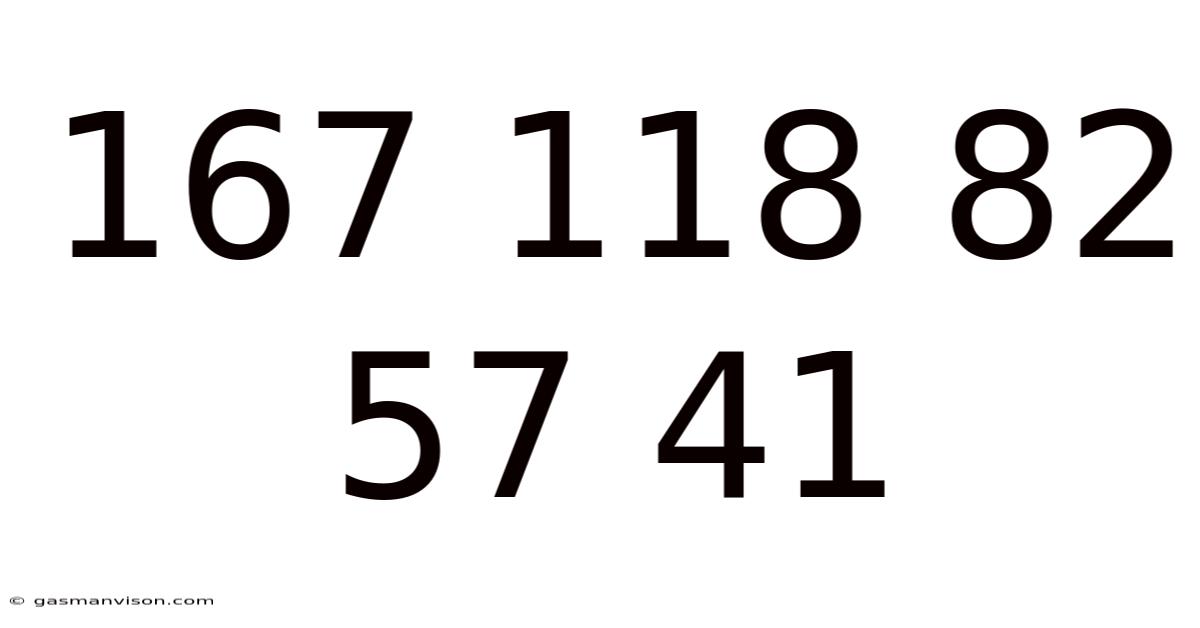
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Pattern-Based Approaches to Understanding 167, 118, 82, 57, 41
This article delves into the intriguing numerical sequence: 167, 118, 82, 57, 41. We'll explore various mathematical and pattern-based approaches to uncover the underlying logic governing this sequence. Understanding these methods not only helps solve this specific puzzle but also provides valuable tools for tackling similar number sequence problems. The goal is to find a formula or rule that can generate the next number in the sequence and potentially predict future numbers.
Understanding Number Sequences: A Primer
Number sequences are a common feature in mathematical puzzles, IQ tests, and programming challenges. They test your ability to identify patterns, make logical deductions, and apply mathematical principles. Solving a number sequence involves identifying the relationship between consecutive numbers. This relationship could be anything from simple addition or subtraction to more complex operations involving exponents, prime numbers, or even Fibonacci sequences.
Analyzing the Given Sequence: 167, 118, 82, 57, 41
Let's systematically analyze the sequence 167, 118, 82, 57, 41. Our analysis will explore several potential approaches:
1. Difference Analysis: This is a fundamental method where we examine the differences between consecutive numbers in the sequence.
- 167 - 118 = 49
- 118 - 82 = 36
- 82 - 57 = 25
- 57 - 41 = 16
Notice a pattern emerging in the differences: 49, 36, 25, 16. These are perfect squares: 7², 6², 5², 4². This suggests a strong pattern. The next difference should be 3² = 9. Therefore, the next number in the sequence would be 41 - 9 = 32.
2. Quadratic Formula Approach: Since the second differences (differences of the differences) are constant, this implies a quadratic relationship. We can use this information to derive a quadratic formula that generates the sequence.
Let's assume the formula is of the form: an² + bn + c, where 'n' represents the position of the number in the sequence (n=1, 2, 3, 4, 5...).
We can set up a system of equations using the first three numbers:
- For n=1: a + b + c = 167
- For n=2: 4a + 2b + c = 118
- For n=3: 9a + 3b + c = 82
Solving this system of equations (using substitution or matrix methods) will yield the values of a, b, and c. This will give us a quadratic formula that can generate the entire sequence and predict future numbers. While the calculations are involved, this method offers a rigorous mathematical approach to confirming the pattern identified through difference analysis.
3. Analyzing the Digits: Another approach involves looking at the individual digits of each number in the sequence. This method is often more exploratory and may not always yield a clear pattern, but it's worth investigating. In this case, a straightforward digit-based pattern is not immediately apparent.
4. Prime Number Relationship (Less Likely): While less obvious, we can explore whether prime numbers or their properties play a role. Checking the prime factorization of each number might reveal a hidden pattern. However, in this instance, this approach doesn't immediately yield a clear relationship.
5. Recursive Relationships: A recursive relationship defines a term based on preceding terms. While the differences analysis hints at a recursive pattern, we haven't explicitly defined a recursive formula. A recursive approach could be explored to formalize the pattern.
Verifying the Pattern and Predicting Future Numbers:
Based on the difference analysis and the observation of perfect squares, we've determined a strong pattern. The next difference should be 3² = 9. Therefore, the next number in the sequence is 41 - 9 = 32.
Using the quadratic formula approach (solving the system of equations), we would confirm or refute this finding with a more rigorous mathematical approach. This method would allow us to generate not only the next number but also numbers further down the sequence with a high degree of confidence.
Expanding the Analysis: Beyond the Immediate Solution
While finding the next number (32) is a satisfying result, the real value lies in understanding the underlying mathematical principles and developing a general approach to solve similar problems. Here's how we can expand our analysis:
a) Exploring Alternative Patterns: It's essential to acknowledge that multiple patterns might exist. While the difference analysis leading to perfect squares is a strong candidate, it's always possible another, equally valid, pattern could be found. Thorough exploration of different methods is crucial.
b) Using Software and Programming: For more complex sequences, using software like MATLAB, Python (with libraries like NumPy), or other mathematical software packages can significantly aid in analyzing the data and identifying patterns. These tools can handle large datasets, perform complex calculations (like solving systems of equations), and visualize the data in ways that reveal hidden patterns.
c) The Importance of Data Visualization: Visualizing the sequence (e.g., plotting it on a graph) can help reveal patterns that might be missed by purely numerical analysis. The graph can show whether the sequence is linear, quadratic, exponential, or follows some other function.
d) Extending the Sequence: Once a reliable pattern is established, we can confidently extend the sequence. Using the quadratic formula or the recursive relationship derived from our analysis, we can predict future numbers in the sequence with a high degree of accuracy.
Conclusion: The Power of Pattern Recognition and Mathematical Reasoning
Solving number sequences like 167, 118, 82, 57, 41 requires a combination of pattern recognition, mathematical reasoning, and methodical analysis. While difference analysis provided a straightforward approach in this instance, other methods, including the quadratic formula approach, offered a more rigorous mathematical validation. The key takeaway is not just finding the solution (32 in this case) but gaining a deeper understanding of the mathematical principles and developing a versatile toolkit for tackling similar numerical challenges. Remember, perseverance, a systematic approach, and the ability to explore multiple avenues are essential for success in solving these types of puzzles. The more diverse your approaches are, the more likely you are to uncover the underlying pattern and gain a complete understanding of the sequence.
Latest Posts
Latest Posts
-
1 4 X 12 2
Sep 24, 2025
-
Wagon Train At Dusk Summary
Sep 24, 2025
-
Different Categories Of R Groups
Sep 24, 2025
-
What Does This Graph Demonstrate
Sep 24, 2025
-
Contrast Environmental Science And Ecology
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 167 118 82 57 41 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.