2 1/2 Divided By 1/2
gasmanvison
Sep 13, 2025 · 5 min read
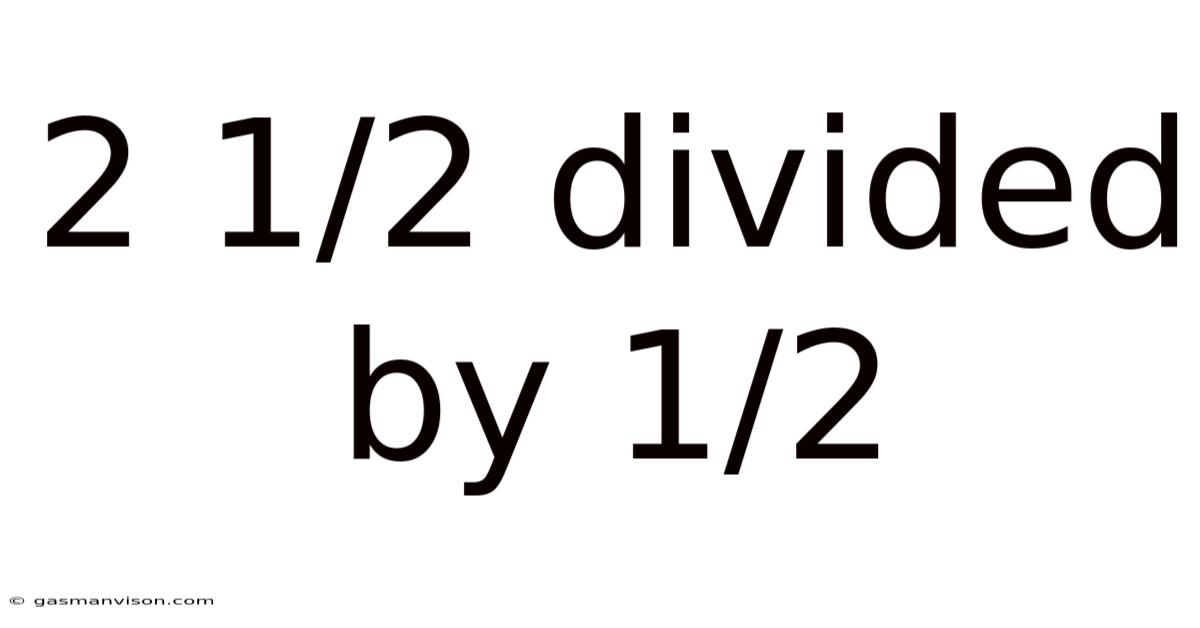
Table of Contents
2 1/2 Divided by 1/2: A Deep Dive into Fraction Division
This article explores the seemingly simple problem of 2 1/2 divided by 1/2, delving beyond the basic answer to understand the underlying concepts, explore different solution methods, and demonstrate the practical applications of fraction division. We'll cover various approaches, including converting mixed numbers to improper fractions, using reciprocals, and visualizing the problem using real-world examples. By the end, you'll not only know the answer but also possess a solid grasp of the principles involved, making you confident in tackling similar fraction division problems.
Understanding the Problem: 2 1/2 ÷ 1/2
The problem, 2 1/2 divided by 1/2, asks: how many times does 1/2 fit into 2 1/2? This seemingly simple question highlights a crucial aspect of division: it represents repeated subtraction or the process of finding how many groups of a certain size can be made from a larger quantity.
Method 1: Converting to Improper Fractions
The most common and efficient method involves converting the mixed number (2 1/2) into an improper fraction. Remember, a mixed number combines a whole number and a fraction, while an improper fraction has a numerator larger than its denominator.
-
Step 1: Convert the mixed number: To convert 2 1/2 to an improper fraction, we multiply the whole number (2) by the denominator (2) and add the numerator (1). This result (5) becomes the new numerator, while the denominator remains the same (2). Therefore, 2 1/2 becomes 5/2.
-
Step 2: Rewrite the division problem: Our problem now becomes 5/2 ÷ 1/2.
-
Step 3: Invert and Multiply: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/2 is 2/1 (or simply 2). So, we rewrite the problem as (5/2) x (2/1).
-
Step 4: Simplify and Solve: Multiply the numerators together (5 x 2 = 10) and the denominators together (2 x 1 = 2). This gives us 10/2.
-
Step 5: Simplify to a whole number: Finally, simplify the improper fraction 10/2 by dividing the numerator by the denominator: 10 ÷ 2 = 5.
Therefore, 2 1/2 divided by 1/2 equals 5.
Method 2: Visual Representation
Visualizing the problem can be incredibly helpful, especially for beginners. Imagine you have 2 1/2 pizzas. Each serving is 1/2 a pizza. How many servings do you have?
You can easily see that there are two whole pizzas, each containing two 1/2 pizza servings (2 x 2 = 4 servings). The remaining half-pizza contains one more serving (1 serving). Adding those together (4 + 1 = 5), we get the same answer: 5 servings. This visual method helps solidify the understanding of fraction division in a concrete way.
Method 3: Using Decimal Equivalents
Another approach is to convert the fractions to decimals and then perform the division.
-
Step 1: Convert to decimals: 2 1/2 is equivalent to 2.5, and 1/2 is equivalent to 0.5.
-
Step 2: Perform decimal division: Divide 2.5 by 0.5: 2.5 ÷ 0.5 = 5.
This method provides an alternative way to arrive at the same answer, highlighting the relationship between fractions and decimals. However, it's important to note that this method might not be as efficient or accurate when dealing with complex fractions.
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life. Consider these examples:
-
Cooking: A recipe calls for 1/2 cup of flour per serving. You have 2 1/2 cups of flour. How many servings can you make? (2 1/2 ÷ 1/2 = 5 servings)
-
Sewing: You need 1/2 yard of fabric for each project. You have 2 1/2 yards of fabric. How many projects can you complete? (2 1/2 ÷ 1/2 = 5 projects)
-
Construction: You need 1/2 a bag of cement for each section of a wall. You have 2 1/2 bags of cement. How many sections of the wall can you build? (2 1/2 ÷ 1/2 = 5 sections)
These examples demonstrate how fraction division is essential for accurately measuring and allocating resources in various practical scenarios.
Expanding the Concept: More Complex Fraction Division
While we've focused on 2 1/2 ÷ 1/2, the principles discussed can be applied to more complex fraction division problems. The key is to always follow these steps:
-
Convert mixed numbers to improper fractions: This simplifies the problem and makes calculations easier.
-
Invert and multiply: This is the core principle of dividing fractions.
-
Simplify: Reduce the resulting fraction to its lowest terms or convert it to a whole number or mixed number if possible.
For example, let's consider 3 2/3 ÷ 1/4:
-
Convert 3 2/3 to an improper fraction: (3 x 3 + 2)/3 = 11/3
-
Invert and multiply: (11/3) x (4/1) = 44/3
-
Simplify: 44/3 = 14 2/3
This demonstrates the versatility and power of this method in solving various fraction division problems.
Troubleshooting Common Mistakes
Several common mistakes can arise when dealing with fraction division:
-
Forgetting to invert and multiply: This is a crucial step; failing to do so will lead to an incorrect answer.
-
Incorrect conversion of mixed numbers: Errors in converting mixed numbers to improper fractions will propagate through the calculation.
-
Improper simplification: Failing to simplify the resulting fraction can leave the answer in a cumbersome form.
Careful attention to each step is essential to avoid these errors and achieve accurate results.
Conclusion: Mastering Fraction Division
Understanding fraction division is fundamental to mathematical proficiency. The problem 2 1/2 ÷ 1/2, while seemingly simple, serves as an excellent foundation for grasping the underlying principles. Through the various methods explored – converting to improper fractions, visual representation, and using decimal equivalents – we've demonstrated that the answer is consistently 5. This understanding, combined with the ability to apply these techniques to more complex problems, empowers individuals to confidently tackle fraction division in various academic and real-world contexts. Remember to practice regularly, and don't hesitate to visualize the problem to deepen your understanding. By mastering these techniques, you’ll enhance your mathematical skills and increase your problem-solving capabilities.
Latest Posts
Latest Posts
-
Actual Dimensions Of A 2x6
Sep 13, 2025
-
Streams And Rivers Distinguishing Characteristics
Sep 13, 2025
-
Is Koh A Strong Base
Sep 13, 2025
-
How Many Lbs Is 500kg
Sep 13, 2025
-
Left Ankle Pain Icd 10
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 2 1/2 Divided By 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.