2 1/3 + 3 1/3
gasmanvison
Sep 24, 2025 · 6 min read
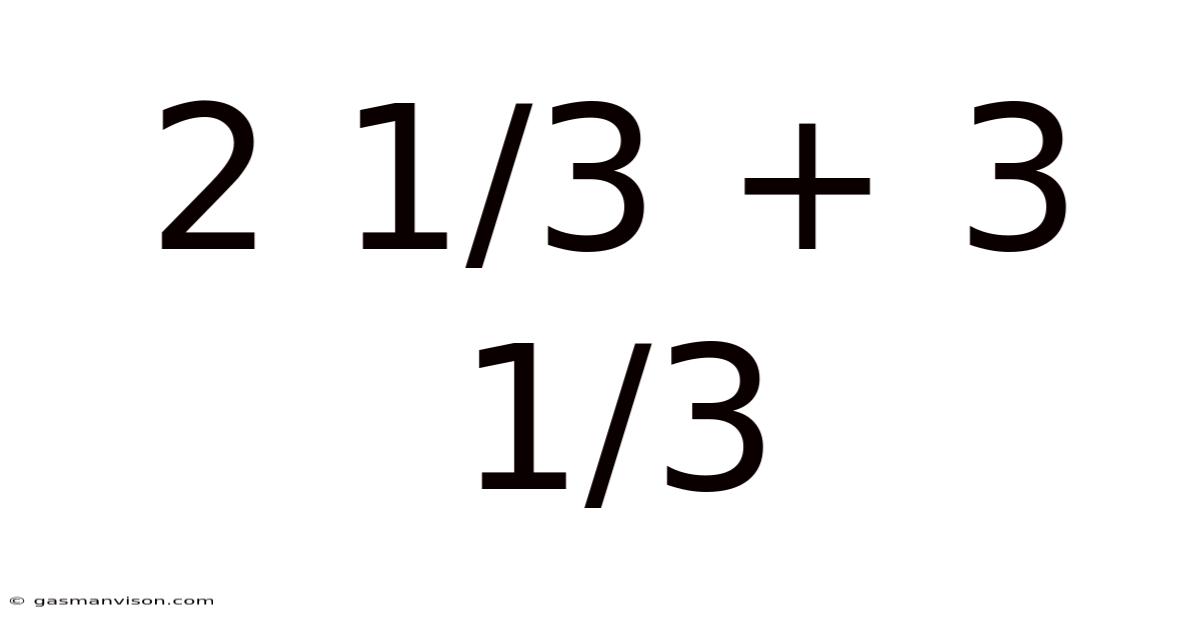
Table of Contents
Decoding 2 1/3 + 3 1/3: A Deep Dive into Mixed Number Addition
This article delves into the seemingly simple addition problem of 2 1/3 + 3 1/3, exploring not just the solution but also the underlying mathematical concepts, different approaches to solving it, and the broader implications for understanding fractions and mixed numbers. We'll cover various methods, from the traditional approach to more visual representations, making this a comprehensive guide for anyone wanting to master this fundamental arithmetic skill. This understanding extends beyond basic arithmetic; it forms the foundation for more complex algebraic manipulations and problem-solving in higher-level mathematics.
Understanding Mixed Numbers and Fractions
Before diving into the addition, let's solidify our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 2 1/3. This represents two whole units and one-third of another unit. A fraction, on the other hand, represents a part of a whole, expressed as a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. In 1/3, the whole is divided into three equal parts, and we're considering one of those parts.
Method 1: The Traditional Approach
The most common method for adding mixed numbers involves dealing with the whole numbers and fractions separately.
-
Add the Whole Numbers: Add the whole numbers together: 2 + 3 = 5.
-
Add the Fractions: Add the fractions together: 1/3 + 1/3 = 2/3.
-
Combine the Results: Combine the sum of the whole numbers and the sum of the fractions: 5 + 2/3 = 5 2/3.
Therefore, 2 1/3 + 3 1/3 = 5 2/3. This method is straightforward and efficient for simple additions.
Method 2: Converting to Improper Fractions
Another approach involves converting the mixed numbers into improper fractions before adding. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert to Improper Fractions:
- To convert 2 1/3 to an improper fraction, multiply the whole number (2) by the denominator (3), add the numerator (1), and keep the same denominator: (2 * 3) + 1 = 7, so 2 1/3 becomes 7/3.
- Similarly, 3 1/3 becomes (3 * 3) + 1 = 10/3.
-
Add the Improper Fractions: Add the improper fractions together: 7/3 + 10/3 = 17/3.
-
Convert Back to a Mixed Number: Convert the improper fraction 17/3 back to a mixed number by dividing the numerator (17) by the denominator (3): 17 ÷ 3 = 5 with a remainder of 2. This means 17/3 is equal to 5 2/3.
Therefore, 2 1/3 + 3 1/3 = 5 2/3. This method is particularly useful when dealing with more complex mixed number additions or when performing other operations with fractions.
Method 3: Visual Representation using Fraction Bars
Visual aids can significantly enhance understanding, especially for those who struggle with abstract mathematical concepts. Using fraction bars or diagrams can provide a concrete representation of the addition.
Imagine two fraction bars representing 2 1/3. Each bar is divided into three equal sections, with two bars completely filled and one-third of the third bar filled. Then, add three more fraction bars representing 3 1/3, similarly divided. Combining all the filled sections, we have five whole bars completely filled and two-thirds of another bar. This visually demonstrates that 2 1/3 + 3 1/3 = 5 2/3.
Method 4: Using a Number Line
A number line provides another visual method for understanding the addition. Start at 2 1/3 on the number line. Then, move 3 1/3 units to the right. The point you land on will be the sum, which is 5 2/3. This approach is particularly helpful for visualizing the magnitude of the addition.
Real-World Applications
Understanding mixed number addition isn't just about abstract mathematical concepts; it has numerous practical applications in daily life. Consider these examples:
- Baking: If a recipe calls for 2 1/3 cups of flour and 3 1/3 cups of sugar, you'll need to add these quantities to determine the total amount of dry ingredients.
- Construction: Measuring lengths of wood or other materials often involves working with mixed numbers, and accurate addition is crucial for precise measurements.
- Sewing: Calculating fabric requirements for a project involves adding mixed numbers representing different lengths of fabric pieces.
- Cooking: Many recipes rely on precise measurements involving fractions and mixed numbers.
Extending the Concept: Adding More Than Two Mixed Numbers
The principles discussed above can be extended to add more than two mixed numbers. The key is to either add the whole numbers and fractions separately or convert all mixed numbers to improper fractions, perform the addition, and then convert back to a mixed number. For example, to add 1 1/3 + 2 2/3 + 3 1/3, you could add the whole numbers (1 + 2 + 3 = 6) and the fractions (1/3 + 2/3 + 1/3 = 4/3 = 1 1/3), resulting in 6 + 1 1/3 = 7 1/3. Alternatively, convert each to an improper fraction (4/3 + 8/3 + 10/3 = 22/3), then convert back to 7 1/3.
Troubleshooting Common Mistakes
Several common errors can occur when adding mixed numbers:
- Forgetting to convert to improper fractions: When dealing with more complex problems or those involving different denominators, converting to improper fractions is essential for accurate results.
- Incorrectly adding the fractions: Ensure that you add the numerators correctly while keeping the denominator the same (provided the denominators are already the same). If not, find a common denominator before addition.
- Not simplifying the final answer: Always simplify your answer to its lowest terms, converting improper fractions to mixed numbers.
Conclusion: Mastering Mixed Number Addition
Adding mixed numbers like 2 1/3 + 3 1/3, while seemingly simple, provides a foundational understanding of fractions, mixed numbers, and arithmetic operations. Mastering this skill is essential for success in mathematics and its various applications in real-world scenarios. By understanding the different methods and avoiding common mistakes, you can confidently tackle these and more complex problems. The methods presented here—traditional approach, conversion to improper fractions, visual representation, and number line—offer multiple pathways to understanding and mastering this crucial skill. Remember that consistent practice and a clear understanding of the underlying concepts are key to achieving proficiency. Don't hesitate to use visual aids and explore different approaches until you find the method that works best for you.
Latest Posts
Latest Posts
-
Partial Charges Occur When
Sep 24, 2025
-
Sternbergs Triangular Theory Of Love
Sep 24, 2025
-
Advanced Maternal Age Icd 10
Sep 24, 2025
-
Why Does Mercutio Fight Tybalt
Sep 24, 2025
-
5 Ft 6 To Cm
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 1/3 + 3 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.