2 2/3 As A Decimal
gasmanvison
Sep 03, 2025 · 5 min read
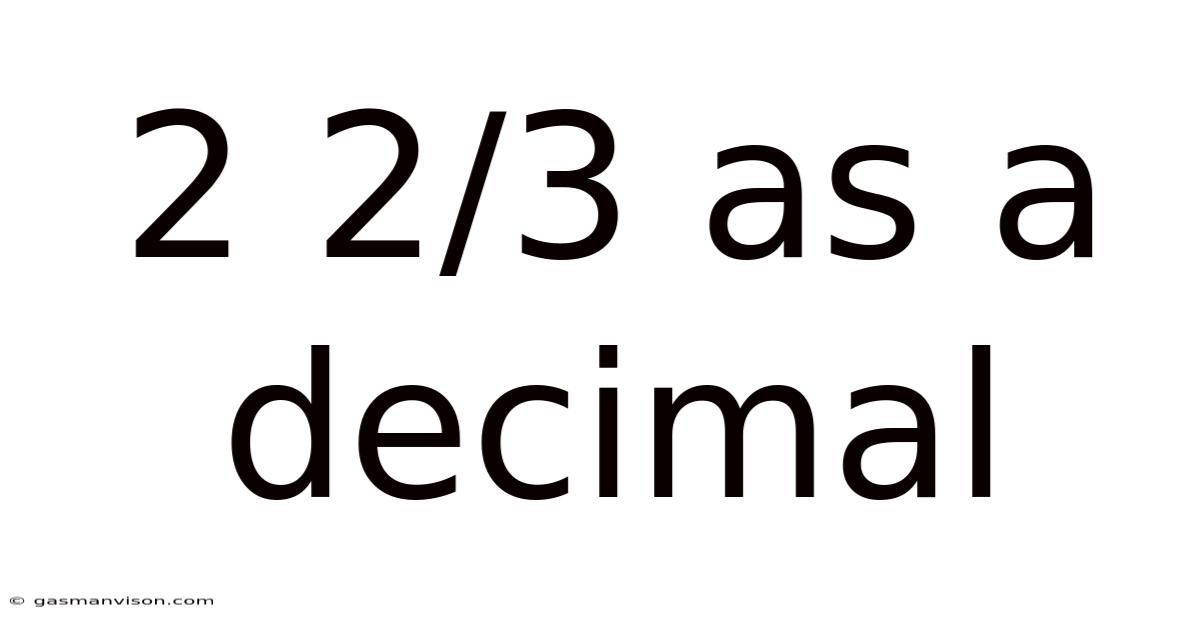
Table of Contents
2 2/3 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, frequently encountered in various fields from everyday calculations to advanced scientific applications. This article delves deep into the conversion of the mixed number 2 2/3 into its decimal equivalent, exploring multiple methods, highlighting common pitfalls, and providing a broader understanding of fraction-to-decimal conversion. Understanding this seemingly simple conversion lays a strong foundation for more complex mathematical operations.
Understanding Mixed Numbers and Fractions
Before we embark on the conversion process, let's briefly review the components of a mixed number like 2 2/3. A mixed number combines a whole number (2 in this case) and a proper fraction (2/3). The proper fraction indicates a portion less than one. To convert this into a decimal, we need to express the entire quantity as a single fraction, then divide the numerator by the denominator.
Method 1: Converting the Mixed Number to an Improper Fraction
This is the most common and generally preferred method. It involves converting the mixed number into an improper fraction—a fraction where the numerator is larger than the denominator. Here's how:
- Multiply the whole number by the denominator: 2 * 3 = 6
- Add the result to the numerator: 6 + 2 = 8
- Keep the same denominator: The denominator remains 3.
Therefore, 2 2/3 becomes the improper fraction 8/3.
Method 2: Converting the Whole Number and Fraction Separately
This method involves handling the whole number and the fraction separately before combining the results. It provides a slightly different perspective on the conversion process.
- Convert the fraction to a decimal: Divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.666666... (This is a repeating decimal)
- Add the whole number: Add the whole number (2) to the decimal value obtained in step 1: 2 + 0.666666... = 2.666666...
This method provides the same result as the first method, albeit through a different approach.
Method 3: Long Division
Long division offers a more hands-on approach to converting the improper fraction 8/3 into a decimal. This method is particularly useful for understanding the underlying process of division and for dealing with fractions that might not be easily recognizable as decimal equivalents.
- Set up the long division: Place the numerator (8) inside the division symbol and the denominator (3) outside.
- Perform the division: Divide 8 by 3. 3 goes into 8 twice (3 x 2 = 6), leaving a remainder of 2.
- Add a decimal point and a zero: Add a decimal point after the 2 in the quotient and a zero to the remainder. Now you're dividing 20 by 3.
- Continue the division: 3 goes into 20 six times (3 x 6 = 18), leaving a remainder of 2.
- Repeat the process: You will notice that the remainder is always 2, resulting in a repeating decimal of 0.6666...
- Combine the whole number: Remember the whole number from the original mixed number (2). Combine this with the decimal result: 2 + 0.6666... = 2.6666...
Understanding Repeating Decimals
The decimal representation of 2 2/3 is a recurring or repeating decimal, denoted by 2.6̅6̅ or 2.666... The bar over the 6 indicates that the digit 6 repeats infinitely. This is a crucial aspect of understanding the result. In many practical applications, it's sufficient to round the decimal to a specific number of decimal places, such as 2.67. However, it's important to remember that the precise value is a non-terminating repeating decimal.
Practical Applications and Rounding
The decimal representation of 2 2/3 finds application in numerous contexts. Consider the following scenarios:
- Measurements: If you're measuring something and obtain a length of 2 2/3 meters, you might round it to 2.67 meters for practical purposes.
- Financial Calculations: In financial calculations, the precision required might necessitate using the full repeating decimal or rounding to several decimal places depending on the currency and the level of accuracy needed.
- Scientific Computations: Scientific computations may require retaining the full precision or using specialized techniques to handle repeating decimals.
Common Mistakes and How to Avoid Them
Several common errors can occur during fraction-to-decimal conversion:
- Incorrectly converting the mixed number to an improper fraction: Carefully follow the steps outlined above to avoid errors in this crucial step. Double-check your calculations.
- Misinterpreting the repeating decimal: Understand that the repeating 6 in 2.666... continues infinitely. Rounding should be done consciously and with an understanding of the implications.
- Ignoring the whole number: Don't forget to add the whole number back to the decimal representation after converting the fraction.
Expanding on Decimal Conversion Techniques
The conversion of 2 2/3 provides a foundation for understanding more complex conversions. Consider these related concepts:
- Converting other mixed numbers: The same principles apply to converting any mixed number to a decimal.
- Converting improper fractions: The long division method is especially useful for converting improper fractions, even those with larger numerators and denominators.
- Working with decimals in different number systems: While we focus on the decimal system (base 10), these principles can extend to other number systems, such as binary (base 2) or hexadecimal (base 16).
- Understanding the relationship between fractions and decimals: The ability to seamlessly convert between fractions and decimals is a critical skill for higher-level mathematical concepts.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting 2 2/3 to its decimal equivalent, approximately 2.666..., is more than just a simple mathematical exercise. It highlights the fundamental relationship between fractions and decimals and provides a stepping stone to understanding more advanced mathematical concepts. By mastering this conversion, along with understanding the nuances of repeating decimals and the importance of accuracy and rounding, you build a strong foundation for success in various mathematical and scientific endeavors. Remember the importance of careful calculation and understanding the underlying principles to avoid common errors. The ability to confidently navigate these conversions is a valuable asset in numerous academic and practical applications.
Latest Posts
Latest Posts
-
1 4 Mile To Feet
Sep 03, 2025
-
Molar Mass Of Sulfuric Acid
Sep 03, 2025
-
What Does M S D S Stand For
Sep 03, 2025
-
Is Nad To Nadh Exergonic
Sep 03, 2025
-
Ir Spectra Of Methyl Benzoate
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about 2 2/3 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.