2 3/7 - 5 6/7
gasmanvison
Sep 11, 2025 · 5 min read
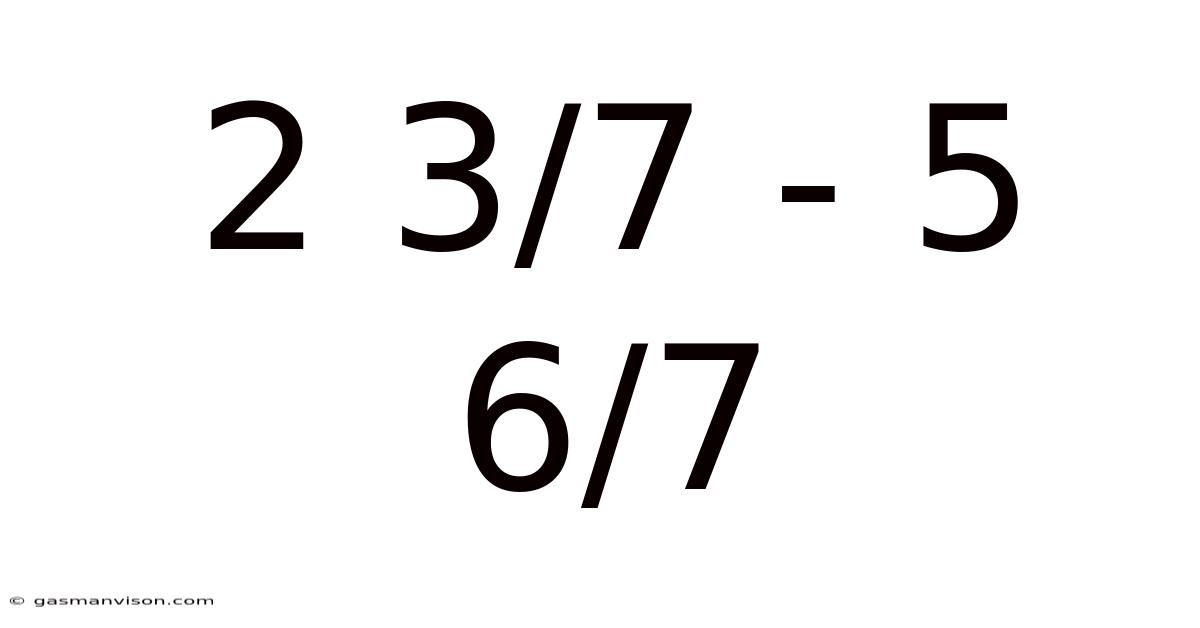
Table of Contents
Solving the Subtraction Problem: 2 3/7 - 5 6/7 A Deep Dive into Fraction Subtraction
This article will comprehensively guide you through solving the subtraction problem 2 3/7 - 5 6/7, explaining the process step-by-step and exploring related concepts in fraction arithmetic. We'll delve into the intricacies of subtracting mixed numbers, borrowing from whole numbers, and simplifying fractions, ultimately equipping you with a thorough understanding of this seemingly simple yet fundamental mathematical operation. This detailed approach will not only help you solve this specific problem but also build a strong foundation for tackling more complex fraction problems in the future.
Understanding Mixed Numbers and Improper Fractions
Before diving into the subtraction, let's refresh our understanding of mixed numbers and improper fractions. A mixed number combines a whole number and a fraction (e.g., 2 3/7). An improper fraction has a numerator larger than or equal to its denominator (e.g., 17/7). These two representations are interchangeable. To convert a mixed number into an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 2 3/7 becomes (2 * 7) + 3 / 7 = 17/7. Conversely, to convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator remains the same.
The Challenge: Subtracting Larger Fractions from Smaller Fractions
The problem 2 3/7 - 5 6/7 presents a unique challenge. We're attempting to subtract a larger mixed number (5 6/7) from a smaller mixed number (2 3/7). This necessitates a crucial step: borrowing.
The Borrowing Process: A Step-by-Step Explanation
Since we can't directly subtract 6/7 from 3/7, we need to borrow from the whole number part of 2 3/7. Here's a breakdown:
-
Borrowing from the Whole Number: We borrow 1 from the whole number 2, leaving us with 1.
-
Converting the Borrowed 1: This borrowed 1 is then converted into a fraction with the same denominator as the existing fractions (7/7).
-
Combining Fractions: Now we have 1 + 3/7 which equals 10/7. This combines the borrowed 1 with the 3/7 from the original mixed number.
-
Rewriting the Equation: Our equation now becomes 10/7 - 5 6/7. We can rewrite 5 6/7 as an improper fraction: (5 * 7) + 6 / 7 = 41/7
-
Subtracting the Improper Fractions: We are now left with a standard subtraction problem of improper fractions: 10/7 - 41/7.
Understanding the Result: Negative Fractions
When we subtract 41/7 from 10/7, we arrive at -31/7. This is a negative improper fraction, indicating that the result of the original subtraction problem is negative.
Converting the Result Back to a Mixed Number
While -31/7 is a correct answer, it's often more convenient to express it as a mixed number. We divide the numerator (-31) by the denominator (7).
-31 ÷ 7 = -4 with a remainder of -3.
Therefore, -31/7 can be expressed as the mixed number -4 3/7.
The Complete Solution: 2 3/7 - 5 6/7 = -4 3/7
Thus, the solution to the subtraction problem 2 3/7 - 5 6/7 is -4 3/7.
Practical Applications and Real-World Scenarios
Understanding fraction subtraction, particularly involving mixed numbers and borrowing, is crucial in various real-world scenarios. Consider these examples:
-
Cooking and Baking: Adjusting recipes often requires subtracting fractions of ingredients. For example, if a recipe calls for 2 3/7 cups of flour but you only have 5 6/7 cups, you can use fraction subtraction to determine how much flour you need to purchase.
-
Finance and Budgeting: Managing finances often involves precise calculations with fractions. Suppose you have $2 3/7 and you need to pay a bill of $5 6/7, fraction subtraction can help you determine the amount you're short.
-
Construction and Measurement: In construction, accurate measurements are paramount. Subtracting fractional lengths of materials is necessary to determine how much material is needed for a project. If a project requires 2 3/7 meters of wood, and you have 5 6/7 meters, determining the excess wood involves the same principles of subtraction.
-
Data Analysis: In statistical analysis and data science, understanding operations with fractions is crucial for various calculations. For instance, when dealing with proportions or percentages, fraction arithmetic is unavoidable.
-
Time Management: While often dealing with decimals for precision, working with time durations frequently utilizes fractions of an hour or minutes. Calculating time differences sometimes requires using fraction subtraction.
Expanding Your Knowledge: Further Exploration of Fractions
While this article focuses on subtraction, understanding other operations with fractions is equally important:
-
Addition of Fractions: Similar to subtraction, adding fractions requires finding a common denominator, adding the numerators, and simplifying the result.
-
Multiplication of Fractions: Multiplying fractions is simpler, as you multiply the numerators and denominators directly.
-
Division of Fractions: Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Mastering these operations strengthens your mathematical abilities and opens up opportunities for tackling more complex mathematical problems encountered in various fields.
Conclusion: Mastering Fraction Subtraction for Success
This comprehensive guide has walked you through solving the problem 2 3/7 - 5 6/7, highlighting the critical steps involved in borrowing and subtracting mixed numbers. Understanding these concepts is fundamental to progressing in mathematics and applying these skills to various practical applications. Remember to practice regularly to solidify your understanding and build confidence in handling fraction problems of all complexities. The ability to manipulate fractions accurately is a valuable skill that will serve you well in many areas of life. By understanding the underlying principles and consistently practicing, you'll confidently tackle any fraction subtraction problem you encounter. This detailed walkthrough provides not only the solution but also builds a strong understanding of the core concepts, ensuring future success with more challenging problems.
Latest Posts
Latest Posts
-
Typical Radius Of Lysozyme Protein
Sep 11, 2025
-
Convert 21 C To Fahrenheit
Sep 11, 2025
-
Find The Length Of Ce
Sep 11, 2025
-
14 Kg How Many Pounds
Sep 11, 2025
-
Lewis Dot Structure For Ch2br2
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 2 3/7 - 5 6/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.