2 Copies Of 1/10 Is
gasmanvison
Sep 15, 2025 · 5 min read
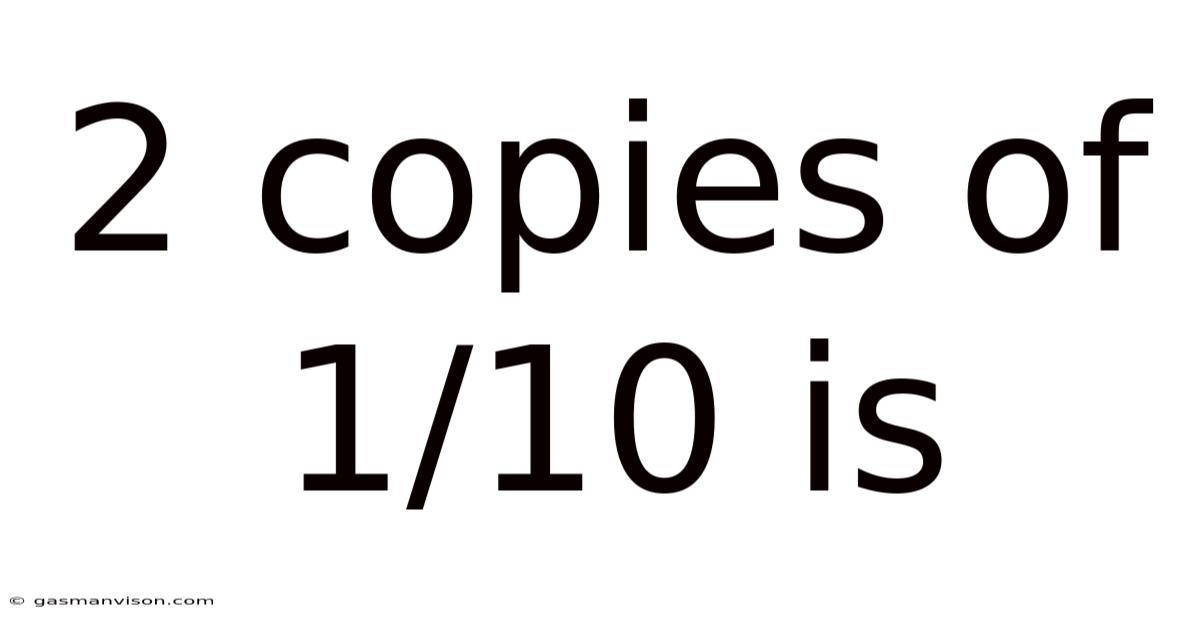
Table of Contents
2 Copies of 1/10 Is: Exploring Fractions, Duplication, and Their Applications
This article delves into the seemingly simple question, "2 copies of 1/10 is...?" While the answer might seem immediately obvious to some, exploring this question opens doors to understanding fundamental concepts in mathematics, particularly fractions, multiplication, and their applications in various fields. We'll move beyond the basic arithmetic to explore the conceptual underpinnings, practical examples, and even some advanced applications.
Meta Description: This comprehensive guide explores the mathematical concept of multiplying fractions, specifically focusing on "2 copies of 1/10." We delve into the basic arithmetic, practical applications, and explore related concepts to provide a thorough understanding.
Understanding Fractions: A Foundation
Before tackling the core question, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator, which indicates the number of parts we have, and the denominator, which indicates the total number of equal parts the whole is divided into. In our case, 1/10 means we have one part out of ten equal parts.
Think of a pizza cut into ten slices. 1/10 represents one slice of that pizza. Understanding this visual representation is crucial for grasping fractional concepts. Other examples include measuring ingredients in a recipe (1/10 of a cup of sugar) or calculating portions (1/10 of a budget allocated to savings).
Multiplication with Fractions: The Core Concept
The question "2 copies of 1/10 is...?" is essentially a multiplication problem: 2 x (1/10). When multiplying a whole number by a fraction, we essentially multiply the whole number by the numerator and keep the denominator the same.
Therefore:
2 x (1/10) = (2 x 1) / 10 = 2/10
This simplifies to 1/5 because both the numerator (2) and the denominator (10) are divisible by 2. So, the answer to our initial question is 1/5.
Visualizing the Multiplication: A Practical Approach
Visual aids can significantly improve understanding, particularly when working with fractions. Imagine we have two groups of objects, each containing one-tenth of a set. If we combine those two groups, we have two-tenths, which simplifies to one-fifth.
Let's take another example. Consider a meter stick divided into ten equal centimeters. 1/10 of a meter is one centimeter. Two copies of 1/10 of a meter would be two centimeters, which is 2/10 of a meter, or 1/5 of a meter. This simple example clearly demonstrates the concept.
Beyond the Basics: Extending the Concept
The fundamental concept of multiplying fractions extends far beyond this simple example. We can apply the same principle to more complex fractions and scenarios. For example:
-
Multiplying Fractions by Fractions: If we wanted to find 1/2 of 1/10, we would multiply the numerators and the denominators: (1/2) x (1/10) = 1/20.
-
Mixed Numbers: When dealing with mixed numbers (a whole number and a fraction), we first convert them to improper fractions (where the numerator is larger than the denominator) before multiplying. For instance, 1 1/2 x (1/10) would first become (3/2) x (1/10) = 3/20.
-
Real-world Applications: The principles of multiplying fractions are vital in countless real-world situations, including cooking, construction, finance, and many scientific fields. Consider calculating the amount of paint needed for a project, determining the correct dosage of medication, or splitting a bill equally among friends – these all involve fractions and their manipulation.
Applications in Different Fields
The seemingly simple concept of "2 copies of 1/10" has far-reaching applications across diverse disciplines:
1. Finance: In finance, fractions are ubiquitous. Calculating interest rates, understanding stock prices (often expressed as fractions of a dollar), and determining proportions of investments all rely on fractional calculations. Understanding how to work with fractions ensures accurate financial planning and analysis.
2. Engineering and Construction: Engineers and construction workers rely heavily on fractions and precision measurements. Calculations involving blueprints, material quantities, and structural components often require intricate fractional arithmetic. Accuracy is paramount in these fields, making a strong understanding of fractions essential.
3. Cooking and Baking: Recipes often use fractions to specify ingredient quantities. Understanding how to multiply fractions is crucial for scaling recipes up or down, ensuring the final product tastes as intended. A slight error in fractional measurement can significantly impact the outcome.
4. Science: Scientific experiments and data analysis frequently involve fractions and proportions. Measurements, dilutions, and statistical analysis often rely on precise fractional calculations. Accuracy and consistency in these calculations are vital for reliable scientific findings.
Advanced Concepts and Extensions
While we've focused on the basic arithmetic of "2 copies of 1/10," understanding this fundamental concept lays the groundwork for more complex mathematical explorations.
-
Decimals and Percentages: Fractions, decimals, and percentages are interconnected. 2/10 can be expressed as 0.2 (decimal) or 20% (percentage). Understanding the relationship between these three forms enhances flexibility in calculations.
-
Algebra: Algebraic equations often incorporate fractions. Solving for unknowns within equations involving fractions requires a solid understanding of fundamental fractional operations.
-
Calculus: Calculus, a branch of mathematics dealing with continuous change, builds upon fundamental concepts of fractions and limits. A strong foundation in fractional arithmetic is essential for mastering calculus.
Conclusion: The Importance of Mastering Fractions
The seemingly simple question, "2 copies of 1/10 is...?" highlights the significance of understanding fractions. This fundamental concept extends far beyond basic arithmetic, impacting various fields and laying the groundwork for more advanced mathematical concepts. Mastering fractions is not just about solving simple equations; it's about developing a crucial skill set applicable across diverse disciplines and essential for problem-solving in the real world. From financial planning to scientific experimentation, a solid grasp of fractional arithmetic remains a cornerstone of numeracy and critical thinking. The seemingly simple act of doubling 1/10 reveals a universe of mathematical possibilities and practical applications.
Latest Posts
Latest Posts
-
Gathering Information From Online Sources
Sep 15, 2025
-
7 Trillion 350 Million
Sep 15, 2025
-
Jan Burres Into The Wild
Sep 15, 2025
-
How Do You Spell Chicken
Sep 15, 2025
-
Non Vascular Plants Vs Vascular
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2 Copies Of 1/10 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.