2 N 3 4n 1
gasmanvison
Sep 05, 2025 · 5 min read
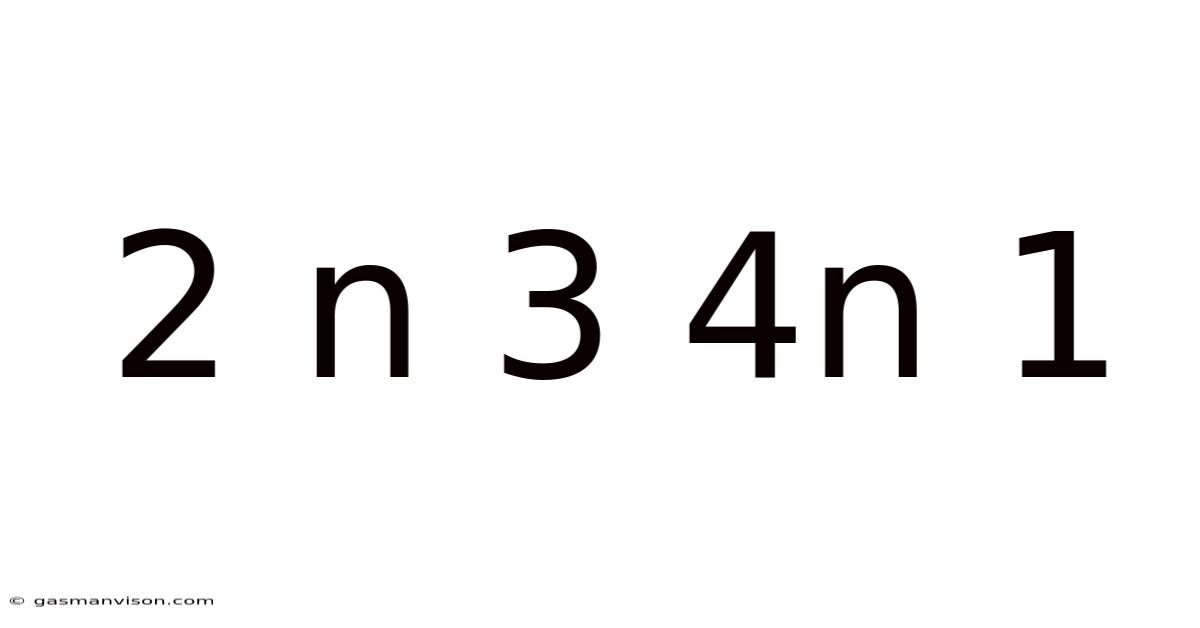
Table of Contents
Decoding the Enigma: Exploring the Mathematical Sequence 2, 3, 4n + 1
This article delves into the intriguing mathematical sequence represented by the expression "2, 3, 4n + 1," exploring its patterns, potential applications, and connections to broader mathematical concepts. While seemingly simple at first glance, this sequence opens doors to rich mathematical discussions about sequences, series, functions, and even algorithm design. This exploration will be comprehensive, aiming to provide a deep understanding suitable for both mathematical enthusiasts and those seeking to enhance their understanding of fundamental mathematical principles.
What Does 2, 3, 4n + 1 Actually Mean?
At its core, "2, 3, 4n + 1" doesn't represent a single, fixed sequence. Instead, it represents a family of sequences generated by varying the value of 'n'. The initial terms, 2 and 3, act as the starting points, while the expression '4n + 1' defines the recursive rule to generate subsequent terms. Let's break this down:
-
2 and 3: These are the first two fixed terms in every sequence generated by this rule. They are not determined by the '4n + 1' expression.
-
4n + 1: This is the recursive formula. For each successive term, we substitute a value of 'n' into this formula. The value of 'n' starts at 0 and increments by 1 for each subsequent term. This means:
- When n = 0, 4n + 1 = 1.
- When n = 1, 4n + 1 = 5.
- When n = 2, 4n + 1 = 9.
- And so on...
Therefore, depending on how many terms we want to generate, we create different sequences. For example:
- If we generate only the first three terms: The sequence would be 2, 3, 5 (where n=0 for the third term).
- If we generate five terms: The sequence becomes 2, 3, 5, 9, 13 (n=0,1,2,3 respectively for the 3rd to 5th term)
- And so on.
Exploring the Properties of the Sequence Generated by 4n+1
The sequence generated by the recursive formula 4n + 1 exhibits several interesting properties:
-
Arithmetic Progression: Notice that the sequence generated by only 4n+1 (excluding the initial 2 and 3) forms an arithmetic progression with a common difference of 4. This is a direct consequence of the linear nature of the formula. The simplicity of this progression makes it easily predictable and allows for straightforward calculation of any term within the sequence.
-
Odd Numbers: All terms generated by 4n + 1 (after the initial 2 and 3) are odd numbers. This is because 4n is always an even number, and adding 1 results in an odd number. This characteristic simplifies certain analytical processes and might have implications in number theory applications.
-
Growth Rate: The sequence demonstrates linear growth. This means the difference between consecutive terms remains constant (4), which is a key characteristic of arithmetic progressions. This predictable growth rate simplifies analysis and prediction of the sequence's behavior.
-
Relationship to other sequences: The sequence's structure allows for connections to other mathematical sequences and concepts. For instance, we can explore its relationship with Fibonacci numbers, prime numbers or even consider the sequence as a subset of a larger pattern.
Potential Applications and Connections to Other Fields
While the 2, 3, 4n + 1 sequence might seem like a purely theoretical mathematical construct, it has potential applications and connections to various fields:
-
Algorithm Design: The simple, predictable nature of the sequence could find applications in algorithm design, particularly where a linearly increasing sequence is required. This could be in areas like iteration control, data structuring, or even simple simulations.
-
Computer Science: The sequence could be used in creating simple algorithms for generating test data, or as a basis for more complex algorithms where linear growth or specific patterns are needed.
-
Cryptography (Potentially): While not immediately apparent, sequences with predictable yet complex patterns can have indirect relevance to cryptography. Understanding how sequences interact and can be manipulated could potentially inspire approaches to creating or breaking ciphers, though this is highly speculative at this stage.
Expanding the Exploration: Variations and Extensions
We can extend the exploration of this sequence by introducing variations:
-
Changing the Initial Terms: Instead of 2 and 3, we could start with different initial terms. This would alter the sequence significantly, potentially resulting in different patterns and properties. Exploring various starting points could reveal underlying mathematical relationships and symmetries.
-
Modifying the Recursive Formula: We could change the recursive formula itself. For instance, we could examine sequences generated by 3n + 1, 5n + 2, or other similar expressions. This experimentation will help to identify the effects of modifying core parameters on the overall structure and properties of the generated sequence.
-
Introducing Additional Constraints: We could add constraints, like requiring terms to be prime numbers or to satisfy certain modular arithmetic conditions. This would lead to more complex sequences with potentially interesting properties and applications, opening up avenues for deeper mathematical investigation.
-
Graphical Representation: Visualizing the sequence using graphs can offer insightful patterns and relationships that might not be immediately apparent from the numerical data alone. Different graphical representations, such as scatter plots or line graphs, could further enhance the visual analysis of this mathematical structure.
Conclusion: A Stepping Stone to Deeper Mathematical Understanding
The seemingly simple sequence 2, 3, 4n + 1 serves as an excellent example of how even seemingly basic mathematical concepts can lead to rich explorations and deeper understandings. By analyzing its properties, exploring its variations, and examining its connections to other mathematical areas, we gain valuable insights into sequences, series, functions, and their broader applications. This exploration is a stepping stone to a deeper appreciation of the elegance and interconnectedness within the field of mathematics. Further research could focus on more complex modifications of the formula, exploring its potential connections to number theory, and even investigating the potential for applying similar recursive structures to other mathematical problems. The journey of understanding this sequence, therefore, is not just about the sequence itself but also about the process of mathematical inquiry, discovery, and the joy of uncovering hidden patterns within seemingly simple systems. The possibilities for further investigation are vast and hold promise for intriguing discoveries.
Latest Posts
Latest Posts
-
Does Margarita Mix Go Bad
Sep 05, 2025
-
0 4 Repeating As A Fraction
Sep 05, 2025
-
Which Statement Must Be True
Sep 05, 2025
-
An Agents Fiduciary Responsibilities Include
Sep 05, 2025
-
Which Function Is Increasing Apex
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about 2 N 3 4n 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.