2 Square Root Of 5
gasmanvison
Sep 19, 2025 · 5 min read
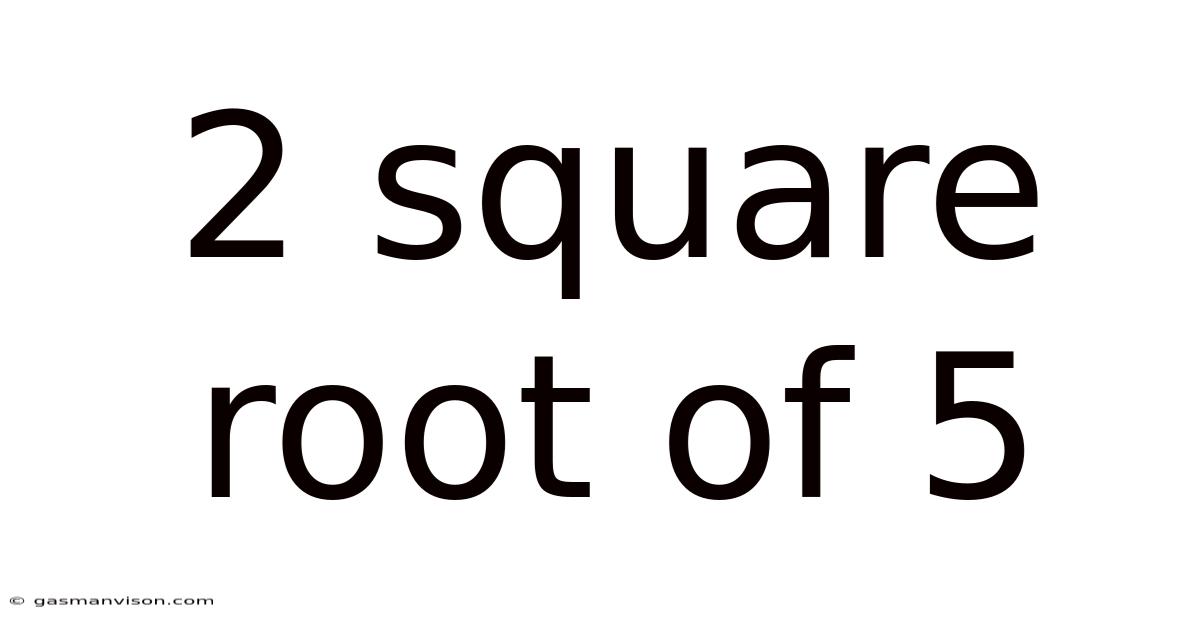
Table of Contents
Delving Deep into 2√5: Exploring its Mathematical Properties and Applications
The seemingly simple expression, 2√5, hides a wealth of mathematical richness and practical applications. This article delves deep into the exploration of this irrational number, examining its properties, calculations, and its role in various fields, from geometry and trigonometry to physics and computer science. We'll unravel its mysteries, explaining its significance and showcasing its versatility. This comprehensive guide aims to provide a clear and complete understanding of 2√5 for students, mathematicians, and anyone curious about its implications.
Understanding the Basics: What is 2√5?
At its core, 2√5 represents two times the square root of five. The square root of 5 (√5) is an irrational number, meaning it cannot be expressed as a simple fraction. Its value is approximately 2.236, resulting in 2√5 being approximately 4.472. Understanding this fundamental concept is crucial for all subsequent discussions. We'll explore how to calculate this value more precisely, and delve into its implications within broader mathematical frameworks.
Calculating 2√5: Methods and Approximations
While we know the approximate value, precisely calculating 2√5 requires understanding several mathematical approaches. The most straightforward is using a calculator, providing a high-precision decimal approximation. However, understanding the underlying mathematical principles is equally important:
-
Using a Calculator: This is the easiest method. Simply input "2 * √5" into a calculator to obtain the numerical approximation. The precision will depend on the calculator's capabilities.
-
Manual Approximation using Babylonian Method: This iterative method provides increasingly accurate approximations of square roots. Starting with an initial guess (e.g., 2), the method refines the guess using the formula:
x_(n+1) = 0.5 * (x_n + 5/x_n). Repeating this process multiple times yields a more precise approximation of √5, which can then be multiplied by 2. -
Continued Fractions: √5 can be represented as a continued fraction:
2 + 1/(4 + 1/(4 + 1/(4 + ...))). This infinite fraction provides an alternative method for approximating √5, although it's more computationally intensive than the Babylonian method.
Geometric Interpretations of 2√5
The number 2√5 appears frequently in geometric contexts, often related to the Pythagorean theorem. Consider the following examples:
-
Right-Angled Triangles: Imagine a right-angled triangle with legs of length 2 and √5. The hypotenuse, according to the Pythagorean theorem (a² + b² = c²), will have a length of √(2² + (√5)²) = √(4 + 5) = 3. Conversely, a right-angled triangle with legs of length 'a' and 'b' and a hypotenuse of length 2√5 can be analyzed using the theorem to determine the lengths of the legs, depending on the values assigned to 'a' or 'b'. Many geometric problems involve triangles that lead to calculations involving 2√5.
-
Golden Ratio Connections: Although not a direct relationship, the golden ratio (approximately 1.618) is closely related to √5 (the golden ratio is (1 + √5)/2). Geometric constructions involving the golden ratio might indirectly incorporate 2√5 in their calculations.
Trigonometric Applications of 2√5
Trigonometric functions often involve irrational numbers, and 2√5 is no exception. The exact context will depend on the specific trigonometric problem; however, various trigonometric identities and formulas might lead to expressions involving 2√5 during calculations. For example, solving for angles in certain triangles where sides are related to √5 would inevitably result in the appearance of 2√5 within the calculations, be it within sine, cosine, or tangent equations.
Applications in Physics and Engineering
In various physics and engineering applications, 2√5, or its approximation, might appear in calculations related to:
-
Vectors and Displacement: Calculations involving vectors, especially in two or three dimensions, can result in magnitudes that include 2√5. This is due to the nature of vector addition and magnitude calculations employing the Pythagorean theorem. Analyzing displacement or velocity vectors may lead to expressions involving 2√5.
-
Simple Harmonic Motion: Problems involving oscillating systems, often described by sinusoidal functions, can lead to calculations where 2√5 arises in determining amplitude, frequency, or phase constants.
-
Fluid Dynamics: Certain equations governing fluid flow, especially in contexts involving turbulence, can result in expressions containing square roots of numbers, potentially including 2√5, dependent on the specific parameters and initial conditions. These often involve complex calculations within multi-variable calculus.
2√5 in Computer Science and Algorithms
While not a direct component of many standard algorithms, 2√5's properties can be relevant in specific computational contexts:
-
Numerical Analysis: Approximations and error analysis within numerical computation might utilize methods that indirectly deal with 2√5 or its related values, as accurate representations of irrational numbers is a crucial aspect of computer-based numerical analysis.
-
Game Development and Graphics: In game development and 3D graphics rendering, the number 2√5 (or its approximation) might be used as a scaling factor or in various calculations to position objects or define shapes within a three-dimensional space, utilizing its mathematical properties to solve issues concerning vector lengths and geometrical representations. This is a hidden application where approximations of this number are utilized.
Beyond the Basics: Advanced Mathematical Explorations
The mathematical properties of 2√5 extend beyond its basic calculations and geometric interpretations:
-
Algebraic Manipulation: 2√5 can be incorporated into algebraic equations and manipulated using standard algebraic rules. Solving for unknowns in equations involving 2√5 might require advanced algebraic techniques.
-
Complex Numbers: The number 2√5 can be part of complex number calculations, where it might interact with imaginary numbers. This opens up more advanced mathematical possibilities.
-
Field Extensions: Within abstract algebra, 2√5 plays a role in field extensions where we extend the field of rational numbers (Q) by adjoining √5. Understanding these concepts requires an understanding of abstract algebra.
Conclusion: The Versatility of 2√5
This comprehensive exploration of 2√5 demonstrates that this seemingly simple mathematical expression holds significant depth and broad applicability. From its fundamental properties and calculations to its roles in geometry, trigonometry, physics, and computer science, 2√5 showcases the interconnectedness of mathematical concepts and their impact on various scientific and technological domains. Understanding this number and its properties is crucial for solving a broad spectrum of problems. While the immediate relevance might not be apparent in everyday life, its presence underscores the underlying mathematical frameworks that govern many aspects of the physical world and technological advancements.
Latest Posts
Latest Posts
-
The Iymphoid Cell Line Produces
Sep 19, 2025
-
What Is 5g Ultra Capcity
Sep 19, 2025
-
What Bonds All Marines Cohesively
Sep 19, 2025
-
Controlled Railroad Crossings Usually Have
Sep 19, 2025
-
What Colonys Founders Believed That
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.