250 Plus What Equals 1000
gasmanvison
Sep 25, 2025 · 5 min read
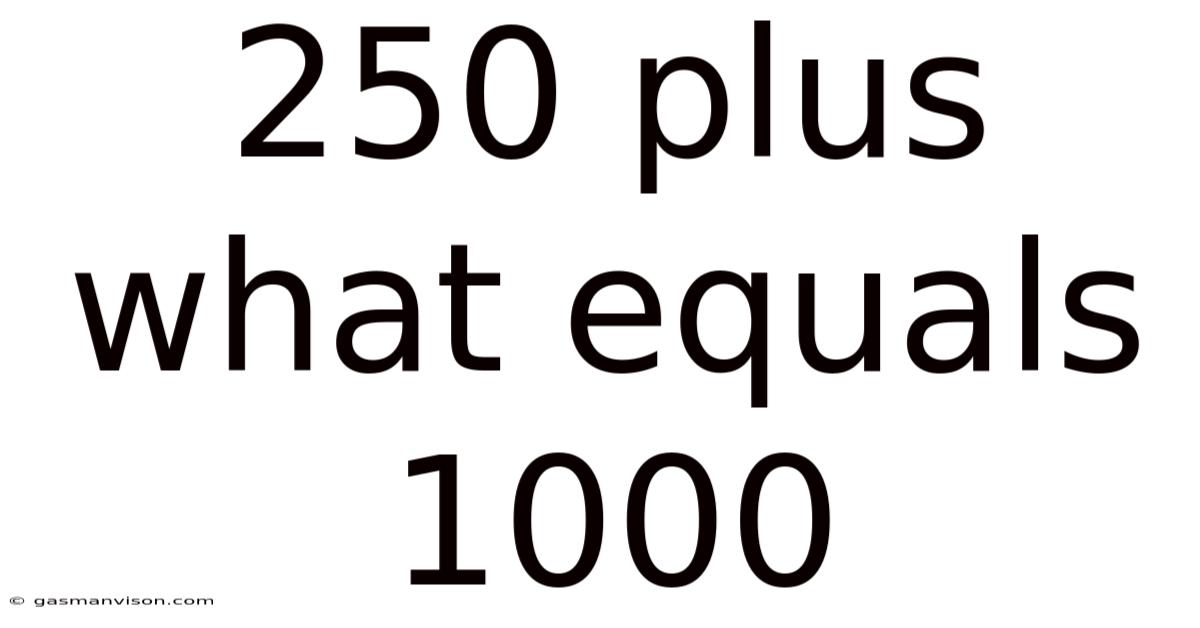
Table of Contents
250 Plus What Equals 1000: Exploring Mathematical Concepts and Problem-Solving Strategies
This article delves into the seemingly simple question: "250 plus what equals 1000?" While the answer itself is straightforward, exploring the problem allows us to unpack fundamental mathematical concepts, explore different problem-solving approaches, and highlight the importance of understanding mathematical operations in various contexts. This exploration will move beyond a simple arithmetic solution, delving into the underlying principles and demonstrating the value of mathematical reasoning.
Meta Description: Discover the solution to "250 plus what equals 1000" and explore the underlying mathematical concepts. This article provides multiple approaches to problem-solving, highlighting the importance of mathematical reasoning and its applications. Learn about inverse operations, algebraic equations, and practical applications of this simple equation.
Understanding the Problem: A Foundation in Arithmetic
At its core, the question "250 plus what equals 1000" presents a simple addition problem. We are seeking an unknown value (let's call it 'x') that, when added to 250, results in a sum of 1000. This can be represented mathematically as:
250 + x = 1000
This equation forms the basis of our exploration. Understanding this basic algebraic representation is crucial, as it lays the groundwork for more complex mathematical problems. The equation highlights the relationship between the known values (250 and 1000) and the unknown value (x), which we aim to find.
Solving the Equation: Applying Inverse Operations
The most direct method to solve this equation is to utilize inverse operations. Addition and subtraction are inverse operations; they "undo" each other. To isolate 'x' and find its value, we perform the inverse operation of addition, which is subtraction. We subtract 250 from both sides of the equation:
250 + x - 250 = 1000 - 250
This simplifies to:
x = 750
Therefore, 250 plus 750 equals 1000. This is the direct and most efficient solution to the problem. The application of inverse operations is a fundamental skill in algebra and is applicable to a wide range of mathematical problems.
Alternative Approaches: Different Perspectives on Problem-Solving
While the inverse operation method is efficient, exploring alternative approaches can enhance our understanding and demonstrate the flexibility of mathematical thinking.
-
Subtraction as a Primary Operation: Instead of viewing the problem as "250 plus what equals 1000," we can frame it as "1000 minus 250 equals what?" This directly leads to the subtraction operation: 1000 - 250 = 750. This approach emphasizes the relationship between addition and subtraction and highlights the interchangeable nature of these operations in solving certain problems.
-
Mental Math Techniques: For simple equations like this, mental math techniques can be employed. We can break down the problem into smaller, more manageable parts. For example, we could subtract 200 from 1000, resulting in 800, and then subtract the remaining 50, yielding 750. This method highlights the importance of number sense and mental agility in problem-solving.
-
Visual Representation: A visual representation, such as a number line, can be helpful, especially for those who prefer a more concrete approach. Starting at 250 on the number line, we can count or visually determine the distance needed to reach 1000. This method can be particularly useful for younger learners or those who are visually oriented.
-
Using a Calculator: While less intellectually stimulating, using a calculator can be a practical approach, especially when dealing with larger or more complex numbers where mental calculation might be time-consuming or prone to error. The calculator verifies the solution obtained through other methods, providing confirmation of accuracy.
Extending the Problem: Real-World Applications and Problem-Solving Strategies
The simple equation "250 + x = 1000" transcends its apparent simplicity and finds applications in various real-world scenarios. Consider these examples:
-
Budgeting: If you have $250 saved and need $1000 for a purchase, you need to determine how much more money you need to save (x = $750).
-
Inventory Management: If you have 250 units of a product in stock and need 1000 units to meet demand, you need to order an additional 750 units.
-
Project Planning: If you've completed 250 tasks out of a total of 1000, you have 750 tasks remaining.
These examples demonstrate the practical relevance of this seemingly basic mathematical problem. The ability to solve such equations is a fundamental skill for effective problem-solving in various real-world contexts.
Exploring Related Concepts: Expanding Mathematical Understanding
Beyond the immediate solution, exploring related mathematical concepts enriches our understanding.
-
Algebraic Equations: The equation 250 + x = 1000 is a simple algebraic equation. Understanding how to solve algebraic equations is fundamental to more advanced mathematics. The principles of inverse operations and isolating variables are crucial skills in algebra.
-
Percentage Calculations: We can frame the problem in terms of percentages. 250 is 25% of 1000 (250/1000 * 100 = 25%). Therefore, the remaining 75% (750) represents the amount needed to reach 1000.
-
Proportions and Ratios: The relationship between 250 and 1000 can be expressed as a ratio: 250:1000, which simplifies to 1:4. This highlights the proportional relationship between the two numbers.
-
Number Systems: The problem can be solved using different number systems (binary, hexadecimal, etc.), expanding our understanding of number representation and mathematical operations in diverse contexts.
Conclusion: The Significance of Simple Problems
The seemingly simple question, "250 plus what equals 1000," offers a rich opportunity to explore fundamental mathematical concepts, practice problem-solving strategies, and understand the real-world applications of mathematics. From inverse operations and algebraic equations to mental math techniques and visual representations, various approaches highlight the flexibility and power of mathematical reasoning. The ability to solve such problems is not only a fundamental mathematical skill but also a valuable tool for tackling more complex challenges in various fields. The exploration of this simple equation underscores the importance of a solid mathematical foundation and the diverse ways in which we can approach and solve mathematical problems. Understanding these principles lays the groundwork for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
Burger And Grape Snow Cone
Sep 25, 2025
-
8 4k 4 5k 32
Sep 25, 2025
-
9 Times What Equals 81
Sep 25, 2025
-
How Many Oz 1 Pound
Sep 25, 2025
-
How Big Is 2 M
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 250 Plus What Equals 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.