3 1/8 In Decimal Form
gasmanvison
Sep 20, 2025 · 5 min read
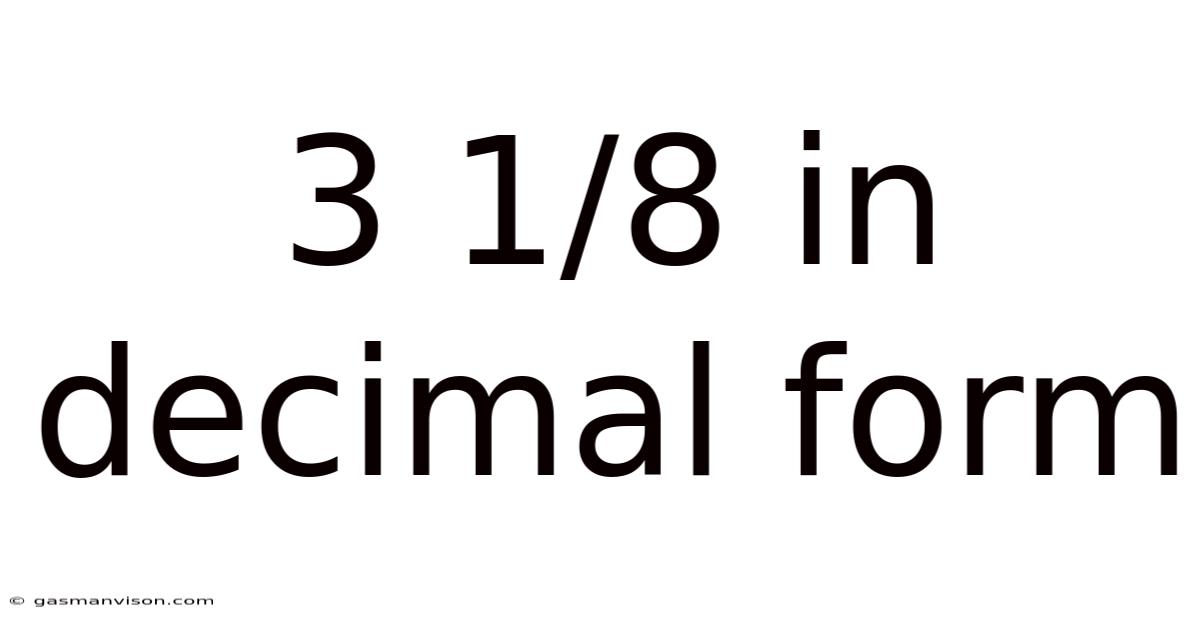
Table of Contents
Decoding 3 1/8: A Deep Dive into Decimal Conversion and Practical Applications
This article will explore the conversion of the mixed number 3 1/8 into its decimal equivalent, offering a detailed explanation of the process and highlighting its practical applications across various fields. Understanding this seemingly simple conversion unlocks a deeper appreciation of fractional arithmetic and its relevance in real-world scenarios. We'll delve into the method itself, explore alternative approaches, and discuss where this knowledge proves invaluable.
What is 3 1/8? Understanding Mixed Numbers and Fractions
Before diving into the conversion, let's establish a firm understanding of what 3 1/8 represents. This is a mixed number, combining a whole number (3) and a proper fraction (1/8). The mixed number signifies a quantity greater than three but less than four, representing three whole units and one-eighth of another unit. This fractional component, 1/8, signifies one part out of a total of eight equal parts. Understanding this fundamental concept is crucial for accurate conversion.
Converting 3 1/8 to Decimal Form: The Step-by-Step Guide
There are several methods to convert 3 1/8 into its decimal equivalent. We'll outline the most common and straightforward approach:
-
Convert the fraction to an improper fraction: To work efficiently with the fraction, we first transform the mixed number into an improper fraction. We do this by multiplying the whole number (3) by the denominator of the fraction (8), adding the numerator (1), and keeping the same denominator. This gives us: (3 * 8) + 1 = 25. Therefore, 3 1/8 becomes 25/8.
-
Divide the numerator by the denominator: Now we perform the division: 25 ÷ 8. This division can be carried out using long division, a calculator, or even mental arithmetic if you're comfortable with it.
-
Obtain the decimal result: Performing the division 25 ÷ 8 yields 3.125.
Therefore, 3 1/8 in decimal form is 3.125.
Alternative Methods for Conversion
While the above method is the most common and straightforward, other approaches can be used, particularly beneficial for understanding the underlying principles:
-
Using Decimal Equivalents of Common Fractions: Knowing that 1/8 is equal to 0.125, we can simply add this to the whole number 3: 3 + 0.125 = 3.125. This method highlights the importance of memorizing common fraction-to-decimal conversions.
-
Long Division: Long division provides a detailed understanding of the division process. Writing out the steps helps solidify the concept and is particularly useful for those who are less familiar with decimal conversions. While potentially more time-consuming, it provides a valuable learning opportunity.
-
Calculator Use: Calculators provide a quick and efficient way to convert fractions to decimals. Simply enter 25/8 and the calculator will display the decimal equivalent, 3.125. This method is ideal for speed and accuracy, especially when dealing with more complex fractions.
Practical Applications of 3.125 and Decimal Conversions
The ability to convert fractions to decimals is essential across various disciplines:
-
Engineering and Construction: In engineering and construction, precise measurements are critical. Converting fractions to decimals allows for accurate calculations and ensures the seamless integration of different measurements in blueprints and designs. Imagine calculating the dimensions of a building component where fractions are specified – the decimal equivalent facilitates easy calculations.
-
Manufacturing and Machining: In manufacturing and machining, precision is paramount. Decimal representation of measurements ensures accuracy in creating parts and components. For instance, setting a machine to a specific dimension requires decimal precision.
-
Finance and Accounting: Decimal conversions are fundamental in finance and accounting. Calculations involving interest rates, currency exchange, and stock prices often require working with decimals. Understanding fraction-to-decimal conversion ensures accurate financial computations.
-
Cooking and Baking: In cooking and baking, precise measurements are vital for achieving the desired outcome. Converting fractional measurements from recipes into their decimal equivalents can lead to more precise results.
-
Scientific Calculations: Science and research often involve measurements and calculations that require fractions to be expressed as decimals. This is important for data analysis and interpretation.
-
Data Analysis and Statistics: When working with data sets, converting fractions to decimals makes statistical calculations and data analysis simpler. Many statistical software packages operate exclusively using decimals.
-
Computer Programming: In computer programming, decimal representation is crucial for numerical computations. Many programming languages use floating-point numbers (decimals) to represent fractions.
-
Everyday Life: While not always explicitly recognized, decimal conversions are used in various everyday scenarios. From calculating fuel efficiency to dividing up costs amongst friends, understanding decimal representations simplifies many daily calculations.
Beyond 3 1/8: Mastering Decimal Conversions
The process of converting 3 1/8 to its decimal form serves as a foundation for understanding decimal conversions more broadly. The same principles apply to converting any fraction, whether it's a proper fraction, an improper fraction, or part of a mixed number. Mastering this fundamental skill opens doors to more complex calculations and problem-solving across various fields.
Conclusion: The Importance of Fractional and Decimal Fluency
Understanding the conversion of fractions to decimals, illustrated clearly through the example of 3 1/8, is a vital skill. This knowledge empowers you to approach various mathematical, scientific, and practical problems with greater efficiency and accuracy. Whether you are an engineer, accountant, baker, or simply someone navigating everyday life, mastering this fundamental concept will enhance your problem-solving capabilities and overall numerical literacy. The ability to seamlessly move between fractional and decimal representations is a crucial element of numerical proficiency, offering a significant advantage in a wide range of contexts. The seemingly simple conversion of 3 1/8 to 3.125 unveils a world of practical applications and underscores the interconnectedness of different mathematical representations.
Latest Posts
Latest Posts
-
What Should A Conclusion Include
Sep 20, 2025
-
Half Of 1 1 2 Teaspoons
Sep 20, 2025
-
Mai Biked 6 3 4
Sep 20, 2025
-
Tesla Is Using Accrual Accounting
Sep 20, 2025
-
Pickering V Board Of Ed
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 1/8 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.