3.26d + 9.75d - 2.65
gasmanvison
Sep 06, 2025 · 5 min read
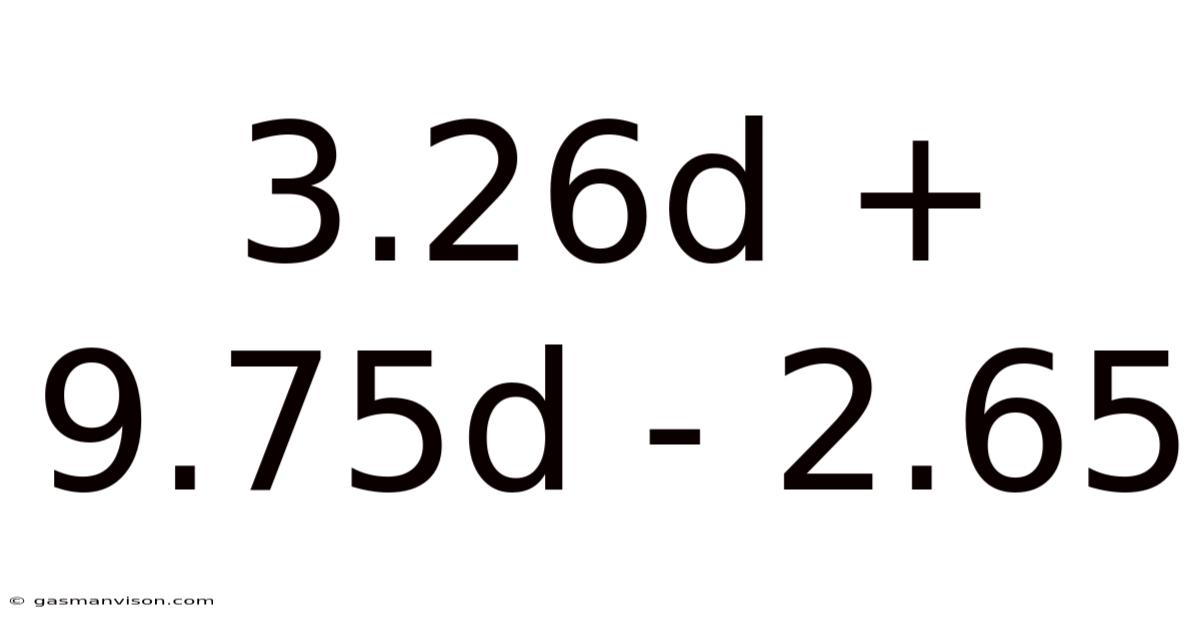
Table of Contents
Deconstructing 3.26d + 9.75d - 2.65: A Deep Dive into Algebraic Simplification and its Applications
This article will delve into the seemingly simple algebraic expression 3.26d + 9.75d - 2.65, exploring its simplification, practical applications, and the broader mathematical concepts it embodies. While the expression itself might appear straightforward, understanding its nuances reveals fundamental principles crucial for anyone navigating algebra and beyond. We'll unpack the process of simplification, discuss the role of variables, and examine how this type of expression finds its way into various real-world scenarios.
Understanding the Expression: Variables and Constants
Before jumping into the simplification, let's define the components of the expression: 3.26d + 9.75d - 2.65. This expression is a linear algebraic equation, meaning it involves only terms with variables raised to the power of one (or zero, in the case of constants).
-
Variables: The 'd' in the expression represents a variable. A variable is an unknown quantity or a placeholder for a value that can change. In this case, 'd' could represent any number – distance, density, dollars, or any other quantity you choose.
-
Coefficients: The numbers 3.26 and 9.75 are coefficients. Coefficients are the numerical multipliers of the variables. They tell us how many 'd's we have in each term.
-
Constants: The number -2.65 is a constant. Constants are numerical values that do not change; they are independent of the variable 'd'.
Simplifying the Expression: Combining Like Terms
The core of solving this expression lies in combining like terms. Like terms are terms that contain the same variables raised to the same power. In our expression, 3.26d and 9.75d are like terms because they both contain the variable 'd' raised to the power of 1.
To simplify, we add the coefficients of the like terms:
3.26d + 9.75d = (3.26 + 9.75)d = 13.01d
Therefore, the simplified expression becomes:
13.01d - 2.65
This is the simplest form of the original expression. We cannot further simplify it because 13.01d and -2.65 are unlike terms (one contains the variable 'd', the other is a constant).
Solving for 'd': Finding the Value of the Variable
The simplified expression, 13.01d - 2.65, represents a linear equation. To solve for 'd', we need more information. We need to know the value of the entire expression or have it set equal to another value.
For instance, if the expression is equal to 0, we have:
13.01d - 2.65 = 0
We can then solve for 'd':
13.01d = 2.65 d = 2.65 / 13.01 d ≈ 0.2037
This means that if the entire expression is equal to zero, the value of 'd' is approximately 0.2037.
Similarly, if the expression is equal to a different value, say 10, we would have:
13.01d - 2.65 = 10 13.01d = 12.65 d = 12.65 / 13.01 d ≈ 0.9723
The value of 'd' depends entirely on the value the entire expression is equal to.
Real-World Applications: Where This Expression Might Appear
Although seemingly abstract, expressions like 3.26d + 9.75d - 2.65 frequently appear in various real-world applications:
1. Calculating Costs and Profits:
Imagine a scenario involving the manufacturing and sale of a product. Let's say 'd' represents the number of units produced.
- 3.26d could represent the direct material cost per unit.
- 9.75d could represent the labor cost per unit.
- 2.65 could represent a fixed overhead cost (like rent or utilities), regardless of the number of units produced.
The entire expression, 3.26d + 9.75d - 2.65, would then represent the total profit (or loss) based on the number of units produced and sold, assuming a fixed selling price. By substituting different values of 'd', we can analyze profit margins at different production levels. Analyzing this allows businesses to determine optimal production levels for maximum profitability or break-even points.
2. Calculating Distance and Speed:
Let's say 'd' represents distance. We could have different segments of a journey.
- 3.26d might be the distance covered at a certain speed in one segment.
- 9.75d might represent the distance covered at a different speed in another segment.
- -2.65 might represent a reduction in distance due to a detour or a mistake in navigation.
The entire expression would represent the total net distance covered after accounting for all the segments and adjustments. This is useful in logistics, travel planning, and even in GPS navigation systems that constantly recalculate routes.
3. Financial Modeling and Investments:
In finance, 'd' could represent the number of shares of a particular stock.
- 3.26d could represent the initial investment.
- 9.75d could represent the gains from the investment.
- -2.65 could represent brokerage fees or taxes.
This expression would then calculate the net return on the investment. By altering the value of 'd' and considering other financial metrics, complex financial models can be created to analyze investment strategies and forecast future performance.
4. Physics and Engineering:
In physics and engineering, 'd' could represent various physical quantities like displacement, density, or even time. This type of equation could be part of a larger system of equations used to model various physical phenomena.
5. Scientific Research and Data Analysis:
Researchers often use similar algebraic expressions to model relationships between variables in experiments. They can substitute data points to test hypotheses and understand patterns in collected data.
Expanding on the Concepts: Beyond Simple Simplification
While this article focuses on a simple algebraic expression, the underlying principles extend to more complex mathematical concepts. Understanding the simplification of like terms is fundamental to:
-
Solving systems of equations: More complex problems often involve multiple variables and equations. The ability to simplify expressions is crucial for solving these systems.
-
Calculus: Calculus builds upon the foundations of algebra, using similar simplification techniques to solve problems involving rates of change and areas under curves.
-
Linear algebra: This branch of mathematics deals with vectors and matrices, and the simplification of expressions is crucial for manipulating and solving linear equations in higher dimensions.
Conclusion: The Power of Simplicity
The seemingly simple expression 3.26d + 9.75d - 2.65 reveals the power and utility of basic algebraic manipulation. By understanding the concepts of variables, constants, coefficients, and like terms, we can simplify this expression and apply it to a wide range of real-world situations. This understanding forms a cornerstone of more advanced mathematical concepts and is essential for solving complex problems in numerous fields. The ability to simplify and manipulate algebraic expressions is not just a mathematical skill; it's a crucial problem-solving tool with far-reaching applications.
Latest Posts
Latest Posts
-
What Is Verbal Security Blanket
Sep 06, 2025
-
Provide For Common Defense Definition
Sep 06, 2025
-
Porous Water Absorbing Mass Of Fibers
Sep 06, 2025
-
Fcc A And R Relationship
Sep 06, 2025
-
18 Degrees Celsius To F
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 3.26d + 9.75d - 2.65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.