3 4 3 4 Equals
gasmanvison
Sep 17, 2025 · 5 min read
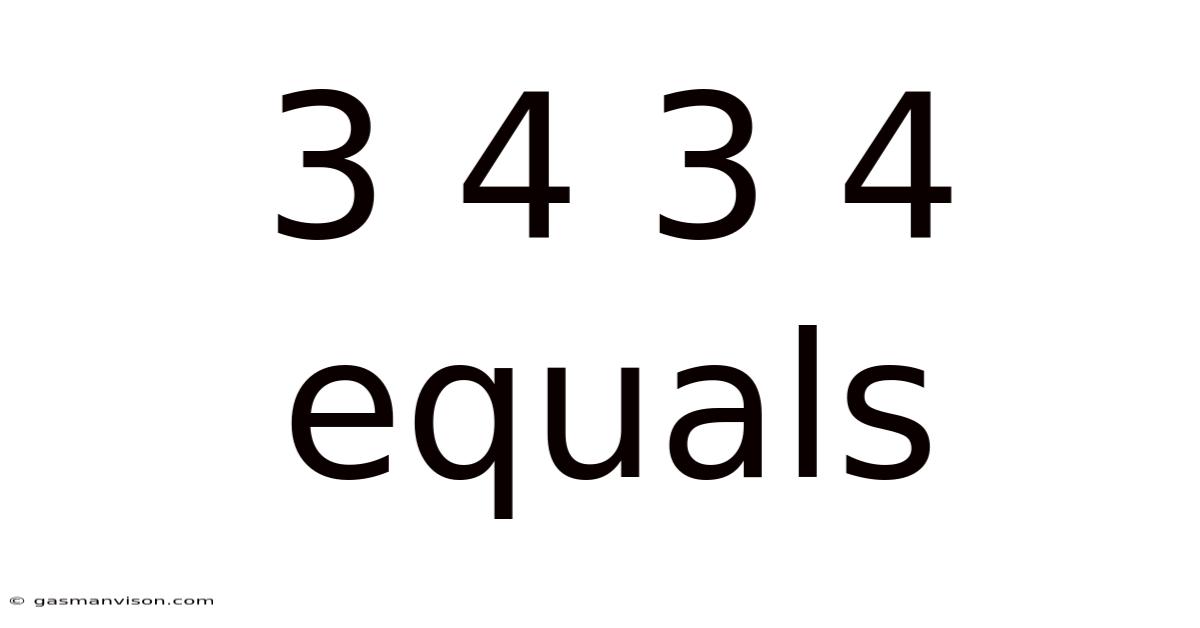
Table of Contents
3 4 3 4 Equals: Unlocking the Mystery of Mathematical Puzzles and Problem-Solving Strategies
This seemingly simple equation, "3 4 3 4 equals," is not a straightforward mathematical problem. Instead, it's a puzzle that requires creative thinking and a departure from traditional arithmetic operations. This article delves into the intriguing world of mathematical puzzles, exploring various problem-solving techniques and potential solutions to the "3 4 3 4 equals" enigma. We'll unravel the logic behind such puzzles, discuss the importance of pattern recognition, and consider how lateral thinking can unlock seemingly impossible problems. The ultimate goal is to demonstrate how approaching such puzzles can enhance your analytical skills and critical thinking abilities, applicable far beyond the realm of mathematics.
What Makes This Puzzle Unique?
The puzzle's deceptiveness lies in its apparent simplicity. We're conditioned to solve mathematical equations using standard arithmetic – addition, subtraction, multiplication, and division. However, "3 4 3 4 equals" defies this approach. There's no single, universally accepted "correct" answer. The beauty of this type of puzzle lies in the multitude of potential solutions, each requiring a different approach and demonstrating unique problem-solving strategies. The answer, therefore, isn't about finding the answer but rather exploring possible answers and understanding the underlying logic. This is a crucial difference compared to standard mathematical problems, moving from calculation to interpretation and lateral thinking.
Problem-Solving Strategies: Beyond the Obvious
To tackle this puzzle, we need to move beyond the confines of basic arithmetic. Several approaches can be employed, and understanding them illuminates the diverse techniques applicable to a wider range of problem-solving scenarios:
1. Exploring Different Number Systems:
-
Binary Code: Could the numbers represent binary digits? While unlikely to directly yield a simple solution to "3 4 3 4 equals," exploring alternative number systems expands our understanding of numerical representation and opens doors to creative solutions in similar puzzles. A deeper dive into binary, octal, or hexadecimal systems could reveal unexpected connections or interpretations.
-
Roman Numerals: Representing the numbers as Roman numerals (III, IV, III, IV) doesn't directly provide an answer, but it illustrates the idea of exploring different numerical notations. This expands our thinking beyond the base-10 system we typically use.
2. Incorporating Mathematical Operations and Symbols:
-
Concatenation: Instead of performing operations between the numbers, we could consider combining them. Concatenating the numbers (3434) could be a starting point for further mathematical manipulations. We could then explore various arithmetic operations on this larger number.
-
Exponents and Roots: Introducing exponents or roots opens up a world of possibilities. For instance, could 3⁴ + 3⁴ equal a specific value? Experimenting with different mathematical functions broadens the solution space significantly.
-
Factorials and other Advanced Functions: Factorials (!), logarithms, and other advanced mathematical functions significantly extend the potential solution paths. While complex, exploring these options demonstrates a proactive and rigorous approach to problem-solving.
3. The Role of Geometry and Visual Representation:
-
Spatial Reasoning: Could the numbers represent dimensions or coordinates in a geometric problem? The puzzle could be hinting at a spatial relationship, not directly a numerical equation.
-
Visual Analogies: Imagine representing the numbers visually. Could a pattern emerge from a graphic representation that unlocks the solution? This approach emphasizes the power of visualization in problem-solving.
4. Lateral Thinking and Creative Interpretations:
The "3 4 3 4 equals" puzzle particularly encourages lateral thinking. Consider these creative approaches:
-
Wordplay: Could "3 4 3 4" represent something entirely different when interpreted as words or symbols? This opens the door to creative interpretations and necessitates thinking beyond pure mathematics. This technique often involves clever re-interpretation of the problem statement.
-
Hidden Patterns: Is there a hidden pattern in the sequence "3 4 3 4"? Looking for repeating patterns or relationships between the numbers is crucial. This strategy relies on pattern recognition skills often applied in many areas beyond mathematics.
-
Contextual Clues: While there are no explicitly stated clues, the very nature of presenting this as a puzzle implies some level of unconventional solution. This suggests the answer might not be readily apparent through traditional mathematical methods.
Examples of Possible Solutions (Illustrative, not definitive):
Let's illustrate a few possible solutions, emphasizing the process rather than claiming a single "correct" answer:
-
Concatenation and Subtraction: If we concatenate 3434, we get 3434. We could then subtract a number to reach a target value. For example, 3434 - 3400 = 34. This shows how combining numbers and applying arithmetic can lead to solutions.
-
Exponents and Addition: 3⁴ + 3⁴ = 81 + 81 = 162. This is one possible numerical result if we utilize exponents.
-
Base Conversion and Arithmetic: Consider converting 3 and 4 to another base system, performing an operation, and then converting back. The complexity of this approach demonstrates the depth of possibilities.
The Importance of Problem-Solving Techniques in Everyday Life:
The seemingly simple puzzle "3 4 3 4 equals" highlights the significance of diverse problem-solving approaches in various aspects of life. The skills honed while tackling such puzzles are transferable:
-
Enhanced Analytical Skills: The process encourages critical thinking and breaking down complex problems into manageable parts.
-
Improved Lateral Thinking: The puzzle encourages thinking outside the box and exploring unconventional solutions.
-
Strengthened Pattern Recognition: Identifying patterns and relationships is crucial for problem-solving in many fields.
-
Increased Creativity: The open-ended nature of the puzzle fosters creative thinking and innovative approaches.
Conclusion: Embracing the Ambiguity
The "3 4 3 4 equals" puzzle is not about finding the answer but about the process of exploring potential solutions. It's a testament to the richness and diversity of problem-solving strategies. By embracing the ambiguity and exploring different approaches, we hone essential skills applicable far beyond the realm of mathematical puzzles. The puzzle serves as a powerful tool for improving critical thinking, analytical abilities, and creative problem-solving – skills vital in navigating the complexities of life and work. It encourages perseverance and the realization that sometimes, the most satisfying solutions are found not in the destination, but in the journey of exploration itself. The true value lies in the experience of engaging with the problem and applying a variety of problem-solving methodologies.
Latest Posts
Latest Posts
-
What Is 120 Of 20
Sep 17, 2025
-
Evaluate Log1255 Mc001 1 Jpg Mc001 2 Jpg Mc001 3 Jpg
Sep 17, 2025
-
Advantages And Disadvantages Of Hcs
Sep 17, 2025
-
2 Lbs To Cups Conversion
Sep 17, 2025
-
1 7 8 In Decimal
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 4 3 4 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.