3 4 Divided By 3
gasmanvison
Sep 16, 2025 · 5 min read
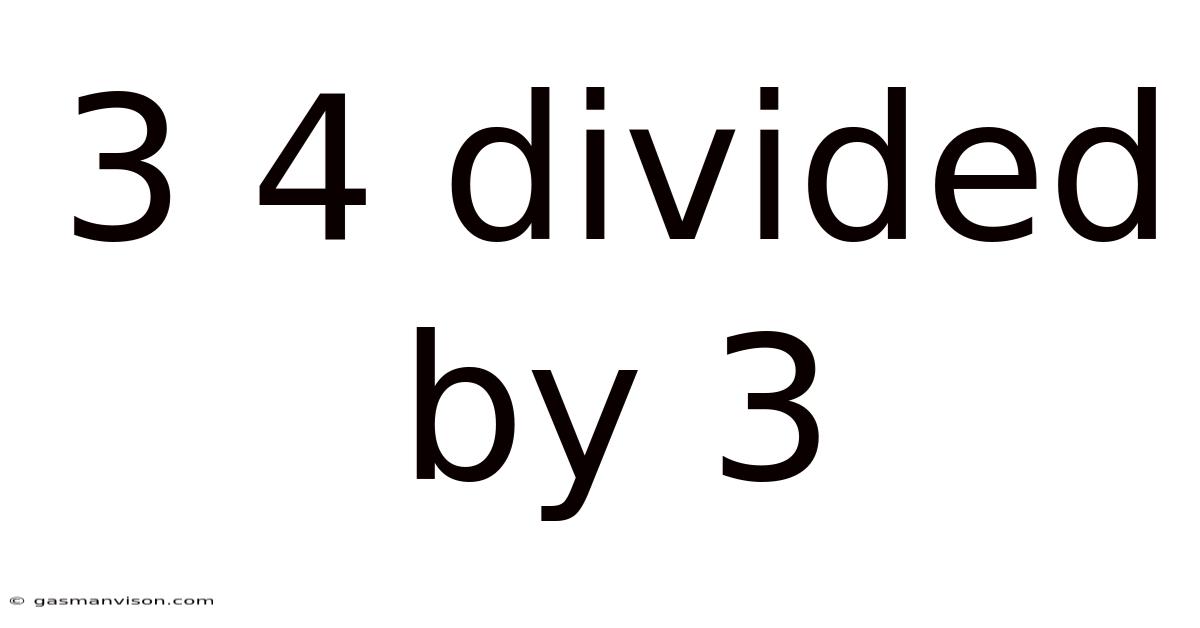
Table of Contents
Decoding 3/4 Divided by 3: A Deep Dive into Fraction Division
This article explores the seemingly simple yet conceptually rich problem of dividing the fraction 3/4 by 3. While the solution might appear straightforward at first glance, understanding the underlying principles reveals important insights into fraction manipulation and lays a solid foundation for tackling more complex mathematical problems. This guide will not only provide the solution but also break down the process step-by-step, clarifying the logic and offering alternative approaches. We'll delve into the why and how, ensuring a complete understanding of fraction division.
What is 3/4 Divided by 3? The Quick Answer
Before we embark on a detailed explanation, let's address the core question: 3/4 divided by 3 equals 1/4.
This seemingly simple answer hides a wealth of mathematical principles that are crucial for mastering fractions. The following sections will unpack the process, providing different methods to reach the same result and enhancing your understanding of fraction division.
Understanding Fraction Division: The Conceptual Basis
Division, in its essence, involves splitting a quantity into equal parts. When dealing with fractions, this concept remains the same, but the process requires a slightly different approach compared to dividing whole numbers. Think of dividing 3/4 by 3 as splitting a quantity represented by 3/4 into three equal parts. Each of these parts represents the result of the division.
Method 1: Reciprocal Multiplication
This is the most common and arguably the most efficient method for dividing fractions. The rule states that dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction inverted; the numerator becomes the denominator, and the denominator becomes the numerator.
Here's how it works for 3/4 divided by 3:
-
Rewrite the whole number as a fraction: The whole number 3 can be written as 3/1.
-
Invert the divisor (the fraction you're dividing by): The reciprocal of 3/1 is 1/3.
-
Change the division to multiplication: The problem now becomes (3/4) * (1/3).
-
Multiply the numerators and the denominators: (3 * 1) / (4 * 3) = 3/12.
-
Simplify the fraction: 3/12 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 3. This simplifies to 1/4.
Therefore, 3/4 divided by 3 = 1/4.
Method 2: Visual Representation using Models
A visual approach can enhance understanding, particularly for beginners. Imagine a rectangular shape representing the whole (1). Divide this rectangle into four equal parts, and shade three of them to represent 3/4. Now, divide these shaded three parts into three equal groups. You will find that each group represents one-fourth (1/4) of the original rectangle. This visual representation perfectly illustrates the result of the division.
Method 3: Repeated Subtraction
While less efficient for this particular problem, understanding repeated subtraction can solidify the concept of division. Division can be viewed as repeatedly subtracting the divisor until you reach zero. In this case, we would subtract 1/3 from 3/4 repeatedly. However, this method requires finding a common denominator, which might involve more complex fraction calculations. Let's illustrate this:
To subtract fractions, we need a common denominator. The least common denominator for 3/4 and 1/3 is 12. Therefore, we rewrite the fractions as:
- 3/4 = 9/12
- 1/3 = 4/12
Now we can repeatedly subtract 4/12 from 9/12:
9/12 - 4/12 = 5/12 5/12 - 4/12 = 1/12
Notice that we can only subtract 4/12 twice from 9/12. This is where the fractional part of repeated subtraction makes the process less efficient than reciprocal multiplication. The result is 1/12 remaining which, in this context, is not easily interpretable. This method's complexity is better suited to illustrating division conceptually rather than serving as a practical calculation method for this specific problem.
Real-World Applications of Fraction Division
The concept of dividing fractions, and the specific example of 3/4 divided by 3, is surprisingly relevant in various real-world situations:
-
Baking and Cooking: If a recipe calls for 3/4 cup of flour and you want to make only one-third of the recipe, you would need to calculate 3/4 divided by 3 to determine the required amount of flour.
-
Resource Allocation: Imagine you have 3/4 of a tank of gas and need to split it equally among three vehicles. The result of the division tells you how much gas each vehicle will receive.
-
Construction and Measurement: Dividing fractional measurements (e.g., dividing a 3/4-inch piece of wood into three equal sections) often occurs in construction and engineering.
-
Data Analysis: In situations where you're analyzing data represented in fractions, dividing fractions is crucial for various statistical computations.
Expanding the Concept: Dividing Fractions by Fractions
While this article focuses on dividing a fraction by a whole number, the principles extend to dividing fractions by other fractions. The reciprocal multiplication method remains the most effective technique:
For example, if you need to calculate 3/4 divided by 2/5:
-
Invert the second fraction (2/5 becomes 5/2).
-
Change the division to multiplication: (3/4) * (5/2).
-
Multiply numerators and denominators: (3 * 5) / (4 * 2) = 15/8.
This result is an improper fraction (numerator greater than denominator) which can be converted to a mixed number (1 and 7/8).
Conclusion: Mastering Fraction Division
Dividing fractions, even seemingly simple problems like 3/4 divided by 3, unveils fundamental principles crucial for mathematical fluency. Understanding the concept of reciprocals and applying the correct methods allows for efficient and accurate calculations. Whether you employ reciprocal multiplication, visual models, or (less efficiently) repeated subtraction, the goal is to grasp the underlying logic. This comprehensive understanding extends to more complex scenarios involving fraction division, providing a robust foundation for tackling future mathematical challenges. Remember, practice is key to mastering this essential skill. Try working through similar problems to build your confidence and understanding.
Latest Posts
Latest Posts
-
A Ground Fault Occurs When
Sep 16, 2025
-
How Many Inches Is 34mm
Sep 16, 2025
-
Convert 48 Inches To Feet
Sep 16, 2025
-
Which Quadrilateral Is A Kite
Sep 16, 2025
-
Button With Triangle Above Rectangle
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.