3.5 Percent As A Decimal
gasmanvison
Sep 06, 2025 · 6 min read
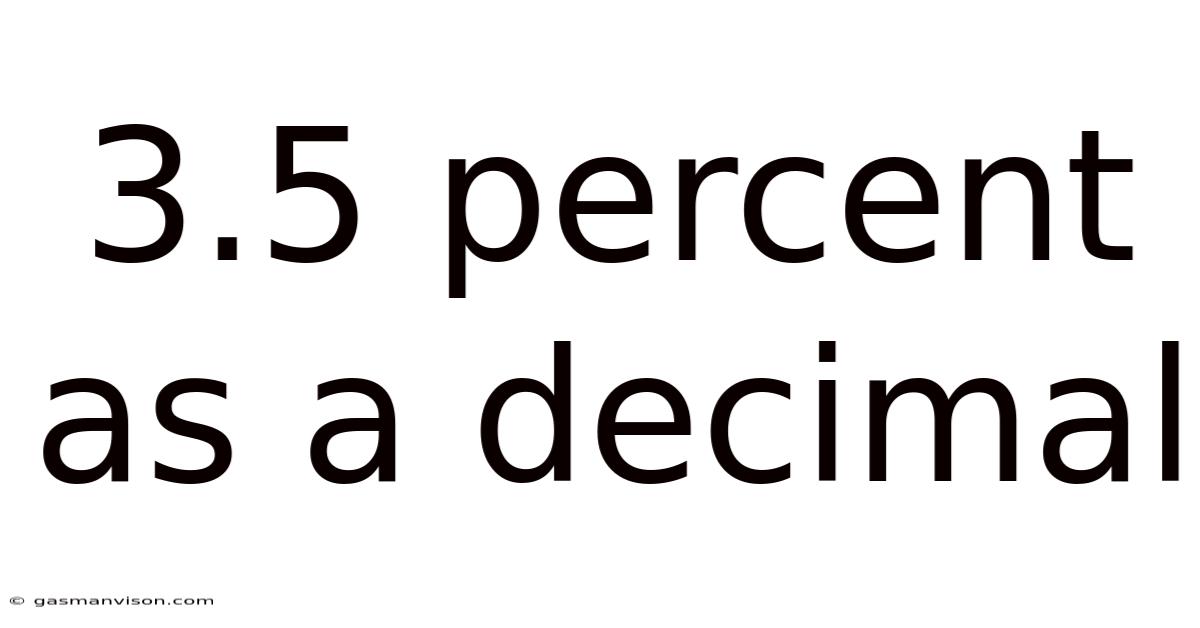
Table of Contents
3.5 Percent as a Decimal: A Comprehensive Guide
Meta Description: Understanding how to convert percentages to decimals is crucial for various applications. This comprehensive guide explains how to convert 3.5 percent to a decimal, explores the underlying principles, and provides practical examples to solidify your understanding. Learn about the importance of percentage-to-decimal conversions in math, finance, and everyday life.
Percentages are a common way to express fractions or proportions. They represent a part of a whole, where the whole is always considered 100%. However, for many mathematical calculations and especially in computer programming or spreadsheet applications, it's essential to work with decimals instead of percentages. This article will delve into the conversion of 3.5 percent to its decimal equivalent, providing a thorough explanation of the process and exploring its applications in various fields.
We'll not only show you how to convert 3.5% to a decimal but also equip you with the knowledge to confidently convert any percentage to its decimal form. This understanding is fundamental to various mathematical operations, making it a vital skill for students, professionals, and anyone dealing with numerical data.
Understanding Percentages and Decimals
Before jumping into the conversion of 3.5%, let's establish a solid understanding of the relationship between percentages and decimals. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". A decimal, on the other hand, is a way of representing a number using a base-ten system, where the digits to the right of the decimal point represent fractions of powers of ten.
The connection between the two lies in the fact that a percentage can be easily converted into a decimal by dividing the percentage value by 100. This fundamental principle applies to all percentage-to-decimal conversions, regardless of the specific percentage value.
Converting 3.5 Percent to a Decimal
The conversion of 3.5% to a decimal is a straightforward process following the principle mentioned above. Here's how it's done:
-
Remove the Percentage Sign: The first step is to remove the percentage sign (%) from the number. This leaves us with the value 3.5.
-
Divide by 100: The next step, and the core of the conversion, is to divide the number (3.5) by 100. This can be done using a calculator or manually.
-
Result: Dividing 3.5 by 100 gives us 0.035. Therefore, 3.5% as a decimal is 0.035.
This simple two-step process provides the decimal equivalent of any percentage. Let's explore this further with some practical examples.
Practical Examples and Applications
The conversion of percentages to decimals has wide-ranging applications across various disciplines. Here are some examples illustrating the practical use of this conversion:
-
Finance and Investments: Calculating interest rates, returns on investments, and discounts often requires converting percentages to decimals. For instance, if an investment offers a 3.5% annual return, you would use 0.035 in your calculations to determine the actual monetary gain.
-
Statistics and Probability: In statistical analysis, percentages are often converted to decimals for easier computation of probabilities and other statistical measures. A probability of 3.5% would be represented as 0.035 in many statistical formulas.
-
Scientific Calculations: Many scientific formulas and equations involve percentages, and converting them to decimals is necessary for accurate calculations. For example, in chemistry, concentrations are often expressed as percentages, which need to be converted to decimals for calculations involving molarity or other concentration units.
-
Spreadsheet Software: Spreadsheet programs like Microsoft Excel or Google Sheets typically require decimal values for calculations. If you're working with percentages in a spreadsheet, you'll need to convert them to decimals to perform calculations accurately. The software might automatically handle the conversion in some cases, but understanding the underlying principle is still crucial for avoiding errors and understanding the results.
-
Data Analysis: When working with large datasets, converting percentages to decimals simplifies data manipulation and analysis. Many data analysis tools and programming languages work more efficiently with decimal numbers.
Beyond 3.5%: Converting Other Percentages
The method used to convert 3.5% to a decimal applies universally to any percentage. Let's illustrate this with a few more examples:
-
Converting 15% to a decimal: Remove the percentage sign (15) and divide by 100 (15/100 = 0.15). Therefore, 15% as a decimal is 0.15.
-
Converting 2.75% to a decimal: Remove the percentage sign (2.75) and divide by 100 (2.75/100 = 0.0275). Therefore, 2.75% as a decimal is 0.0275.
-
Converting 100% to a decimal: Remove the percentage sign (100) and divide by 100 (100/100 = 1). Therefore, 100% as a decimal is 1. This highlights that 100% represents the entire whole.
-
Converting 0.5% to a decimal: Remove the percentage sign (0.5) and divide by 100 (0.5/100 = 0.005). Therefore, 0.5% as a decimal is 0.005.
Alternative Method: Moving the Decimal Point
A quick alternative method for converting percentages to decimals involves moving the decimal point two places to the left. This is equivalent to dividing by 100. For example:
-
3.5%: Moving the decimal point two places to the left in 3.5 gives us 0.035.
-
15%: Moving the decimal point two places to the left in 15 (which is implicitly 15.0) gives us 0.15.
-
2.75%: Moving the decimal point two places to the left in 2.75 gives us 0.0275.
This shortcut can be very useful for quick mental calculations or estimations, but understanding the underlying principle of dividing by 100 remains crucial for a complete understanding.
Common Mistakes to Avoid
While the conversion process is straightforward, some common mistakes can occur:
-
Forgetting to divide by 100: This is the most common error. Remember that the crucial step is dividing the percentage value by 100 to obtain the decimal equivalent.
-
Incorrect placement of the decimal point: When using the decimal point shifting method, ensure you move the point exactly two places to the left.
-
Confusing percentages with decimals: Always remember the distinction between the two representations. A percentage is a fraction out of 100, while a decimal represents a number using a base-ten system.
Conclusion
Converting 3.5 percent to its decimal equivalent, 0.035, is a fundamental mathematical operation with far-reaching applications. Understanding this conversion is essential for anyone working with numerical data, whether in finance, statistics, science, or any field involving percentages. Mastering this skill will significantly improve accuracy and efficiency in various calculations. Remember the simple process: remove the percentage sign and divide by 100, or alternatively, move the decimal point two places to the left. By understanding these methods and avoiding common pitfalls, you can confidently convert percentages to decimals and unlock a deeper understanding of numerical data.
Latest Posts
Latest Posts
-
When Is Pcr Particularly Applicable
Sep 06, 2025
-
What Is A Sancho Food
Sep 06, 2025
-
What Is A Dialectical Shape
Sep 06, 2025
-
Where Can Utensils Be Stored
Sep 06, 2025
-
What Is 20 Of 780
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 3.5 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.