3 6 X 2 8
gasmanvison
Sep 22, 2025 · 6 min read
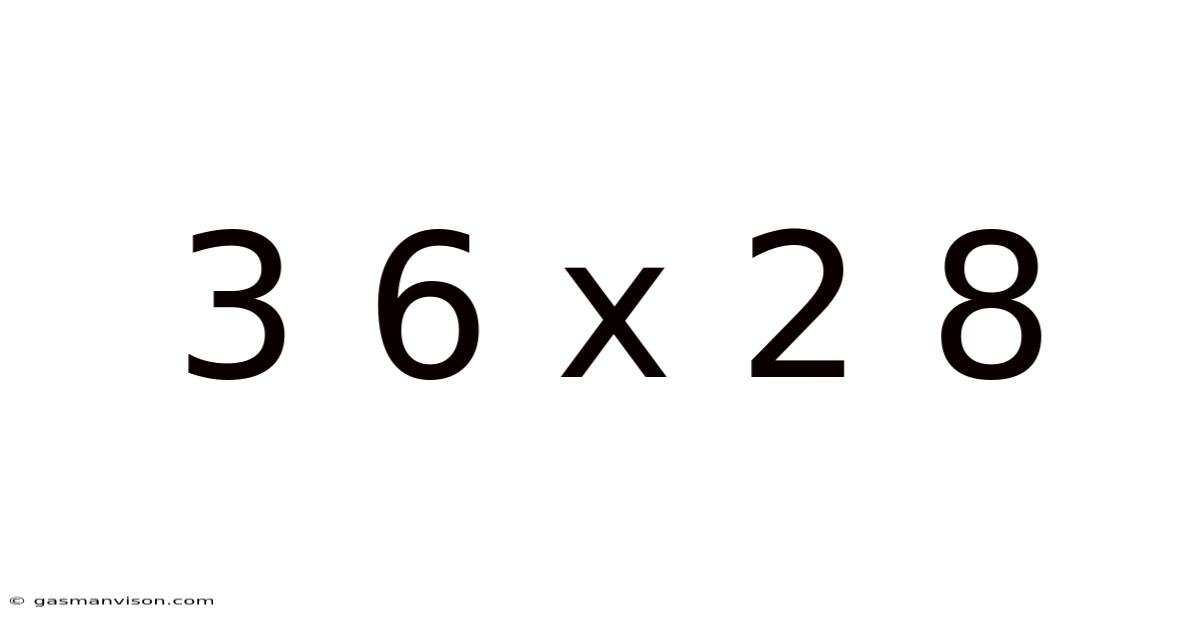
Table of Contents
Decoding 3.6 x 2.8: A Deep Dive into Dimensions, Applications, and Calculations
This article explores the seemingly simple dimensions "3.6 x 2.8," delving beyond the immediate numerical representation to uncover its various applications and the mathematical concepts surrounding it. While seemingly straightforward, understanding the context of these dimensions opens up a world of possibilities, from carpentry and construction to graphic design and data analysis. We'll explore how these dimensions are used, the calculations you can perform with them, and the broader implications within different fields.
What Does 3.6 x 2.8 Represent?
At its core, "3.6 x 2.8" represents a rectangular area or a volume depending on context. It defines a space with a length of 3.6 units and a width of 2.8 units. The "units" can vary widely: meters, centimeters, feet, inches, pixels, etc. The meaning drastically changes based on the context.
1. Applications in Construction and Carpentry:
In the building industry, 3.6 x 2.8 could represent the dimensions of:
- A door: A standard interior door might have these dimensions (in feet or meters), affecting the framing, hinges, and overall design. Accurate measurements are crucial for proper fitting and functionality. Consideration needs to be given to door swings and clearances.
- A window: Similarly, a window could have these dimensions, impacting the amount of natural light entering a room and the structural support required. The choice of materials, glazing, and frames would all relate to the dimensions.
- A section of flooring or wall: These dimensions could define the size of a specific area requiring tiling, painting, or paneling. Calculating material needs is crucial, including accounting for waste and overlapping.
- A foundation slab: While larger foundations are more typical, these dimensions could represent a small foundation for a shed or other outbuilding. The precise calculations of the volume and necessary materials depend on factors like depth and material type.
- Roofing materials: The dimensions might represent the size of a single roofing sheet, requiring calculations to determine how many sheets are needed for a particular roof area. The calculation would need to account for overlaps and waste.
2. Applications in Graphic Design and Digital Media:
In digital design, 3.6 x 2.8 might represent:
- Image dimensions: These could be the dimensions of an image in inches or centimeters, used for print media or web design. Resolution (DPI or PPI) is crucial in determining the final image quality.
- Canvas size: In digital art programs, these dimensions define the work area. Choosing the right size impacts the detail and file size of the final artwork.
- Banner ads: Web banner ads often adhere to specific size standards. These dimensions might fit certain ad placements, maximizing visibility and impact. Understanding the aspect ratio is key for optimal display.
- Video thumbnails: A video platform might use thumbnails with these dimensions to represent a larger video file. Optimizing thumbnail dimensions for various platforms is critical for engagement.
3. Applications in Data Analysis and Statistics:
While less directly apparent, these dimensions can play a role in:
- Data visualization: A scatter plot or graph might have these dimensions as the size of the plotting area. This influences the clarity and readability of the data representation.
- Data table dimensions: These numbers could represent rows and columns in a spreadsheet or database, reflecting the structure and scale of the dataset.
- Sampling areas: In scientific studies, 3.6 x 2.8 could represent the dimensions of a sampling area, used for collecting data or samples within a larger field. The method of sampling directly affects the conclusion.
Calculations Involving 3.6 x 2.8:
The core calculations involving these dimensions are centered around area and volume.
1. Area Calculation:
The most common calculation is finding the area of a rectangle using the formula:
- Area = Length x Width
In this case:
- Area = 3.6 x 2.8 = 10.08 square units
The units will depend on the context (square meters, square centimeters, square inches, etc.). This calculation is fundamental in numerous applications, from determining the amount of paint needed for a wall to calculating the size of a digital image.
2. Volume Calculation:
If a third dimension (height) is introduced, the calculation shifts to volume:
- Volume = Length x Width x Height
For example, if the height is 1.5 units:
- Volume = 3.6 x 2.8 x 1.5 = 15.12 cubic units
This calculation becomes relevant in applications like calculating the volume of a container, a room, or a building material. Understanding cubic units is important for accurate material ordering and project planning.
3. Aspect Ratio:
The ratio between the length and width (3.6:2.8) defines the aspect ratio. This is crucial in graphic design and video production to maintain consistent proportions when resizing or scaling. Simplifying the ratio gives a clearer understanding of the proportions: approximately 1.29:1. This aspect ratio is widely used in various media formats.
4. Perimeter Calculation:
The perimeter of a rectangle, the total distance around it, is calculated as:
- Perimeter = 2(Length + Width)
For 3.6 x 2.8:
- Perimeter = 2(3.6 + 2.8) = 12.8 units
This is useful for determining the length of fencing needed for a garden or the amount of molding for a room's perimeter.
5. Diagonal Calculation:
Using the Pythagorean theorem, we can find the diagonal length:
- Diagonal = √(Length² + Width²)
For 3.6 x 2.8:
- Diagonal = √(3.6² + 2.8²) ≈ 4.6 units
This calculation is essential in applications where the diagonal distance is relevant, such as calculating the length of a diagonal brace in construction or the distance across a rectangular screen.
Importance of Units and Context:
The critical factor in working with 3.6 x 2.8 is understanding the units. Without knowing whether the units are meters, centimeters, inches, or pixels, the calculations are meaningless. The context—construction, graphic design, or data analysis—dictates the appropriate units and the type of calculations required. Consistent use of units is paramount to avoid errors.
Beyond the Numbers: Practical Considerations:
Working with these dimensions often involves practical considerations beyond simple calculations:
- Tolerances: In construction, slight variations from the exact dimensions are acceptable within defined tolerances. These tolerances account for material imperfections and construction variations.
- Waste: Material waste is a factor to account for when ordering materials. Cutting and fitting processes often result in leftover material, which should be factored into the quantities ordered.
- Scalability: The ability to scale these dimensions up or down proportionally is important. Maintaining the aspect ratio is crucial in scaling for different applications.
- Material selection: The choice of materials significantly impacts the project cost and feasibility. The properties of different materials affect their suitability for specific applications.
Conclusion:
While the numbers 3.6 x 2.8 appear simple, their applications are diverse and require a comprehensive understanding of the context, units, and relevant calculations. From the precise measurements in construction to the creative dimensions in graphic design, these seemingly simple numbers underpin a vast array of processes and decisions. By understanding the calculations and practical implications, individuals can confidently apply these dimensions to various real-world situations, ensuring accuracy and efficiency. Accurate calculations and a keen awareness of the context are key to successful implementation across numerous fields.
Latest Posts
Latest Posts
-
Summer Break Plans 2 Paragraph
Sep 22, 2025
-
Identify The Suffix For Binding
Sep 22, 2025
-
Complete The Following Table Math
Sep 22, 2025
-
Metamorphism Involves The Addition Of
Sep 22, 2025
-
What 3 Things Cause Fires
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3 6 X 2 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.