3 7/8 As A Decimal
gasmanvison
Sep 25, 2025 · 5 min read
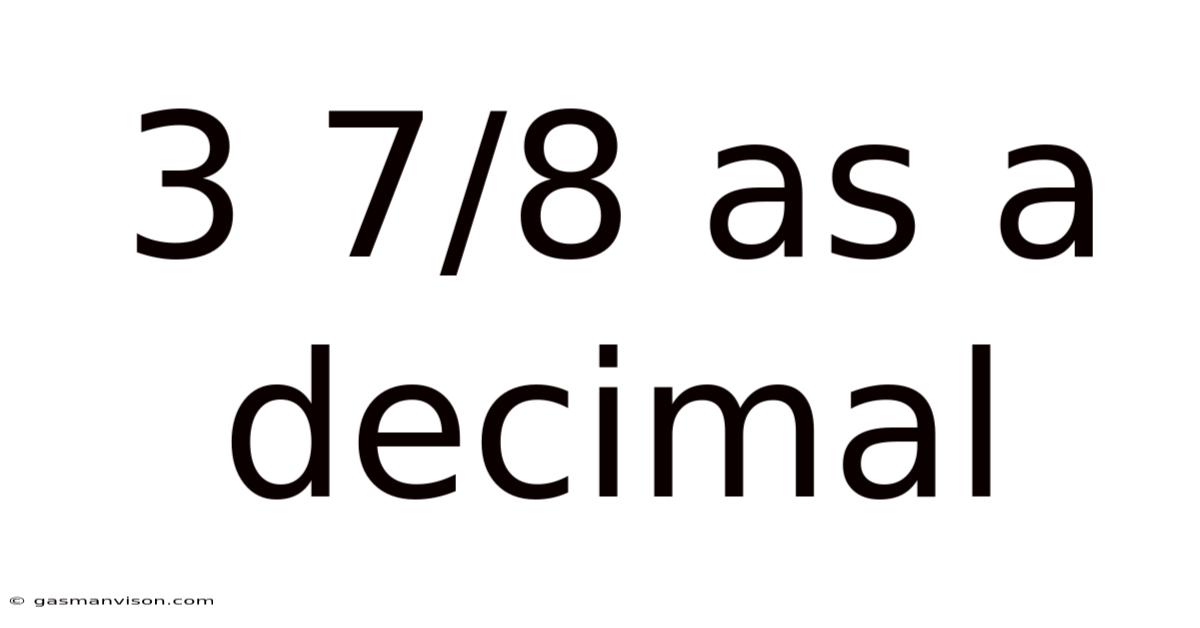
Table of Contents
3 7/8 as a Decimal: A Comprehensive Guide
Meta Description: Learn how to convert the mixed number 3 7/8 into its decimal equivalent. This comprehensive guide explains the process step-by-step, covers different methods, and explores related fraction-to-decimal conversions. Perfect for students, educators, and anyone needing a clear understanding of fraction-to-decimal conversion.
Converting fractions to decimals is a fundamental skill in mathematics with applications across numerous fields. Understanding this process is crucial for anyone working with numbers, from students tackling their math homework to professionals using data analysis in their careers. This article delves into the specific conversion of the mixed number 3 7/8 into its decimal equivalent, providing a thorough explanation and exploring various methods. We'll also touch upon related concepts and practical applications to solidify your understanding.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's briefly review the concepts of mixed numbers and decimals.
A mixed number combines a whole number and a fraction, like 3 7/8. It represents a value greater than one. The whole number (3 in this case) represents the number of whole units, while the fraction (7/8) represents a part of a whole unit.
A decimal, on the other hand, represents a number using a base-ten system. The digits to the right of the decimal point represent fractions of powers of ten (tenths, hundredths, thousandths, etc.). For example, 0.75 represents seventy-five hundredths (75/100).
The goal is to express the value represented by the mixed number 3 7/8 using the decimal system.
Method 1: Converting the Fraction to a Decimal, then Adding the Whole Number
This is arguably the most straightforward method. We'll first convert the fractional part (7/8) to a decimal and then add the whole number (3).
-
Divide the numerator by the denominator: To convert the fraction 7/8 to a decimal, divide the numerator (7) by the denominator (8).
7 ÷ 8 = 0.875
-
Add the whole number: Now, add the whole number part (3) to the decimal value we just calculated.
3 + 0.875 = 3.875
Therefore, 3 7/8 as a decimal is 3.875.
Method 2: Converting the Mixed Number to an Improper Fraction, then to a Decimal
This method involves first converting the mixed number into an improper fraction, and then converting that improper fraction into a decimal.
-
Convert to an improper fraction: To convert the mixed number 3 7/8 to an improper fraction, multiply the whole number (3) by the denominator (8), add the numerator (7), and place the result over the original denominator (8).
(3 * 8) + 7 = 24 + 7 = 31
The improper fraction is 31/8.
-
Divide the numerator by the denominator: Now, divide the numerator (31) by the denominator (8).
31 ÷ 8 = 3.875
Again, we arrive at the same result: 3 7/8 as a decimal is 3.875.
Method 3: Using Long Division (for a deeper understanding)
While the previous methods are quicker, understanding long division provides a deeper understanding of the conversion process. Let's walk through this method:
-
Set up the long division: Write 31 (from the improper fraction 31/8) inside the division symbol and 8 outside.
-
Divide: 8 goes into 31 three times (3 * 8 = 24). Write 3 above the division symbol.
-
Subtract: Subtract 24 from 31, leaving a remainder of 7.
-
Add a decimal point and a zero: Add a decimal point to the quotient (3) and add a zero to the remainder (7) to make it 70.
-
Continue dividing: 8 goes into 70 eight times (8 * 8 = 64). Write 8 after the decimal point in the quotient.
-
Subtract again: Subtract 64 from 70, leaving a remainder of 6.
-
Add another zero: Add another zero to the remainder (6) to make it 60.
-
Final division: 8 goes into 60 seven times (8 * 7 = 56). Write 7 after the 8 in the quotient.
-
Remainder: The remainder is 4. You can continue adding zeros and dividing to get more decimal places, but for practical purposes, we can stop here.
Therefore, the result is approximately 3.875. The slight discrepancies in the last digits may occur depending on the rounding employed in the long division.
Understanding Decimal Places and Rounding
The decimal representation of 3 7/8 is 3.875. This has three decimal places. Sometimes you might need to round the decimal to a specific number of decimal places. For example:
- Rounded to one decimal place: 3.9
- Rounded to two decimal places: 3.88
Rounding rules generally involve looking at the digit in the next decimal place. If it's 5 or greater, you round up; if it's less than 5, you round down.
Practical Applications
Understanding fraction-to-decimal conversions is crucial in various real-world applications:
- Cooking and Baking: Recipes often use fractions, but measuring tools usually display decimals.
- Engineering and Construction: Precise measurements are essential, and decimals are often preferred for accuracy.
- Finance: Calculating interest rates, discounts, and taxes frequently involves working with decimals.
- Data Analysis: Data is often presented in decimal form, requiring understanding of fractions for interpretation.
- Science: Many scientific measurements and calculations involve decimal representations of fractional values.
Similar Conversions
The method used to convert 3 7/8 to a decimal can be applied to other mixed numbers and fractions. For example:
- Converting 2 1/4 to a decimal: First, convert to an improper fraction (9/4), then divide (9 ÷ 4 = 2.25).
- Converting 1 3/5 to a decimal: First, convert to an improper fraction (8/5), then divide (8 ÷ 5 = 1.6).
Practice with various examples will solidify your understanding and improve your speed and accuracy.
Conclusion
Converting 3 7/8 to its decimal equivalent, 3.875, is a straightforward process that involves understanding fractions and decimals. This article presented several methods, from simple addition to detailed long division, allowing you to choose the method that best suits your understanding and needs. The ability to perform these conversions is a valuable skill across various fields, highlighting the importance of mastering this fundamental mathematical concept. Remember to practice regularly to build confidence and proficiency. By understanding the underlying principles and applying the different methods, you'll be well-equipped to tackle similar fraction-to-decimal conversions with ease.
Latest Posts
Latest Posts
-
75 Degrees C To F
Sep 25, 2025
-
Convert 175 Pounds To Kg
Sep 25, 2025
-
How To Find Slant Asymptotes
Sep 25, 2025
-
Unlike The Lithosphere The Asthenosphere
Sep 25, 2025
-
2x 6 4 X 3
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 7/8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.