3 Is 60 Of What
gasmanvison
Sep 19, 2025 · 5 min read
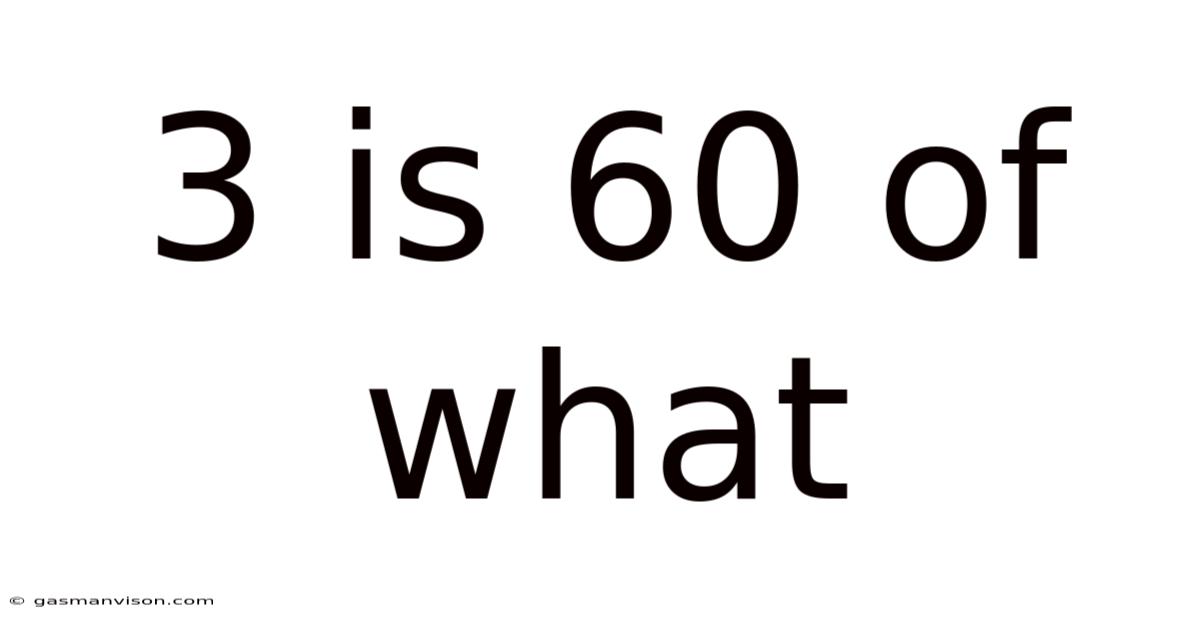
Table of Contents
3 is 60% of What Number? Unlocking the Power of Percentages
This seemingly simple question, "3 is 60% of what number?", masks a fundamental concept in mathematics with broad applications in everyday life. From calculating discounts and sales tax to understanding financial statements and statistical analyses, the ability to solve percentage problems is invaluable. This article will not only provide the solution but delve into the various methods for solving this problem, exploring different approaches and highlighting their practical uses. We'll also explore the broader context of percentages and their importance in various fields.
Understanding the Problem: Deconstructing the Percentage Equation
The core of this problem lies in understanding the relationship between a percentage, a part, and a whole. We're given that 3 represents 60% of an unknown number. To solve this, we need to translate this word problem into a mathematical equation. We can express this relationship as:
- Part = Percentage × Whole
In our case:
- Part = 3
- Percentage = 60% = 0.60 (Remember to convert percentages to decimals by dividing by 100)
- Whole = x (This is the unknown number we need to find)
Substituting these values into our equation, we get:
- 3 = 0.60x
Method 1: Solving the Equation Algebraically
This is the most straightforward approach. To isolate 'x', we need to divide both sides of the equation by 0.60:
- x = 3 / 0.60
- x = 5
Therefore, 3 is 60% of 5.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion where the ratio of the part to the whole is equal to the ratio of the percentage to 100%:
- 3/x = 60/100
Cross-multiplying, we get:
- 3 * 100 = 60 * x
- 300 = 60x
Dividing both sides by 60:
- x = 300 / 60
- x = 5
Again, we arrive at the same solution: 3 is 60% of 5.
Method 3: Working Backwards from the Percentage
This method involves understanding that 60% represents 60 parts out of 100. If 60 parts equal 3, we can find the value of one part by dividing 3 by 60:
- 1 part = 3 / 60 = 0.05
Since there are 100 parts in the whole, we multiply the value of one part by 100:
- Whole = 0.05 * 100 = 5
This confirms our previous solutions: 3 is 60% of 5.
Practical Applications: Real-World Scenarios Involving Percentages
Understanding how to solve percentage problems is crucial in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Imagine a store offers a 60% discount on an item. If the discounted price is $3, you can use this method to determine the original price.
-
Tax Calculations: If a sales tax of 60% adds $3 to the cost of an item, you can calculate the original price before tax.
-
Financial Analysis: Percentage changes are frequently used in finance to track growth or decline in investments, profits, or expenses. This skill helps in interpreting financial data effectively.
-
Statistical Data: Percentages are used extensively to represent proportions in data sets, allowing for clearer comparisons and interpretations of trends.
-
Surveys and Polls: Data from surveys and polls are frequently represented using percentages, enabling easier understanding of public opinion or preferences.
Beyond the Basics: Advanced Percentage Calculations
While the problem "3 is 60% of what number?" is a basic percentage problem, understanding it unlocks the ability to tackle more complex scenarios. Here are some advanced applications:
-
Compound Interest: Calculating compound interest involves repeatedly applying percentages over time. Understanding basic percentage calculations is fundamental to mastering this concept.
-
Percentage Increase and Decrease: Calculating percentage increases or decreases requires a good grasp of the underlying principles. This is crucial in various fields, including finance and economics.
-
Percentage Points: It's important to differentiate between percentage changes and percentage points. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
-
Working with Multiple Percentages: Many real-world problems involve multiple percentages. For instance, calculating a final price after multiple discounts or adding multiple taxes. Breaking down the problem into smaller, manageable percentage calculations is crucial for accuracy.
Tips and Tricks for Mastering Percentages:
-
Practice Regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
-
Use Different Methods: Experiment with different approaches to find the method that suits your understanding and problem-solving style best.
-
Visual Aids: Diagrams and charts can be helpful for visualizing percentage relationships, particularly when dealing with complex problems.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
-
Utilize Online Calculators (for verification, not primary solving): Online percentage calculators can be valuable tools for verifying your answers or assisting with more complex calculations, but always aim to understand the underlying principles before relying solely on calculators.
Conclusion: Mastering Percentages – A Key to Numerical Literacy
The ability to solve percentage problems, even seemingly simple ones like "3 is 60% of what number?", is a crucial skill for anyone navigating the modern world. From managing personal finances to understanding complex data, a strong grasp of percentages is essential for numerical literacy. By understanding the various methods and their applications, you can confidently tackle a wide range of percentage-related problems and unlock a deeper understanding of the numerical world around us. The seemingly simple question at the heart of this article reveals a pathway to a more profound understanding of mathematics and its practical relevance in everyday life. Mastering percentages empowers you to not only solve problems but also to interpret and analyze information with greater accuracy and confidence.
Latest Posts
Latest Posts
-
150kg Is How Many Pounds
Sep 19, 2025
-
Researchers On Car Safety Studied
Sep 19, 2025
-
Student Nonviolent Coordinating Committee Meaning
Sep 19, 2025
-
Cellular Respiration Formula In Words
Sep 19, 2025
-
What Is 50 Of 12
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 Is 60 Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.