3 Times What Equals 21
gasmanvison
Sep 19, 2025 · 5 min read
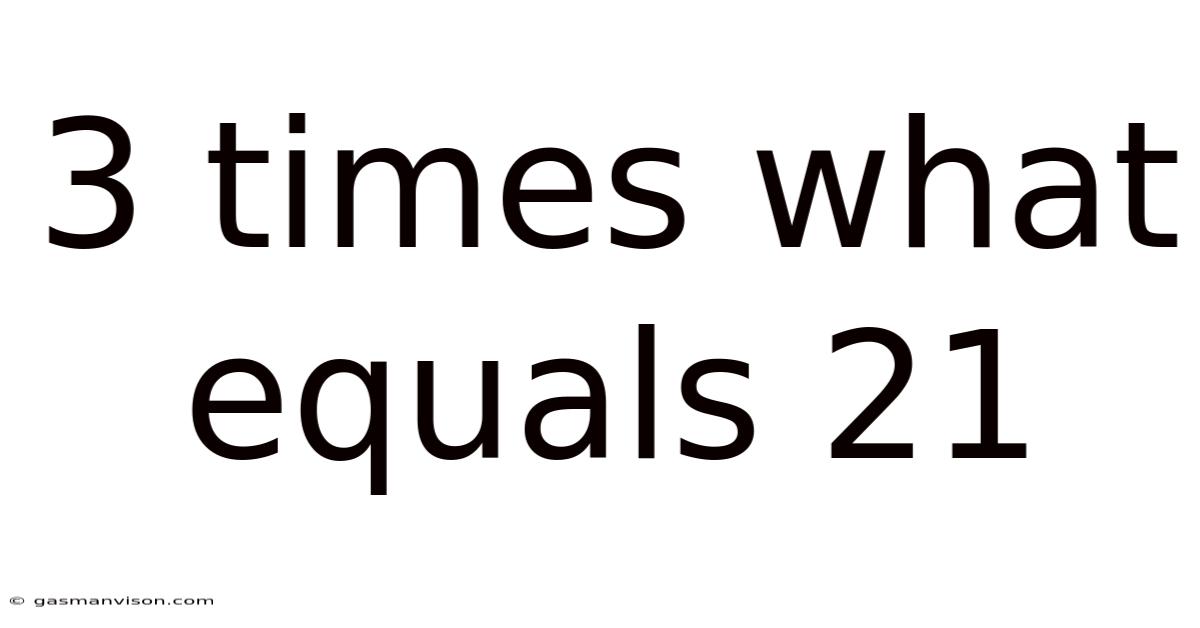
Table of Contents
Decoding "3 Times What Equals 21": A Deep Dive into Multiplication and its Applications
This seemingly simple question, "3 times what equals 21?", opens a door to a vast world of mathematical concepts and their real-world applications. While the immediate answer is easily calculated, understanding the underlying principles and exploring the diverse contexts in which this type of problem arises provides a richer learning experience. This article will not only solve the equation but delve into the broader mathematical landscape, exploring multiplication, its inverse operation (division), and its significance in various fields.
What is Multiplication?
Multiplication is a fundamental arithmetic operation representing repeated addition. It's a concise way of expressing the sum of several identical numbers. For instance, 3 x 4 (3 multiplied by 4) is the same as 3 + 3 + 3 + 3 = 12. The number being multiplied (3 in this case) is called the multiplicand, the number by which it's multiplied (4) is the multiplier, and the result (12) is the product.
Solving "3 Times What Equals 21"
The question "3 times what equals 21?" can be represented algebraically as:
3 * x = 21
Where 'x' represents the unknown number. To find the value of 'x', we employ the inverse operation of multiplication: division. We divide both sides of the equation by 3:
x = 21 / 3
Therefore, x = 7. So, the answer is 7. Three times seven equals twenty-one.
Beyond the Simple Solution: Exploring Division
The process of finding the answer highlights the crucial relationship between multiplication and division. They are inverse operations; one undoes the other. Understanding this relationship is essential for solving a wide array of mathematical problems. Division allows us to determine how many times one number is contained within another. In our example, division reveals that the number 3 is contained within 21 seven times.
Real-World Applications: Where Multiplication and Division Matter
The simple equation "3 times what equals 21?" might seem abstract, but its underlying principles are applied constantly in everyday life and across various disciplines:
1. Everyday Budgeting and Finance:
- Calculating total costs: Imagine buying three identical items. If the total cost is $21, dividing the total cost ($21) by the number of items (3) gives you the price of a single item ($7).
- Determining unit price: This is essential for comparing the value of different products. For example, comparing the cost per ounce of different cereals.
- Sharing expenses: If three friends split a $21 bill equally, each person pays $7.
2. Measurement and Conversions:
- Length conversions: Converting meters to centimeters (or vice versa) involves multiplication or division, depending on the direction of the conversion.
- Area calculations: Calculating the area of a rectangle requires multiplying its length and width. If you know the area and one dimension, you can use division to find the other.
- Volume calculations: Similar to area calculations, volume often involves multiplication (e.g., length x width x height for a rectangular prism).
3. Science and Engineering:
- Physics: Many physics formulas involve multiplication and division. For example, calculating speed (distance divided by time) or force (mass multiplied by acceleration).
- Chemistry: Stoichiometry, the study of the quantitative relationships between reactants and products in chemical reactions, relies heavily on multiplication and division.
- Engineering: Designing structures, calculating loads, and determining material requirements frequently utilize these operations.
4. Cooking and Baking:
- Scaling recipes: If a recipe calls for 3 cups of flour and you want to make a larger batch, you might multiply the ingredient amounts by a factor to increase the servings. Conversely, you might divide the ingredients to make a smaller portion.
- Determining ingredient ratios: Understanding ratios is crucial for baking, ensuring the right balance of ingredients.
5. Data Analysis and Statistics:
- Calculating averages: Finding the average (mean) of a dataset involves summing the values and then dividing by the number of values.
- Proportions: Understanding proportions is essential for making inferences and predictions from data.
- Percentages: Calculating percentages often involves multiplication and division.
6. Computer Programming:
- Looping: Many programming loops involve repeating a set of instructions a specific number of times, which directly relates to the concept of multiplication.
- Data manipulation: Data manipulation often involves performing mathematical operations, including multiplication and division, on datasets.
Expanding the Concept: Beyond Simple Multiplication
While "3 times what equals 21?" is a straightforward problem, it serves as a foundation for more complex mathematical concepts:
- Algebra: The algebraic representation of the problem (3 * x = 21) introduces the concept of variables and solving equations, a cornerstone of algebra.
- Ratio and Proportion: The problem can be expressed as a ratio: 3:21. Simplifying this ratio provides further understanding of the relationship between the numbers.
- Fractions and Decimals: The problem can also be expressed using fractions (3/21 = 1/7) or decimals (0.142857...), providing additional perspectives and problem-solving techniques.
Conclusion: The Enduring Significance of a Simple Equation
The seemingly simple question, "3 times what equals 21?", unlocks a world of mathematical understanding. It not only introduces the fundamental operation of multiplication and its inverse, division, but also demonstrates the ubiquitous nature of these operations across various fields. From everyday budgeting to complex scientific calculations, understanding multiplication and division empowers us to solve problems, make informed decisions, and appreciate the elegance and power of mathematics. The answer, 7, is more than just a numerical solution; it's a gateway to a deeper appreciation of the mathematical principles that shape our world. This deep understanding is not only valuable for academic pursuits but also crucial for navigating the complexities of daily life and professional endeavors. Mastering these fundamental concepts opens up a wide array of possibilities and empowers you to approach challenges with confidence and efficiency.
Latest Posts
Latest Posts
-
Cn Lewis Structure Molecular Geometry
Sep 19, 2025
-
Yellow Demarcation Bar Marking Indicates
Sep 19, 2025
-
Musical Composition With Recurring Refrain
Sep 19, 2025
-
Fluid Capacity For 4l60e Transmission
Sep 19, 2025
-
Whats The Capital Of Missouri
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.