3 Times What Equals 24
gasmanvison
Sep 25, 2025 · 6 min read
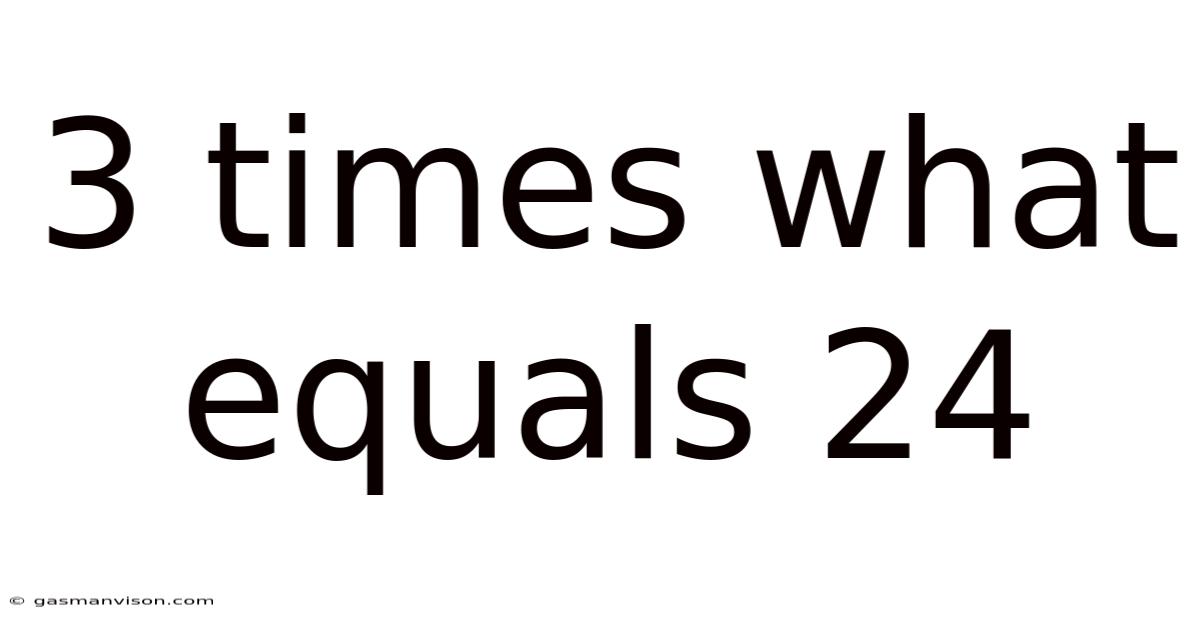
Table of Contents
3 Times What Equals 24? Exploring Multiplication and Problem-Solving Strategies
This seemingly simple question, "3 times what equals 24?", opens a door to a fascinating exploration of multiplication, problem-solving techniques, and even the broader world of mathematics. While the answer itself is straightforward, understanding the underlying concepts and the different ways to arrive at the solution offers valuable insights for students and anyone interested in enhancing their mathematical skills. This article delves into various approaches to solve this problem, discussing different mathematical concepts and offering practical applications.
Meta Description: Discover multiple ways to solve the equation "3 times what equals 24?". This comprehensive guide explores basic arithmetic, algebraic approaches, and real-world applications of this fundamental mathematical problem. Learn different problem-solving strategies and enhance your mathematical understanding.
Understanding the Basics of Multiplication
At its core, the question "3 times what equals 24?" is a simple multiplication problem. Multiplication is a fundamental arithmetic operation that represents repeated addition. In this case, we're looking for a number that, when multiplied by 3, results in a product of 24. This can be represented algebraically as:
3 * x = 24
Where 'x' represents the unknown number we need to find.
Method 1: Direct Division
The most straightforward method to solve this equation is through division. Since multiplication and division are inverse operations, we can isolate 'x' by dividing both sides of the equation by 3:
x = 24 / 3
This simplifies to:
x = 8
Therefore, 3 times 8 equals 24. This is the simplest and quickest method for solving this specific problem.
Method 2: Repeated Subtraction
While division is the most efficient, understanding the concept of multiplication as repeated addition allows us to solve this using repeated subtraction. We can repeatedly subtract 3 from 24 until we reach 0. The number of times we subtract 3 represents the solution.
24 - 3 = 21 21 - 3 = 18 18 - 3 = 15 15 - 3 = 12 12 - 3 = 9 9 - 3 = 6 6 - 3 = 3 3 - 3 = 0
We subtracted 3 a total of 8 times, confirming that 3 times 8 equals 24. This method, although less efficient than division, reinforces the relationship between multiplication and addition.
Method 3: Using Multiplication Tables
For smaller numbers, relying on memorized multiplication tables is a fast and effective approach. If you have memorized your multiplication facts, you'll instantly recognize that 3 multiplied by 8 equals 24. This method emphasizes the importance of memorization in building a strong foundation in mathematics. Knowing multiplication facts significantly speeds up calculations and improves problem-solving efficiency.
Method 4: Algebraic Approach
For more complex problems, an algebraic approach becomes necessary. We already established the equation:
3 * x = 24
To solve for 'x', we follow the principles of algebra. We divide both sides of the equation by 3 to isolate 'x':
(3 * x) / 3 = 24 / 3
This simplifies to:
x = 8
This method highlights the power of algebra in solving more intricate mathematical equations. It provides a systematic and structured way to tackle problems involving unknown variables.
Real-World Applications: Why is this important?
Understanding this simple equation, and the methods to solve it, has far-reaching applications in various real-world scenarios. Consider these examples:
-
Sharing equally: If you have 24 cookies and want to share them equally among 3 friends, you need to divide 24 by 3 to determine how many cookies each friend receives (8 cookies).
-
Calculating costs: If 3 apples cost $24, you divide $24 by 3 to find the cost of a single apple ($8).
-
Measuring quantities: If you need to cut a 24-meter long rope into 3 equal pieces, you divide 24 by 3 to determine the length of each piece (8 meters).
-
Scaling recipes: If a recipe calls for 3 cups of flour and you want to triple the recipe, you multiply 3 cups by 3 to get the required amount of flour (9 cups).
-
Unit Conversions: Converting units often involves multiplication and division. For instance, if 1 meter is equal to 100 centimeters, and you have 3 meters, you would multiply 3 by 100 to find the equivalent length in centimeters (300 centimeters).
These examples demonstrate the practicality and relevance of understanding multiplication and division in everyday life. Mastering these fundamental operations empowers you to tackle a wide range of problems effectively and efficiently.
Extending the Concept: Exploring More Complex Equations
While "3 times what equals 24?" is a relatively simple problem, it serves as a foundation for understanding more complex equations. Consider these variations:
-
3x + 5 = 29: This introduces an additional constant term. To solve, we first subtract 5 from both sides, then divide by 3. This requires a multi-step approach.
-
3x² = 75: This introduces a squared variable, requiring the use of square roots to solve for x.
-
3x / 4 = 6: This incorporates fractions, requiring an understanding of how to work with fractions in equations.
By gradually increasing the complexity of the equations, we build upon the foundational understanding gained from the simple "3 times what equals 24?" problem. This reinforces the importance of mastering basic arithmetic operations as a springboard for tackling more advanced mathematical concepts.
Problem-Solving Strategies: Beyond the Calculation
Solving mathematical problems effectively isn't just about finding the correct answer; it's also about developing strong problem-solving strategies. These strategies include:
-
Understanding the problem: Before attempting to solve, fully comprehend what the problem is asking. Identify the known variables and the unknown variable you need to find.
-
Choosing the right approach: Select the most efficient method based on the complexity of the problem. Sometimes, a simple approach like division is sufficient; other times, an algebraic approach is necessary.
-
Breaking down complex problems: For more challenging problems, break them down into smaller, more manageable steps. This makes the problem less daunting and easier to solve.
-
Checking your work: Always verify your answer to ensure its accuracy. Double-check your calculations and make sure your solution makes logical sense within the context of the problem.
These strategies are applicable not just to mathematical problems but to a wide range of problem-solving situations in life. They encourage a methodical and logical approach to tackling challenges, regardless of their nature.
Conclusion: The Power of Fundamentals
The seemingly simple question, "3 times what equals 24?", offers a rich opportunity to explore the fundamentals of multiplication, problem-solving techniques, and the practical applications of mathematics in everyday life. By understanding different approaches to solving this equation and applying various problem-solving strategies, we build a strong foundation for tackling more complex mathematical challenges and develop crucial skills applicable far beyond the realm of mathematics itself. Remember that mastering fundamental concepts is key to unlocking higher-level mathematical understanding and problem-solving abilities. The ability to confidently solve equations like this one is a stepping stone to more advanced mathematical concepts and a valuable skill for life.
Latest Posts
Latest Posts
-
Is 4 79 Rational Or Irrational
Sep 25, 2025
-
Safety Belts Are Designed To
Sep 25, 2025
-
Convert 9255 Cm3 To Gallons
Sep 25, 2025
-
Carbon Cycle Diagram Fill Question
Sep 25, 2025
-
These Take About 28 Days
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.