3 Times What Equals 36
gasmanvison
Sep 06, 2025 · 5 min read
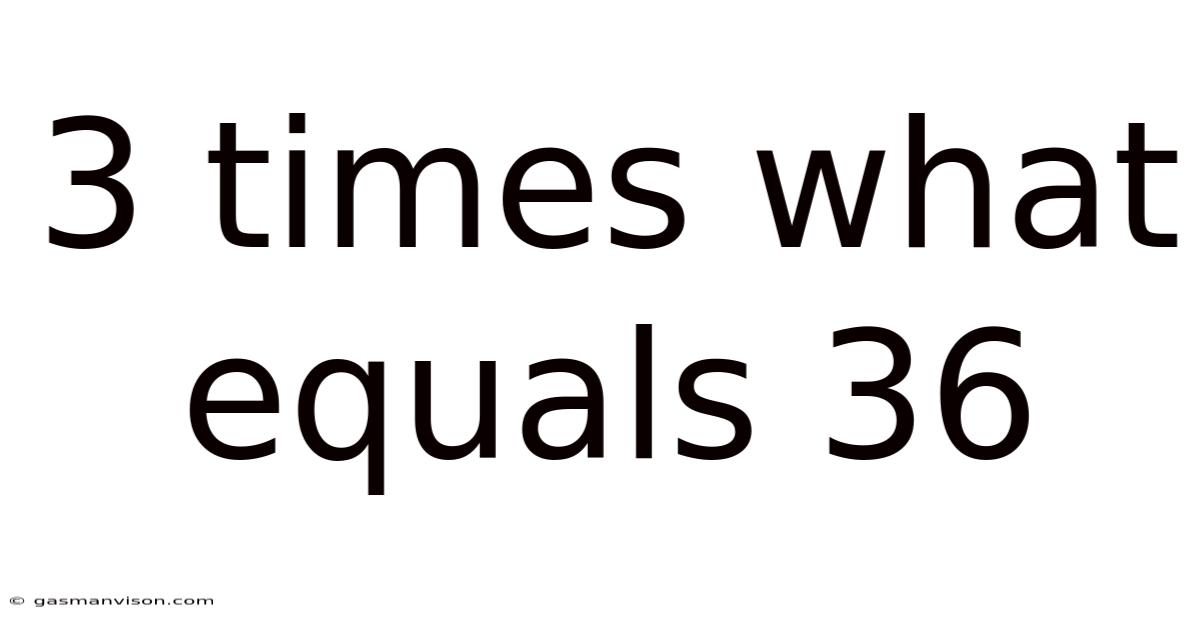
Table of Contents
Decoding 36: Unveiling the Multiplicative Pathways to 36
What number, multiplied by another, yields the intriguing product of 36? This seemingly simple question opens a door to a fascinating exploration of multiplication, factors, prime numbers, and even the elegance of mathematical patterns. This article delves deep into the various ways to arrive at 36 through multiplication, examining the different factor pairs and highlighting their significance in the broader context of mathematics.
Understanding Factors and Multiples
Before we delve into the specific combinations that result in 36, let's establish a firm understanding of key mathematical concepts. A factor is a number that divides another number exactly without leaving a remainder. Conversely, a multiple is a number obtained by multiplying a given number by an integer. In the context of our question, "3 times what equals 36?", we're looking for the factors of 36. We are essentially asking, "What number, when multiplied by 3, gives us 36?"
Finding the Factors of 36: A Systematic Approach
The most straightforward way to identify all the factors of 36 is to systematically consider all possible integer pairs whose product is 36. We can list these factor pairs as follows:
- 1 x 36: The simplest factor pair, representing the number itself and one.
- 2 x 18: Highlighting the divisibility of 36 by 2.
- 3 x 12: This is the answer to our initial question: 3 multiplied by 12 equals 36.
- 4 x 9: Demonstrating the divisibility of 36 by both 4 and 9.
- 6 x 6: A unique pair where both factors are identical, indicating that 36 is a perfect square.
This systematic approach ensures we don't miss any factor pairs. We can see that 36 has a relatively large number of factors, reflecting its composite nature.
Prime Factorization: Breaking Down 36 into its Prime Components
A crucial concept in number theory is prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Prime factorization involves expressing a number as a product of its prime factors. Let's find the prime factorization of 36:
36 can be initially broken down into 6 x 6. However, 6 is not a prime number; it can be further factored as 2 x 3. Therefore, the prime factorization of 36 is 2 x 2 x 3 x 3, which can also be written as 2² x 3². This representation is unique to 36 and provides fundamental insights into its properties. Understanding prime factorization is critical in various mathematical applications, including cryptography and data compression.
Exploring the Relationships Between Factors
The factor pairs of 36 reveal interesting relationships. Notice that as one factor increases, the other decreases. This inverse relationship is a characteristic of all factor pairs. Also, observe that the factors are not randomly distributed; they exhibit patterns and symmetries. This regularity is a testament to the underlying structure of the number system.
The fact that 36 has multiple factor pairs leads to various possible mathematical equations. For instance, we can use the factors to create different expressions, all resulting in 36. Consider the following examples:
- Addition: 18 + 18 = 36; 12 + 12 + 12 = 36; 9 + 9 + 9 + 9 = 36
- Subtraction: 72 - 36 = 36; 100 - 64 = 36
- Exponents: 6² = 36; (√36)² = 36
These examples highlight the versatility of 36 and its connections to various arithmetic operations.
36 in Geometry and Other Mathematical Contexts
The number 36 appears in various geometric and mathematical contexts:
-
Squares and Rectangles: A square with sides of 6 units has an area of 36 square units. Similarly, rectangles with dimensions of 4 x 9 or 3 x 12 also have areas of 36 square units. This connection highlights the relationship between multiplication and area calculation.
-
Hexagons: A regular hexagon can be divided into six equilateral triangles. If each triangle has an area of 6 square units, the total area of the hexagon would be 36 square units.
-
Number Theory: 36 is a highly composite number, meaning it has more divisors than any smaller positive integer. This property underscores its significance in number theory.
-
Calendar: 36 is a significant number related to the number of days in some lunar calendars.
The Significance of Factors in Real-World Applications
Understanding factors extends beyond the realm of theoretical mathematics. It finds practical applications in various fields:
-
Division and Sharing: When distributing items evenly among groups, understanding the factors of the total number is crucial. For example, 36 items can be equally divided among 2, 3, 4, 6, 9, or 12 groups.
-
Measurement and Design: In construction and design, factors play a vital role in optimizing dimensions and layouts. Knowing the factors of a given area facilitates efficient arrangement and resource allocation.
-
Data Analysis: The concept of factors is crucial in statistical analysis and data processing, where data is often categorized and analyzed based on its factors or attributes.
Conclusion: Beyond the Simple Equation
The seemingly simple question, "3 times what equals 36?" opens the door to a wealth of mathematical concepts and applications. By exploring the factors of 36, we've touched upon prime factorization, perfect squares, geometrical interpretations, and real-world applications. The number 36, seemingly ordinary, reveals a hidden richness when viewed through the lens of mathematical inquiry. This exploration underscores the interconnectedness of mathematical ideas and the surprising depth contained within seemingly simple numerical problems. Understanding these fundamental concepts lays a solid foundation for tackling more complex mathematical challenges and for appreciating the elegance and practicality of mathematics in our world.
Latest Posts
Latest Posts
-
I Hate You In Spanish
Sep 06, 2025
-
Is 1 4 Bigger Than 1 8
Sep 06, 2025
-
Is Cl2o Polar Or Nonpolar
Sep 06, 2025
-
What Problem Is Being Modeled
Sep 06, 2025
-
Ustedes Son De Puerto Rico
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.