3 Times What Equals 4
gasmanvison
Sep 19, 2025 · 5 min read
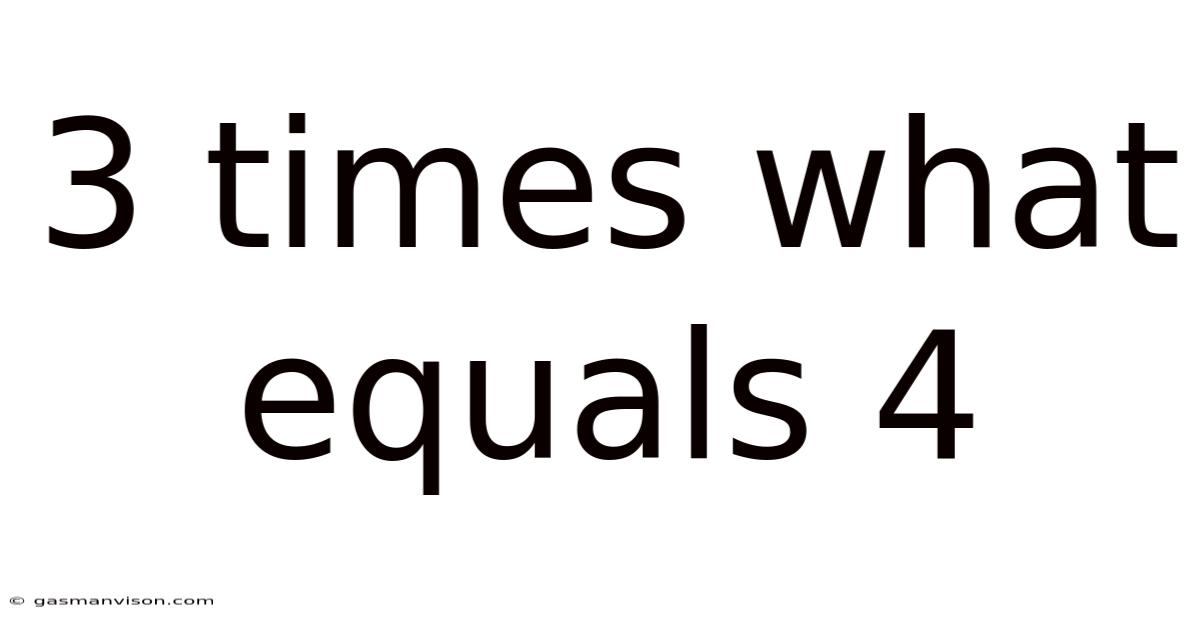
Table of Contents
3 Times What Equals 4? Unveiling the Mathematical Mystery and Its Real-World Applications
This seemingly simple question, "3 times what equals 4?", hides a deeper mathematical concept that extends far beyond basic arithmetic. It's a gateway to understanding fractions, equations, and even more complex algebraic principles. This article will delve into the solution, explore its significance, and illustrate its application in various real-world scenarios. We'll unravel the mystery step-by-step, making this concept accessible to everyone, from elementary school students to seasoned mathematicians.
Understanding the Problem: A Simple Equation
The question "3 times what equals 4" can be expressed as a simple algebraic equation: 3x = 4. Here, 'x' represents the unknown value we're trying to find. The equation states that three times an unknown number (x) results in 4. Solving this equation involves isolating 'x' to find its value.
Solving the Equation: Finding the Value of x
To isolate 'x', we need to perform the inverse operation of multiplication, which is division. We divide both sides of the equation by 3:
3x / 3 = 4 / 3
This simplifies to:
x = 4/3
Therefore, the answer to "3 times what equals 4" is 4/3, or one and one-third (1 1/3). This is a simple fraction representing the exact value. It's crucial to understand that this is not a whole number; it's a rational number, a number that can be expressed as a fraction.
Beyond the Basics: Exploring Fractions and Decimals
The solution, 4/3, is a fraction. Fractions represent parts of a whole. In this case, 4/3 represents four parts of a whole that is divided into three equal parts. It's greater than one whole because the numerator (4) is larger than the denominator (3).
We can also express 4/3 as a decimal. To do this, we simply divide 4 by 3:
4 ÷ 3 = 1.333...
The decimal representation of 4/3 is a recurring decimal, meaning the digit 3 repeats infinitely. We often round this to 1.33 for practical purposes, but it's important to remember that it's not an exact representation.
Real-World Applications: Where This Concept Matters
While seemingly abstract, the concept of solving equations like 3x = 4 has numerous practical applications in everyday life and various professions:
1. Recipe Scaling: Imagine you have a recipe that calls for 3 cups of flour, but you only want to make a smaller portion. If the recipe yields 4 servings, and you want only one serving, you need to find out how much flour to use. This problem translates to 3x = 4/3 or x= 4/9 of a cup of flour to make just one serving instead of four servings.
2. Unit Conversion: Let's say you're working with a project that requires 4 meters of material, but your measurements are in yards. If 1 yard is approximately equal to 0.9144 meters, you would need to solve an equation to find out how many yards you need. This conversion involves using the same principle as the original problem.
3. Budgeting and Finance: If you want to save a total of $400 over three months, you need to calculate how much money to save each month. This is again represented by the equation 3x = 400, where x is the amount to save per month. Solving for x, we find x = 400/3 ≈ $133.33 per month.
4. Engineering and Physics: Many engineering and physics problems involve solving equations to find unknown variables. For instance, calculating the force required to accelerate an object or determining the resistance in an electrical circuit often uses similar principles.
5. Construction and Design: Dividing resources such as concrete, materials, and time frequently requires the same arithmetic principles. In constructing a structure, if 4 units of material are required for a job and this job must be completed in 3 days, then each day requires approximately 1.33 units of the material.
6. Data Analysis and Statistics: Solving equations like 3x = 4 is fundamental in statistical calculations, particularly when dealing with proportions, means, and averages.
Expanding the Concept: More Complex Equations
Understanding the solution to 3x = 4 lays the foundation for tackling more complex algebraic equations. These equations might involve multiple variables, exponents, or other mathematical operations. However, the underlying principle of performing inverse operations to isolate the unknown variable remains the same.
For example, consider the equation 3x + 5 = 11. To solve for x, we first subtract 5 from both sides, resulting in 3x = 6. Then, we divide both sides by 3 to find x = 2. This slightly more complex example demonstrates that the core principles remain constant even with added elements.
Connecting to Higher-Level Mathematics:
The solution to 3x = 4, and the process of solving it, is fundamental to many areas of advanced mathematics. It's crucial in:
-
Calculus: Derivatives and integrals involve working with rates of change and areas under curves. Understanding basic equation solving is essential for manipulating and interpreting these concepts.
-
Linear Algebra: Systems of linear equations are solved using techniques that build directly upon the principles of solving single-variable equations.
-
Differential Equations: Solving differential equations, which model many real-world phenomena, relies heavily on the fundamental principles explored here.
Conclusion: The Enduring Importance of a Simple Equation
The question, "3 times what equals 4?", while simple in its phrasing, opens a window into the world of mathematics. The solution, 4/3, is not just a number; it's a concept that demonstrates the power of algebraic thinking and its widespread applicability in various aspects of our lives. From scaling recipes to complex engineering calculations, understanding how to solve this type of equation is a valuable skill that transcends the boundaries of the classroom and extends into the real world. Mastering this fundamental concept provides a solid foundation for tackling more complex mathematical challenges and fostering a deeper appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
How Much Is 45 Ml
Sep 19, 2025
-
Increasing And Decreasing Intervals Calculator
Sep 19, 2025
-
28 Grams In An Ounce
Sep 19, 2025
-
4 3 On Number Line
Sep 19, 2025
-
Definition Of A Character Trait
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.