35 56 In Simplest Form
gasmanvison
Sep 14, 2025 · 5 min read
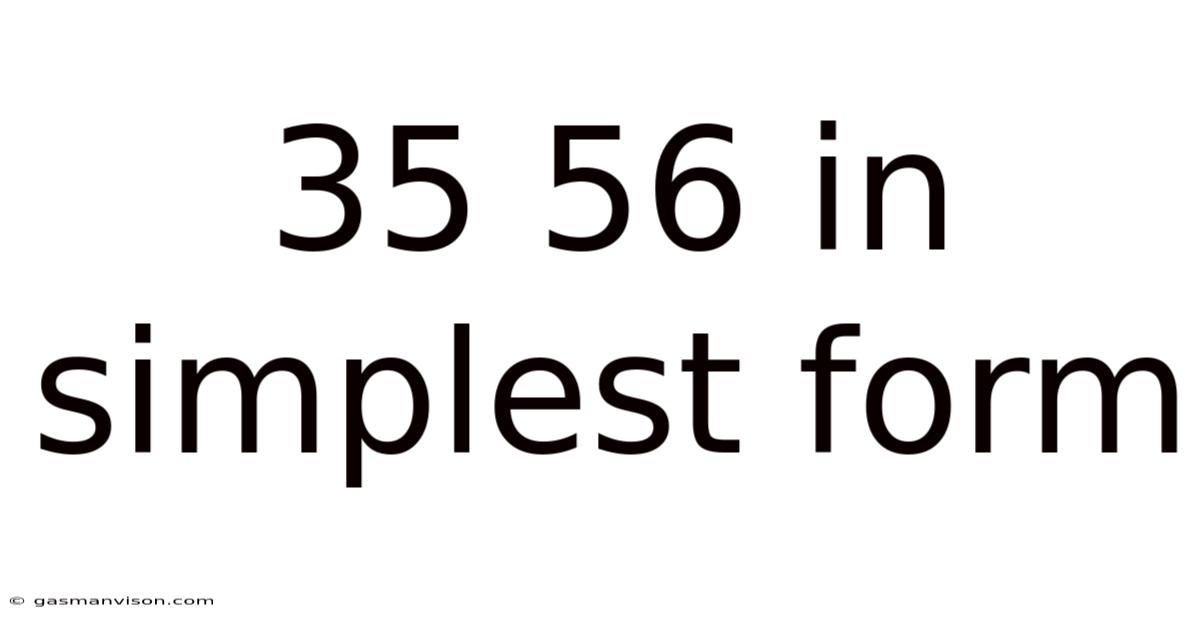
Table of Contents
Simplifying Fractions: A Deep Dive into 35/56
This article provides a comprehensive guide to simplifying the fraction 35/56, explaining the process in detail and exploring the underlying mathematical concepts. We'll cover finding the greatest common divisor (GCD), applying the simplification process, and even delve into why simplifying fractions is important in mathematics and beyond. Understanding this seemingly simple task unlocks a deeper appreciation for fundamental mathematical principles.
Meta Description: Learn how to simplify the fraction 35/56 step-by-step. This guide explains the concept of greatest common divisor (GCD), provides multiple methods for finding it, and clarifies why fraction simplification is crucial in math.
Understanding Fractions and Simplification
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The fraction 35/56 means 35 parts out of a total of 56 parts. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it simply represents it in a more concise and manageable form.
Think of a pizza cut into 56 slices. If you have 35 slices, you have 35/56 of the pizza. Simplifying the fraction doesn't change the amount of pizza you have; it just expresses the proportion in a simpler way.
Finding the Greatest Common Divisor (GCD)
The key to simplifying fractions lies in finding the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. There are several methods to find the GCD:
1. Listing Factors Method:
This method involves listing all the factors of both the numerator (35) and the denominator (56). The factors are the numbers that divide evenly into the given number.
- Factors of 35: 1, 5, 7, 35
- Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
The common factors are 1 and 7. The greatest of these common factors is 7. Therefore, the GCD of 35 and 56 is 7.
2. Prime Factorization Method:
This method involves breaking down the numerator and denominator into their prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 35: 5 x 7
- Prime factorization of 56: 2 x 2 x 2 x 7 (or 2³ x 7)
The common prime factor is 7. The GCD is the product of the common prime factors, which in this case is simply 7.
3. Euclidean Algorithm:
The Euclidean algorithm is a more efficient method for finding the GCD, especially for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 56 by 35: 56 ÷ 35 = 1 with a remainder of 21.
- Divide 35 by 21: 35 ÷ 21 = 1 with a remainder of 14.
- Divide 21 by 14: 21 ÷ 14 = 1 with a remainder of 7.
- Divide 14 by 7: 14 ÷ 7 = 2 with a remainder of 0.
The last non-zero remainder is 7, so the GCD of 35 and 56 is 7.
Simplifying 35/56
Now that we've established that the GCD of 35 and 56 is 7, we can simplify the fraction:
Divide both the numerator and the denominator by the GCD (7):
35 ÷ 7 = 5 56 ÷ 7 = 8
Therefore, the simplified form of 35/56 is 5/8.
Why Simplify Fractions?
Simplifying fractions is important for several reasons:
-
Clarity and Understandability: Simplified fractions are easier to understand and work with. 5/8 is much clearer than 35/56.
-
Easier Calculations: Simplified fractions make calculations simpler, especially when adding, subtracting, multiplying, or dividing fractions.
-
Consistent Representation: Simplifying ensures a consistent representation of a fraction's value. Multiple fractions can represent the same value (e.g., 1/2, 2/4, 3/6), but only one is in its simplest form.
-
Problem Solving: In many mathematical problems, simplifying fractions is a crucial step towards finding the solution. It simplifies complex expressions and reveals patterns more easily.
Applications of Fraction Simplification
Fraction simplification is not just a theoretical exercise; it has practical applications in various fields:
-
Cooking and Baking: Recipes often use fractions, and simplifying them helps in accurate measurements.
-
Construction and Engineering: Calculations involving measurements and proportions frequently require simplified fractions for precision.
-
Finance: Working with percentages and ratios often involves simplifying fractions to understand proportions and relationships.
-
Data Analysis: Simplifying fractions helps in interpreting data and presenting it in a clear and concise manner.
Beyond 35/56: Practicing Fraction Simplification
Understanding how to simplify 35/56 provides a solid foundation for simplifying other fractions. Here are some tips for practicing:
-
Master the GCD methods: Become proficient in finding the GCD using different methods. Choose the method that you find easiest and most efficient.
-
Practice with various fractions: Try simplifying different fractions with varying degrees of complexity.
-
Check your work: Always verify your simplified fraction by ensuring that the numerator and denominator have no common factors other than 1.
-
Use online resources: Numerous online calculators and tutorials can help you practice and check your understanding.
By consistently practicing and applying these methods, you'll build confidence and competence in simplifying fractions, a fundamental skill in mathematics and many other areas. Remember, the key is to find the greatest common divisor and then divide both the numerator and denominator by that number. This seemingly simple process unlocks a deeper understanding of mathematical principles and enhances problem-solving abilities.
Latest Posts
Latest Posts
-
Unproctored Placement Assessment Answer Key
Sep 14, 2025
-
Scientific Name For A Sheep
Sep 14, 2025
-
Which Term Describes An Enzyme
Sep 14, 2025
-
Formula For Mercury Ii Oxide
Sep 14, 2025
-
48 Degrees Farenheit To Celcius
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 35 56 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.