3x 2 5x 8 0
gasmanvison
Sep 14, 2025 · 5 min read
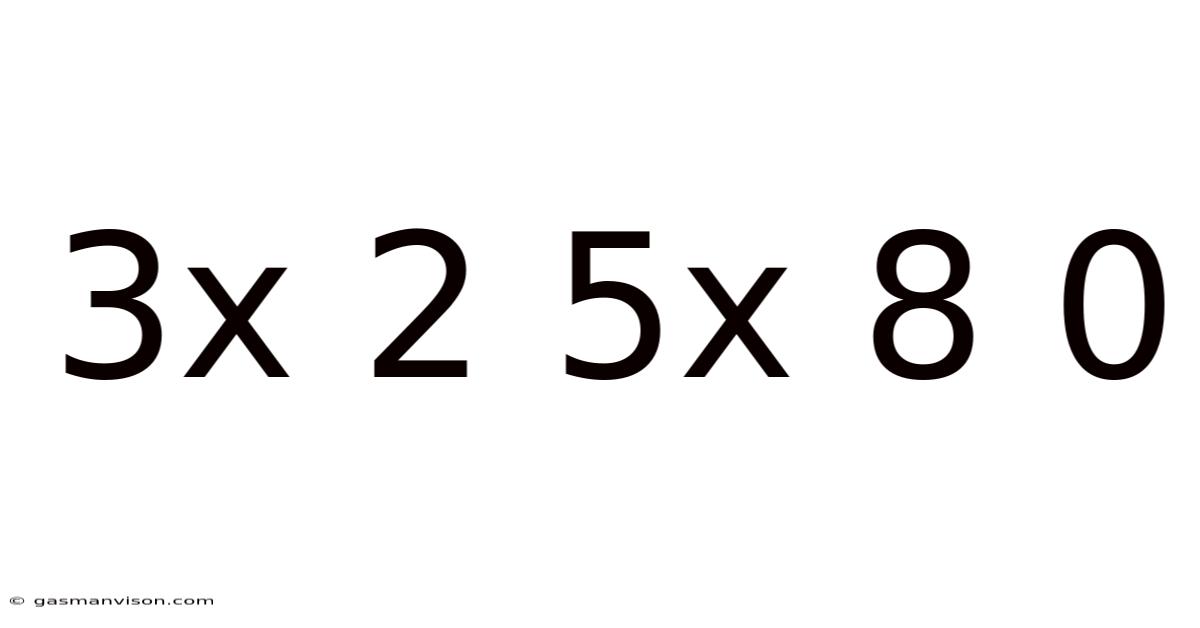
Table of Contents
Decoding the Mysterious Sequence: 3x 2 5x 8 0 – A Deep Dive into Pattern Recognition and Mathematical Possibilities
This seemingly random sequence, "3x 2 5x 8 0," presents a fascinating challenge. It's a puzzle that can be approached from numerous angles, each revealing a different perspective on pattern recognition, mathematical operations, and the creative process of problem-solving. This article explores various interpretations and potential underlying structures, emphasizing the importance of logical reasoning and systematic exploration in deciphering such sequences. Let's delve into the possibilities.
What Makes This Sequence Intriguing?
The immediate impression is ambiguity. The use of "x" introduces uncertainty; is it a multiplication symbol, a variable, or something else entirely? The lack of clear operators between the numbers further complicates the situation. This inherent ambiguity allows for multiple interpretations, making it an excellent example of how a seemingly simple sequence can lead to complex analytical explorations. The apparent randomness sparks curiosity, pushing us to seek order amidst the chaos. This exploration directly relates to core concepts in mathematics, data analysis, and even cryptography.
Possible Interpretations and Mathematical Approaches:
Let's examine different perspectives on this sequence:
1. The Multiplication Hypothesis:
If "x" represents multiplication, we have: 3 * 2 = 6, 5 * 8 = 40. This leaves us with the sequence 6, 40, 0. This interpretation is straightforward but doesn't reveal any readily apparent pattern. Further investigation is necessary. We could explore:
- Differences: Calculating the difference between consecutive terms (40 - 6 = 34). This difference doesn't immediately reveal a pattern, but it's a valuable step in pattern recognition.
- Ratios: Examining the ratio between consecutive terms (40/6 ≈ 6.67). Again, no immediately obvious pattern emerges.
- Higher-Order Differences: Calculating the differences between the differences might reveal a pattern, but in this case, it's unlikely to yield a clear result.
- Progression Types: Considering arithmetic progressions (constant difference), geometric progressions (constant ratio), or other types of numerical sequences is crucial. This sequence doesn't appear to follow any standard mathematical progression.
2. The Variable Hypothesis:
If "x" represents a variable, then the sequence represents a set of equations or data points. For instance, it could be interpreted as:
- Coordinate Points: The sequence might represent three coordinate points in a 2D or 3D space. (3, 2), (5, 8), and (0, y) where "y" is an unknown. This interpretation requires additional information or context to be meaningful. Further exploration might involve plotting these points to visually identify any patterns or relationships. This approach draws upon concepts of geometry and coordinate systems.
- Polynomial Equation: The sequence might be a subset of a larger polynomial equation where "x" is the independent variable and the numbers represent dependent values. Finding the polynomial equation that fits these points would require advanced mathematical methods. This interpretation brings in concepts of algebra and polynomial interpolation.
- System of Equations: If additional context or equations are provided, this sequence could be part of a larger system of equations that could be solved simultaneously. This approach directly utilizes algebraic principles and techniques for solving simultaneous equations.
3. The Alternate Operator Hypothesis:
Could the "x" represent a different operator? This interpretation requires a degree of creativity and possibly some outside knowledge or context. Potentially:
- Concatenation: If "x" represents concatenation (joining strings together), we get "32580," which doesn't immediately suggest a mathematical or numerical pattern. However, this could be part of a larger code or cipher.
- Custom Operators: It’s possible that "x" represents a newly defined mathematical operation. Without knowing the definition of this operator, however, this interpretation is impossible to solve. This highlights the role of clearly defined symbols and operators in mathematical communication.
4. The Contextual Hypothesis:
The most significant aspect of solving this puzzle might lie in the context from which it originated. Without knowing the source, it's difficult to definitively interpret the sequence. For instance:
- Code or Cipher: The sequence could be part of a code or cipher, particularly if it originated from a security or cryptography-related setting. The sequence could represent a key or a piece of encrypted data.
- Real-World Data: The sequence might represent measurements, observations, or data points from a scientific experiment, engineering project, or other real-world scenario. Understanding the context would be paramount to deciphering the sequence.
- Puzzle or Riddle: The sequence could be a component of a larger puzzle or riddle that provides additional clues or context to aid in its solution.
Expanding the Investigation:
To fully analyze this sequence, we need to consider:
- Additional Data: More numbers in the sequence would significantly aid in pattern recognition. Additional data points provide more opportunities to identify patterns and relationships.
- Contextual Clues: Understanding the origin and purpose of the sequence would provide vital information for interpretation. Context offers direction and prevents fruitless speculation.
- Advanced Techniques: Techniques like Fourier analysis, wavelet transforms, and other signal processing methods could be used to identify hidden patterns within the sequence if it represents a signal or a time series.
- Computational Methods: Computational approaches, such as machine learning algorithms, could be employed to identify patterns or make predictions based on the sequence. This approach allows for exploring more complex patterns that might not be apparent through manual analysis.
Conclusion: The Power of Ambiguity and Systematic Approach
The sequence "3x 2 5x 8 0" is a potent example of how seemingly simple puzzles can lead to complex and rewarding explorations in mathematics and logic. The ambiguity inherent in the sequence demands a systematic approach, requiring us to consider numerous possibilities and employ diverse analytical techniques. The ultimate solution depends heavily on the context, but the process of exploring different interpretations highlights the importance of creative thinking, logical reasoning, and the power of systematic investigation in problem-solving. It encourages us to think critically, experiment with different approaches, and understand that the solution might lie not just in the numbers themselves, but also in the context surrounding them. This problem serves as a valuable reminder that the most challenging puzzles often reward the most diligent and creative minds. The journey of exploring this sequence is as valuable as any definitive solution that might eventually be found.
Latest Posts
Latest Posts
-
What Is 72kg In Pounds
Sep 14, 2025
-
Pb So4 2 Compound Name
Sep 14, 2025
-
Ancient River Valley Civilizations Map
Sep 14, 2025
-
Instructors Who Might Greet Namaste
Sep 14, 2025
-
What Times What Equals 96
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 5x 8 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.