4 5n 7 10n 2
gasmanvison
Sep 23, 2025 · 6 min read
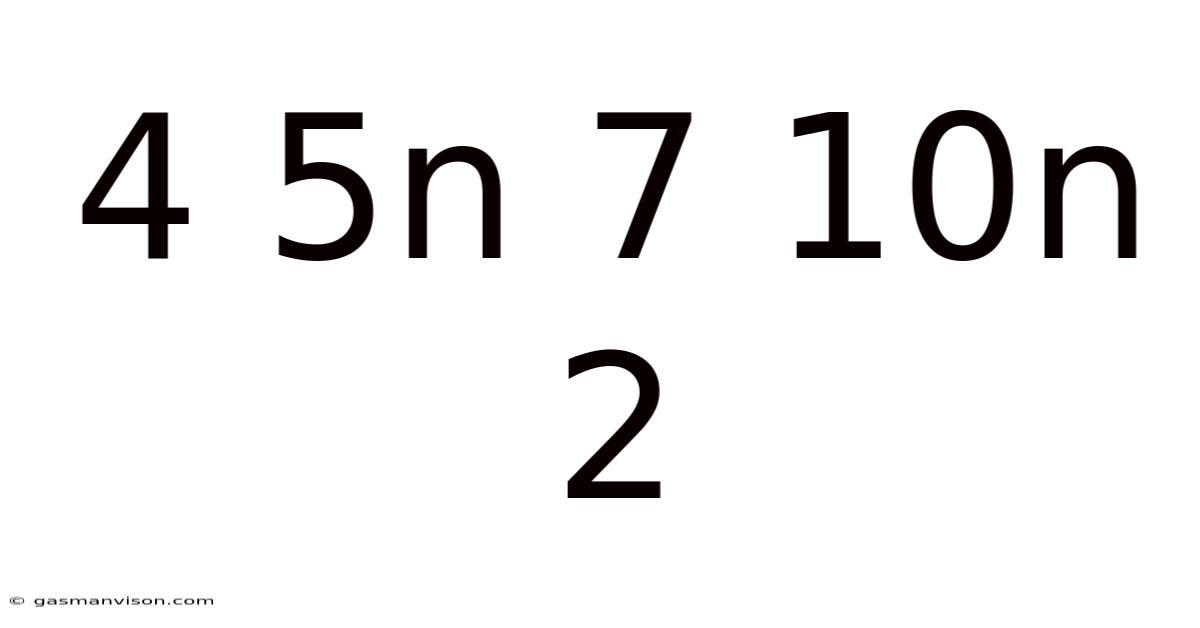
Table of Contents
Decoding the Enigmatic Sequence: 4, 5n, 7, 10n, 2 – A Deep Dive into Pattern Recognition and Mathematical Logic
This article delves into the seemingly random sequence: 4, 5n, 7, 10n, 2. We'll explore various approaches to understanding the underlying pattern, examining different mathematical concepts and logical reasoning to decipher its structure. While the sequence itself lacks immediate obviousness, the journey of uncovering its potential logic is an engaging exploration into the world of number patterns and mathematical thinking. Understanding this type of sequence enhances analytical skills vital for problem-solving in various fields, including computer science, data analysis, and cryptography.
The initial appearance of this sequence suggests a lack of immediate coherence. Numbers alternate between integers and expressions involving "n," denoting an unknown variable. This ambiguity necessitates a multi-faceted approach, considering several possibilities:
1. Interpreting 'n' as a Variable: Exploring Potential Mathematical Relationships
The presence of 'n' suggests a potential algebraic relationship. One approach is to treat 'n' as a variable and attempt to find a formula that generates the sequence. This requires identifying potential relationships between the known terms: 4, 7, and 2. Let's consider the differences and ratios between these numbers:
- Differences: The differences between consecutive integer terms are not consistent (7 - 4 = 3, 2 - 7 = -5). This rules out a simple arithmetic progression.
- Ratios: The ratios between consecutive integer terms are also inconsistent (7/4 = 1.75, 2/7 ≈ 0.28). This eliminates a simple geometric progression.
Given the lack of simple arithmetic or geometric patterns, let's explore more complex relationships. Could the 'n' terms be related to the integer terms? Let's explore different scenarios:
-
Scenario 1: 'n' as a constant: If 'n' were a constant value, we would expect to see a repeating pattern or a discernible relationship once 'n' is substituted. However, trying various constant values for 'n' doesn't reveal a consistent pattern within the sequence.
-
Scenario 2: 'n' as a function of position: It's possible that the value of 'n' depends on its position within the sequence. This implies a more intricate function that maps the sequence position to the value of 'n'. This requires more data points to establish a credible function. With only two 'n' terms, determining such a function is currently impossible.
-
Scenario 3: 'n' as an iterative function: Another possibility is that 'n' is an iterative function, where the value of 'n' in one term influences the value of 'n' in subsequent terms. Again, more data is needed to accurately model this.
2. Considering the Sequence as Modular Arithmetic or a Cryptographic Cipher
Another approach is to consider the possibility of modular arithmetic or a cryptographic cipher being involved. Modular arithmetic involves operations on integers where the result is the remainder after division by a specific number (the modulus). Could the sequence represent remainders after division by a particular modulus?
Let's examine the sequence modulo different numbers:
- Modulo 3: 4 mod 3 = 1, 7 mod 3 = 1, 2 mod 3 = 2. This doesn't show a clear pattern.
- Modulo 4: 4 mod 4 = 0, 7 mod 4 = 3, 2 mod 4 = 2. This also lacks a clear pattern.
- Modulo 5: 4 mod 5 = 4, 7 mod 5 = 2, 2 mod 5 = 2. Again, no discernible pattern.
Trying various moduli doesn't reveal a consistent modular arithmetic relationship. Similarly, if this were a simple substitution cipher, we lack sufficient information to decipher it. More terms in the sequence would be necessary to identify any such pattern.
3. Exploring the Sequence as a Piece of a Larger Pattern or Puzzle
It's possible that the sequence is only a fragment of a larger, more complex pattern. The incompleteness of the sequence hinders our ability to identify any intricate relationships. Additional terms could potentially unlock the hidden structure.
Let's hypothesize scenarios where the provided sequence is part of a broader mathematical or logical context:
-
Scenario 1: Recursive Sequence: The sequence might follow a recursive rule where each term is generated from previous terms. However, the lack of a clear recursive pattern from the given sequence prevents its determination.
-
Scenario 2: Fibonacci-like Sequence: The sequence might be a variation of a Fibonacci sequence, where each term is the sum of the two preceding terms. However, this doesn't fit the given pattern.
-
Scenario 3: Fractals or Chaotic Systems: In some cases, seemingly random sequences can arise from underlying fractal or chaotic systems. The current data is insufficient to explore this possibility.
4. The Importance of Context and Additional Information
The critical limitation in deciphering the sequence is the lack of context and additional data. Without further information, identifying the underlying pattern is speculative. The presence of 'n' significantly increases the complexity, potentially hinting at an algebraic or programmatic generation mechanism.
To effectively analyze this sequence, we would need to consider the following:
- Source of the Sequence: Where did this sequence originate? Knowing the source could provide crucial clues about its nature. Was it from a mathematical puzzle, a programming challenge, or a scientific experiment?
- Additional Terms: More terms in the sequence would greatly improve the chances of identifying a pattern. Additional data points would help rule out certain possibilities and refine our understanding of potential relationships.
- Underlying Constraints or Rules: Are there any implicit rules or constraints governing the sequence's generation? Knowing the rules could significantly simplify the analysis.
5. Applying Advanced Techniques
For more complex patterns, advanced techniques might be necessary:
- Statistical Analysis: Statistical methods like autocorrelation or spectral analysis could reveal hidden patterns within the sequence.
- Machine Learning: Machine learning algorithms, particularly those designed for time series analysis, could potentially identify patterns too intricate for human observation.
- Symbolic Regression: This technique aims to find mathematical equations that best fit the given data, potentially uncovering a functional relationship generating the sequence.
Conclusion: The Enigma Remains
The sequence 4, 5n, 7, 10n, 2 presents a fascinating challenge in pattern recognition and mathematical logic. While we have explored several approaches to deciphering its structure, the limited data prevents a definitive conclusion. The presence of the variable 'n' introduces a significant layer of complexity, highlighting the need for more information or context. However, the exploration itself underscores the power of systematic analysis, logical reasoning, and the importance of considering multiple mathematical perspectives when faced with an apparently random sequence. The journey towards understanding this enigmatic sequence serves as a valuable exercise in problem-solving and the development of critical thinking skills, demonstrating the often subtle yet intricate beauty of mathematics. Further investigation, with additional data points and context, is necessary to fully unravel the mystery of this intriguing numerical arrangement.
Latest Posts
Latest Posts
-
Financial Algebra Workbook Answer Key
Sep 23, 2025
-
How Many Pounds Is 24oz
Sep 23, 2025
-
Convert 28 Cm To Inches
Sep 23, 2025
-
Meaning Of Root Word Spect
Sep 23, 2025
-
Pcl5 Is Polar Or Nonpolar
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 4 5n 7 10n 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.