4 Times What Equals 28
gasmanvison
Sep 20, 2025 · 5 min read
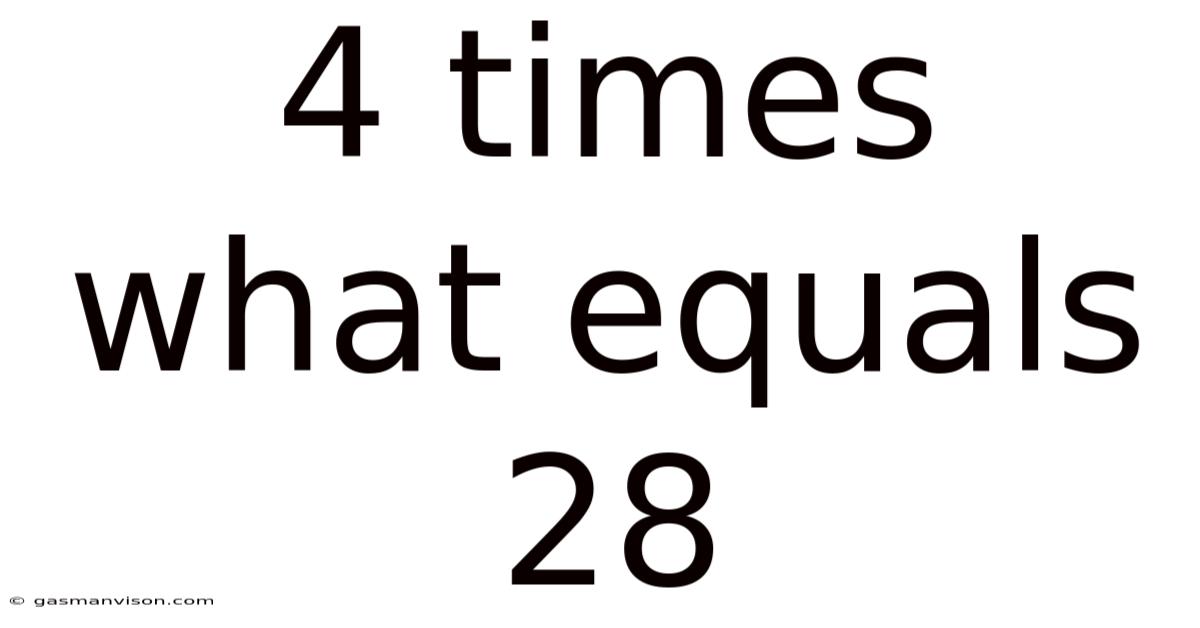
Table of Contents
4 Times What Equals 28? Unpacking a Simple Equation and its Broader Mathematical Implications
This seemingly simple question, "4 times what equals 28?", opens the door to a fascinating exploration of fundamental mathematical concepts and their applications in various fields. While the immediate answer is readily apparent, delving deeper reveals the underlying principles of algebra, the importance of problem-solving strategies, and the connections to more complex mathematical operations. This article will not only provide the answer but also explore the broader context and significance of this equation.
Meta Description: This article solves the equation "4 times what equals 28?" and explores its implications, covering algebraic solutions, problem-solving techniques, real-world applications, and connections to more advanced mathematical concepts. Learn how to approach similar problems and grasp the fundamental principles involved.
Finding the Solution: The Basics of Multiplication and Division
At its core, "4 times what equals 28?" is a simple multiplication problem. We can represent it algebraically as:
4 * x = 28
Where 'x' represents the unknown value we are trying to find. To solve for 'x', we employ the inverse operation of multiplication – division. Dividing both sides of the equation by 4 gives us:
x = 28 / 4
Therefore, x = 7. The answer is 7. Four times seven equals 28. This is a fundamental operation taught in elementary school, forming the bedrock of more advanced mathematical concepts.
Understanding the Problem-Solving Process: More Than Just Numbers
Solving "4 times what equals 28?" is not merely about arriving at the numerical answer; it's about understanding the problem-solving process itself. This process involves several key steps:
-
Understanding the Problem: Clearly identifying what the question is asking. In this case, it's identifying the number that, when multiplied by 4, results in 28.
-
Identifying the Relevant Information: Pinpointing the key numbers provided (4 and 28) and understanding their relationship.
-
Choosing an Appropriate Strategy: Selecting the correct mathematical operation (division) to solve the problem.
-
Performing the Calculation: Accurately carrying out the division operation (28 divided by 4).
-
Verifying the Solution: Checking the answer by performing the original multiplication (4 * 7 = 28). This step is crucial to ensure the accuracy of the solution.
Applications in Real-World Scenarios: From Shopping to Science
This seemingly simple equation has far-reaching applications in various aspects of daily life. Consider these examples:
-
Shopping: If four identical items cost $28, how much does one item cost? The equation directly applies, allowing you to calculate the price per item.
-
Baking: A recipe calls for 4 cups of flour to make 28 cookies. How much flour is needed per cookie? This is a direct application of the same principle.
-
Distribution: If 28 toys need to be divided equally among 4 children, how many toys will each child receive? Again, the division inherent in solving the equation provides the answer.
-
Science: Many scientific calculations involve ratios and proportions, often expressed in the form of simple equations like this one. For instance, determining the concentration of a solution or calculating the speed of an object based on distance and time.
These are just a few examples; the application of this simple equation extends to a surprisingly wide range of scenarios, highlighting the power of basic mathematical skills.
Expanding the Concept: Algebra and Equations
The equation "4 times what equals 28?" serves as an excellent introduction to the broader field of algebra. Algebra involves using symbols (like 'x') to represent unknown quantities and manipulating equations to solve for those unknowns. This equation exemplifies the basic principles of algebraic manipulation. We can further complicate this simple equation to illustrate more complex algebraic principles:
For instance, consider the equation: 4x + 6 = 34
This equation introduces an additional step. Before we can solve for 'x', we must first isolate the term containing 'x' by subtracting 6 from both sides:
4x = 28
This brings us back to our original equation, which we already know how to solve:
x = 7
This demonstrates how more complex algebraic equations can be simplified to fundamental equations like the one we initially explored.
Exploring Related Concepts: Factors, Multiples, and Divisibility
Understanding "4 times what equals 28?" also necessitates exploring the related concepts of factors, multiples, and divisibility.
-
Factors: The factors of 28 are the numbers that divide evenly into 28. These include 1, 2, 4, 7, 14, and 28. 4 is a factor of 28.
-
Multiples: The multiples of 4 are the numbers obtained by multiplying 4 by integers (whole numbers). These include 4, 8, 12, 16, 20, 24, 28, and so on. 28 is a multiple of 4.
-
Divisibility: 28 is divisible by 4 because it can be divided evenly by 4 without leaving a remainder.
Understanding these concepts provides a deeper understanding of the numerical relationships involved in the equation.
Beyond the Basics: Extending the Problem
We can extend the initial problem in several ways to reinforce understanding and challenge mathematical skills:
-
Using larger numbers: "12 times what equals 144?" This problem uses larger numbers but still follows the same basic principles.
-
Introducing fractions: "4 times what equals 21?" This problem introduces fractions and requires a slightly more complex calculation. The answer would be 21/4 or 5 1/4.
-
Adding multiple variables: "4x + 2y = 28" This equation introduces a second variable and requires additional information or another equation to solve for both x and y.
These variations help to build problem-solving skills and solidify understanding of the underlying mathematical concepts.
The Importance of Practice and Exploration
Mastering mathematical skills, like solving equations, requires consistent practice and exploration. Working through various problems, starting with simple equations and gradually increasing complexity, builds confidence and proficiency. This continuous learning process is essential for applying mathematical knowledge effectively in various contexts.
Conclusion: A Foundation for Future Learning
The seemingly simple question, "4 times what equals 28?", serves as a powerful starting point for understanding fundamental mathematical concepts. It highlights the importance of problem-solving strategies, showcases applications in various fields, and forms a cornerstone for exploring more complex algebraic concepts and numerical relationships. By understanding this simple equation and the principles behind its solution, one builds a strong foundation for future mathematical learning and problem-solving endeavors. This exploration extends beyond simply finding the answer of 7, delving into the world of mathematics and its multifaceted applications in everyday life and beyond.
Latest Posts
Latest Posts
-
Designing For Recycling Helps Facilitate
Sep 20, 2025
-
Religion In Schools Political Cartoon
Sep 20, 2025
-
Is 30 3 An Integer
Sep 20, 2025
-
Is 16 Ounces A Pound
Sep 20, 2025
-
How Many Grams Half Pound
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 4 Times What Equals 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.