4 X 3 4x 12
gasmanvison
Sep 22, 2025 · 5 min read
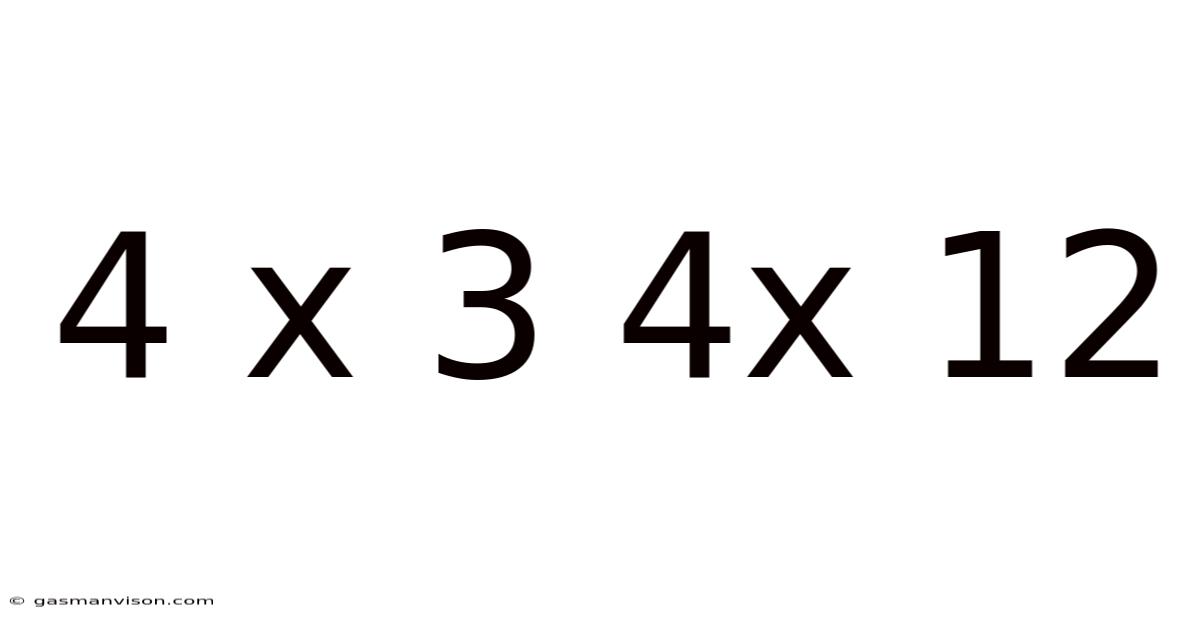
Table of Contents
Deconstructing the Enigma: Exploring the Mathematical and Practical Implications of "4 x 3" and "4 x 12"
This article delves into the seemingly simple mathematical expressions "4 x 3" and "4 x 12," exploring their fundamental calculations, practical applications across various fields, and the underlying principles that govern their significance. While the calculations themselves are straightforward, their implications extend far beyond basic arithmetic, offering insights into scaling, proportionality, and the foundational building blocks of more complex mathematical concepts. Understanding these simple multiplications lays the groundwork for comprehending more advanced topics like algebra, geometry, and even calculus.
Understanding the Basics: Multiplication as Repeated Addition
At their core, "4 x 3" and "4 x 12" represent multiplication problems. Multiplication can be understood as repeated addition. "4 x 3" signifies adding four to itself three times (4 + 4 + 4 = 12), resulting in a product of 12. Similarly, "4 x 12" means adding four to itself twelve times (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 48), yielding a product of 48. This fundamental understanding is crucial, especially when teaching these concepts to younger learners. Visual aids like blocks or counters can effectively demonstrate this repeated addition process, making the concept more concrete and intuitive.
Practical Applications: From Everyday Life to Advanced Sciences
The applications of these seemingly simple multiplications are vast and far-reaching, permeating various aspects of our lives:
Everyday Scenarios:
- Shopping: Calculating the total cost of four items priced at $3 each (4 x $3 = $12) or twelve items priced at $4 each (4 x $12 = $48). This is a fundamental skill used daily by consumers.
- Cooking & Baking: Doubling or tripling recipes often involves multiplying ingredient quantities. If a recipe calls for 3 cups of flour, and you want to make four times the amount, you'll need 4 x 3 = 12 cups of flour.
- Construction & Design: Calculating the number of bricks needed for a wall or the area of a floor often involves multiplying dimensions. If you need four rows of bricks, each containing 12 bricks, you’ll need 4 x 12 = 48 bricks.
- Time Management: Calculating the total time spent on an activity. Four 3-hour work sessions total 4 x 3 = 12 hours of work.
Advanced Applications:
- Engineering & Physics: Scaling designs and calculating forces often involve multiplying factors. Consider the stress on a structure: understanding the multiplication of force and area is crucial for structural integrity.
- Computer Science: Array processing and loop iterations frequently utilize multiplication to determine the number of operations required. A nested loop might involve multiplying the number of iterations in each loop to determine the total number of computations.
- Finance & Accounting: Calculating interest earned or taxes owed often involves multiplication. For instance, calculating compound interest uses exponential growth which relies on repeated multiplication.
- Data Analysis & Statistics: Calculating frequencies, proportions, and probabilities often relies on multiplication. Statistical analysis frequently involves working with large datasets requiring efficient multiplication techniques.
Expanding the Scope: Exploring Related Concepts
The simple multiplication problems "4 x 3" and "4 x 12" are stepping stones to more complex mathematical concepts:
Factors and Multiples:
- Factors: The numbers 4 and 3 are factors of 12, meaning they divide evenly into 12 without leaving a remainder. Similarly, 4 and 12 are factors of 48. Understanding factors is crucial in factorization, a cornerstone of algebra.
- Multiples: 12 is a multiple of 4 and 3, and 48 is a multiple of 4 and 12. This concept helps in understanding number patterns and divisibility rules.
Distributive Property:
The distributive property states that a(b + c) = ab + ac. This property allows us to break down complex multiplication problems into simpler ones. For example, we can calculate 4 x 15 as 4 x (10 + 5) = (4 x 10) + (4 x 5) = 40 + 20 = 60. This simplification is incredibly useful in more advanced algebra.
Commutative Property:
The commutative property of multiplication states that a x b = b x a. This means that the order of numbers in a multiplication problem does not affect the result. Therefore, 4 x 3 is the same as 3 x 4, and 4 x 12 is the same as 12 x 4. This seemingly simple property has profound implications in simplifying calculations and understanding mathematical structures.
Associative Property:
The associative property states that (a x b) x c = a x (b x c). This means that the grouping of numbers in a multiplication problem does not affect the result. This property becomes particularly useful when dealing with more than two numbers. For example, (4 x 3) x 2 = 4 x (3 x 2) = 24.
Beyond the Numbers: Developing Mathematical Thinking
The importance of understanding "4 x 3" and "4 x 12" extends beyond mere calculation. These simple problems lay the foundation for developing crucial mathematical thinking skills:
- Problem-solving: Applying these multiplications to real-world scenarios hones problem-solving abilities.
- Pattern recognition: Observing patterns in multiples and factors helps in developing number sense and algebraic thinking.
- Critical thinking: Analyzing the implications and applications of these multiplications promotes critical thinking skills.
- Abstract thinking: Moving beyond concrete examples to understand the underlying principles cultivates abstract thinking.
Conclusion: The Enduring Significance of Simple Arithmetic
While "4 x 3 = 12" and "4 x 12 = 48" may appear trivial at first glance, their significance is profound. These seemingly simple multiplications are the building blocks of more complex mathematical concepts, and their applications are widespread, touching almost every facet of our lives, from daily routines to advanced scientific endeavors. A deep understanding of these fundamental operations is essential for developing strong mathematical skills and fostering critical thinking abilities. Mastering these basics empowers individuals to navigate the complexities of the world around them with confidence and competence, showcasing the lasting impact of seemingly simple arithmetic. The seemingly simple equations unlock a universe of understanding and problem-solving capabilities, highlighting the crucial role of foundational mathematics in shaping our world.
Latest Posts
Latest Posts
-
Electron Dot Notation For Nitrogen
Sep 22, 2025
-
6 5 Percent As A Decimal
Sep 22, 2025
-
What Is 2 52 Of 25
Sep 22, 2025
-
What Is A Multimedia Presentation
Sep 22, 2025
-
A Farmhouse Shelters 10 Animals
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 4x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.