41 Of 78 Is What
gasmanvison
Sep 23, 2025 · 5 min read
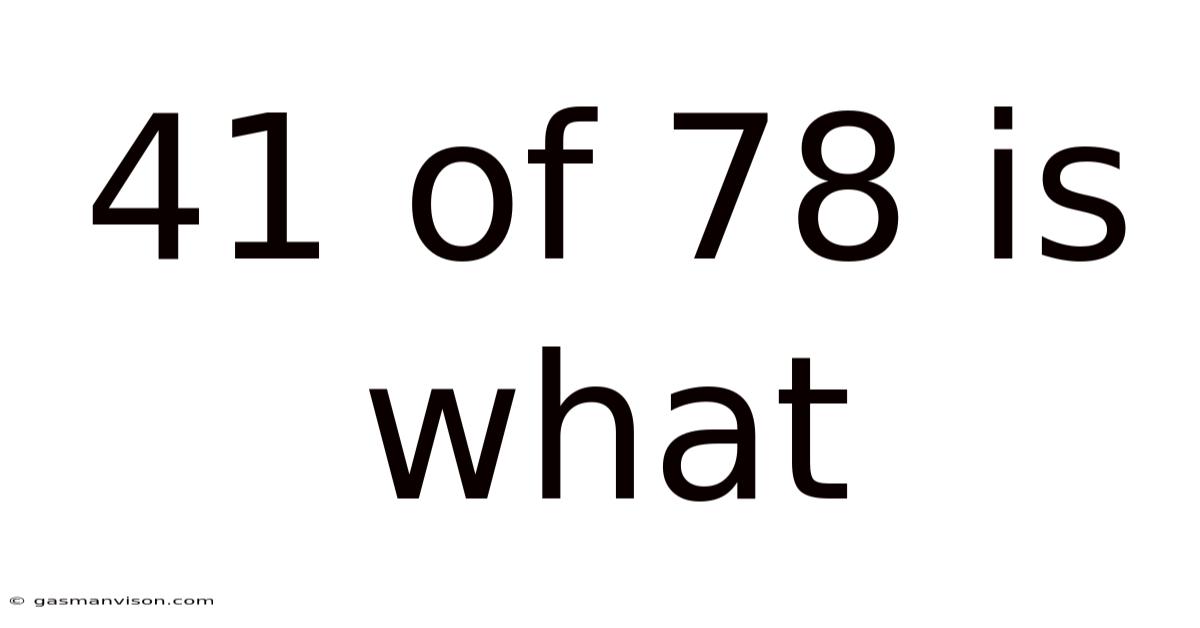
Table of Contents
Decoding Percentages: A Deep Dive into "41 out of 78 is What?"
Meta Description: Uncover the intricacies of percentage calculations. This comprehensive guide explains how to determine what percentage 41 out of 78 represents, covering various methods, real-world applications, and advanced percentage concepts. Learn to confidently tackle percentage problems in any context.
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. Whether you're calculating discounts, grading exams, or analyzing survey results, mastering percentage calculations is crucial. This in-depth article will not only solve the specific problem of "41 out of 78 is what?" but also provide you with a comprehensive understanding of percentages and related calculations.
We'll explore multiple methods to arrive at the answer, discuss the underlying concepts, and offer practical examples to solidify your understanding. By the end, you'll be able to confidently tackle similar percentage problems and apply your knowledge to various situations.
Method 1: The Basic Percentage Formula
The most straightforward approach to solving "41 out of 78 is what?" involves using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 41 (the number we're considering as a portion of the whole)
- Whole: 78 (the total number)
Substituting these values into the formula:
(41 / 78) x 100% = 52.56% (approximately)
Therefore, 41 out of 78 is approximately 52.56%.
Method 2: Using Decimal Equivalents
Another approach involves converting the fraction (41/78) into a decimal first, then multiplying by 100% to obtain the percentage.
-
Divide the part by the whole: 41 ÷ 78 ≈ 0.5256
-
Multiply the decimal by 100%: 0.5256 x 100% = 52.56%
This method offers a slightly different perspective on the calculation, reinforcing the core concept of representing a portion as a fraction of the whole.
Method 3: Proportion Method
This method leverages the concept of proportion, setting up an equation to solve for the unknown percentage.
Let 'x' represent the percentage we're trying to find. We can set up the proportion:
41/78 = x/100
To solve for x, cross-multiply:
78x = 4100
Now, divide both sides by 78:
x = 4100 / 78 ≈ 52.56
Therefore, x ≈ 52.56%, confirming our previous results.
Understanding the Result: 52.56%
The result, 52.56%, signifies that 41 represents approximately 52.56% of 78. This percentage can be interpreted in various contexts. For example, if 78 represents the total number of students in a class and 41 students passed an exam, then the pass rate is approximately 52.56%.
Rounding and Precision
Notice that our result includes decimal places. The level of precision required depends on the context. In some cases, rounding to a whole number (53%) might suffice, while in others, maintaining more decimal places is necessary for accuracy. Always consider the context to determine the appropriate level of rounding.
Practical Applications of Percentage Calculations
Percentage calculations are incredibly versatile and have numerous practical applications. Here are a few examples:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Statistics: Analyzing survey data, interpreting probability, and understanding population demographics.
- Retail: Determining sale prices, calculating markups, and analyzing sales trends.
- Education: Calculating grades, assessing student performance, and tracking academic progress.
- Science: Expressing experimental results, analyzing data, and understanding proportions.
- Everyday Life: Calculating tips, splitting bills, understanding discounts, and making comparisons.
Beyond the Basics: Advanced Percentage Concepts
While the "41 out of 78 is what?" problem provides a foundation in percentage calculation, let's delve into more advanced concepts:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a price increased from $50 to $60, the percentage increase is [(60-50)/50] x 100% = 20%.
-
Percentage Points: This concept is often confused with percentage change. Percentage points refer to the absolute difference between two percentages. For instance, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points, not 60%.
-
Compound Interest: This involves earning interest on both the principal amount and accumulated interest. It's a crucial concept in finance and investment.
-
Percentage of a Percentage: Calculating a percentage of a previously calculated percentage. For example, finding 10% of a 25% discount.
-
Working Backwards from a Percentage: Determining the original value when given a percentage and the resulting value.
Improving Your Percentage Calculation Skills
Here are some tips to improve your proficiency in percentage calculations:
-
Practice Regularly: Solve various percentage problems to build your confidence and understanding.
-
Use Different Methods: Experiment with different approaches (formula, decimals, proportion) to find the method you find most intuitive.
-
Understand the Context: Always consider the real-world application of the percentage calculation to ensure you're interpreting the results correctly.
-
Utilize Online Resources: Numerous online calculators and tutorials can assist you in learning and practicing percentage calculations.
-
Seek Help When Needed: Don't hesitate to seek clarification or assistance if you're struggling with any aspect of percentage calculations.
Conclusion: Mastering the World of Percentages
Understanding percentages is a valuable skill applicable in various aspects of life. By mastering the fundamental formula and exploring advanced concepts, you'll equip yourself with a powerful tool for analyzing data, making informed decisions, and confidently tackling numerical problems. The solution to "41 out of 78 is what?" – approximately 52.56% – serves as a springboard to a deeper understanding of the broader world of percentages and their practical applications. Remember to practice regularly, and you'll soon find yourself comfortable and confident in tackling any percentage-related challenge.
Latest Posts
Latest Posts
-
Pcl5 Is Polar Or Nonpolar
Sep 23, 2025
-
The Story An Hour Summary
Sep 23, 2025
-
Which Item Should Be Rejected
Sep 23, 2025
-
How Many Pounds Is 48oz
Sep 23, 2025
-
183 Cm To Ft In
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 41 Of 78 Is What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.