4x 3y - 4y 10x
gasmanvison
Sep 15, 2025 · 5 min read
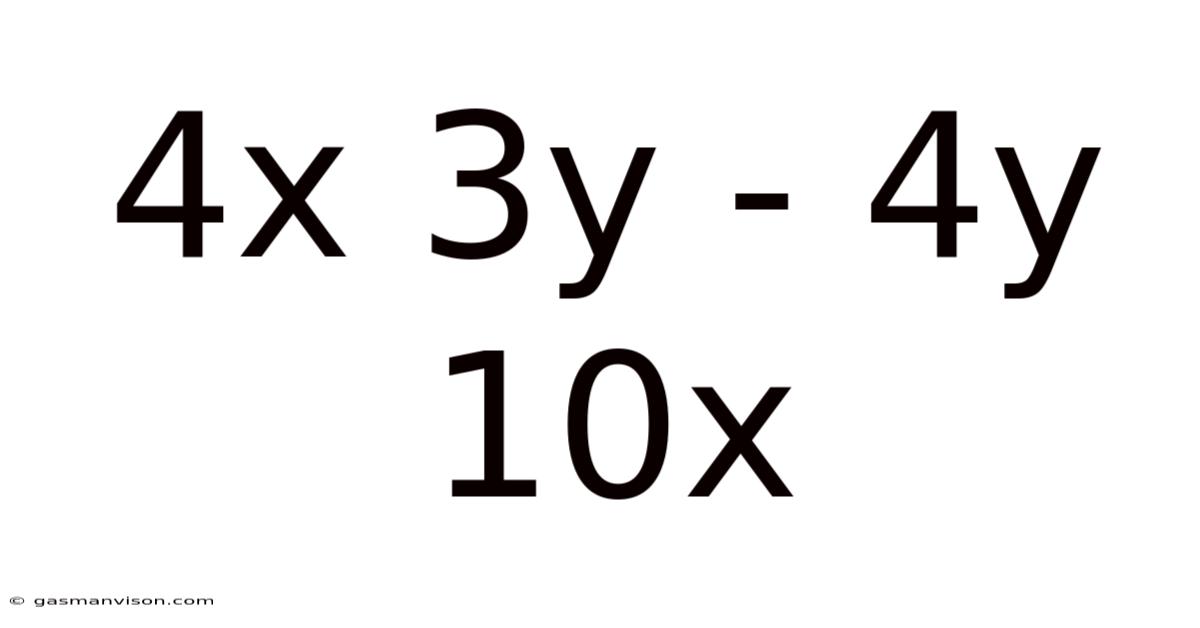
Table of Contents
Unraveling the Algebraic Expression: 4x + 3y - 4y + 10x
This article delves into the seemingly simple algebraic expression, 4x + 3y - 4y + 10x, exploring its simplification, applications, and the broader mathematical concepts it embodies. While the expression itself might appear basic, understanding its manipulation lays a crucial foundation for more complex algebraic operations and problem-solving. We'll cover simplification techniques, discuss its representation in different contexts, and explore how such expressions are used in real-world applications.
Meta Description: Learn how to simplify the algebraic expression 4x + 3y - 4y + 10x. This comprehensive guide covers simplification techniques, practical applications, and related mathematical concepts, perfect for students and anyone looking to improve their algebra skills.
Understanding the Components: Variables and Coefficients
Before embarking on the simplification process, let's define the key elements within the expression: 4x + 3y - 4y + 10x.
-
Variables: 'x' and 'y' are variables. Variables represent unknown quantities or values that can change. In this context, 'x' and 'y' are distinct variables, meaning they can hold independent values.
-
Coefficients: The numbers preceding the variables are coefficients. They represent the multiplicative factor of each variable. For instance, in '4x', '4' is the coefficient of 'x', indicating that 'x' is multiplied by 4. Similarly, '3' is the coefficient of 'y' in '3y', and '10' is the coefficient of 'x' in '10x'.
-
Constants: While not present in this specific expression, a constant is a numerical value that doesn't change. For example, in the expression 2x + 5, '5' is a constant.
Simplifying the Expression: Combining Like Terms
The core principle in simplifying algebraic expressions is combining like terms. Like terms are terms that have the same variables raised to the same powers. In our expression, 4x + 3y - 4y + 10x, we have two sets of like terms:
- Terms with 'x': 4x and 10x
- Terms with 'y': 3y and -4y
To simplify, we combine these like terms by adding or subtracting their coefficients:
-
Combining 'x' terms: 4x + 10x = 14x (We add the coefficients: 4 + 10 = 14)
-
Combining 'y' terms: 3y - 4y = -y (We subtract the coefficients: 3 - 4 = -1. We usually omit the '1' when the coefficient is -1)
Therefore, the simplified expression is 14x - y.
Visualizing the Simplification: A Geometric Approach
While algebraic manipulation is essential, visualizing the simplification can enhance understanding. Imagine 'x' and 'y' representing lengths or quantities. The expression 4x + 3y - 4y + 10x can be thought of as a series of lengths being added and subtracted. Combining like terms is akin to grouping these lengths together to find a total length. This geometric representation can be particularly helpful for beginners to grasp the concept of combining like terms.
Applications in Real-World Scenarios
Algebraic expressions like 4x + 3y - 4y + 10x are foundational to numerous real-world applications across diverse fields:
-
Physics: In physics, equations often involve variables representing quantities like distance, velocity, and time. Simplifying expressions is crucial for solving for unknown variables and predicting outcomes. For example, consider calculating the net displacement of an object moving in two dimensions where x and y represent displacements along the x and y axes.
-
Engineering: Engineers frequently use algebraic expressions to model systems and solve for optimal designs. Structural engineers might use them to calculate forces on beams, while electrical engineers might use them in circuit analysis.
-
Economics: Economic models often use variables to represent quantities like supply, demand, and profit. Simplifying algebraic expressions is essential for analyzing market behavior and making economic predictions.
-
Computer Science: In computer programming, algebraic expressions are fundamental to algorithm design and data manipulation. Optimizing these expressions can significantly impact program efficiency.
-
Finance: Financial modeling relies heavily on algebraic expressions to project investment returns, calculate loan repayments, and analyze risk.
Expanding the Concept: More Complex Expressions
While our example was relatively simple, the principles of combining like terms extend to far more complex algebraic expressions. Consider the expression:
2x² + 3xy - 5x + 4y² - 2xy + 7x
Here, we have several like terms:
- x² terms: 2x² (only one term)
- xy terms: 3xy and -2xy
- x terms: -5x and 7x
- y² terms: 4y² (only one term)
Simplifying this expression involves combining these like terms:
- 2x² remains unchanged.
- 3xy - 2xy = xy
- -5x + 7x = 2x
- 4y² remains unchanged
Therefore, the simplified expression becomes: 2x² + xy + 2x + 4y²
Working with Parentheses and Distributive Property
Introducing parentheses adds another layer of complexity but remains manageable using the distributive property. The distributive property states that a(b + c) = ab + ac. Consider the expression:
3(2x + y) - 4x + 2(x - 3y)
First, we apply the distributive property to remove the parentheses:
- 3(2x + y) = 6x + 3y
- 2(x - 3y) = 2x - 6y
Now, we substitute these back into the original expression:
6x + 3y - 4x + 2x - 6y
Finally, we combine like terms:
- x terms: 6x - 4x + 2x = 4x
- y terms: 3y - 6y = -3y
Thus, the simplified expression is: 4x - 3y
Advanced Applications: Systems of Equations
Algebraic expressions form the basis of solving systems of equations. A system of equations involves multiple equations with multiple variables. For example:
- 2x + y = 7
- x - 3y = -2
Solving these equations simultaneously can yield the values of 'x' and 'y'. Methods like substitution or elimination can be employed to find these values. The ability to simplify algebraic expressions within these equations is crucial for efficient and accurate solutions.
Conclusion: Mastering the Fundamentals
The seemingly simple algebraic expression, 4x + 3y - 4y + 10x, serves as a gateway to understanding fundamental algebraic principles. Mastering the simplification of such expressions, through the process of combining like terms, lays a strong foundation for tackling more complex mathematical problems across various disciplines. The ability to manipulate and simplify algebraic expressions is not merely an academic exercise; it's a crucial skill with far-reaching practical applications in diverse fields, from engineering and physics to economics and computer science. By thoroughly understanding these foundational concepts, individuals can build a solid mathematical base for future learning and problem-solving endeavors. Understanding the simplification of expressions like 4x + 3y - 4y + 10x empowers individuals to confidently tackle more complex algebraic challenges and apply their mathematical skills to a wide range of real-world situations.
Latest Posts
Latest Posts
-
Density Of Water Kg L
Sep 15, 2025
-
210 Degrees Celsius To Fahrenheit
Sep 15, 2025
-
Greg Tossed A Number Cube
Sep 15, 2025
-
How To Find Frequency Stats
Sep 15, 2025
-
Ounces In 750 Ml Bottle
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 4x 3y - 4y 10x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.