5 3/4 In Decimal Form
gasmanvison
Sep 13, 2025 · 5 min read
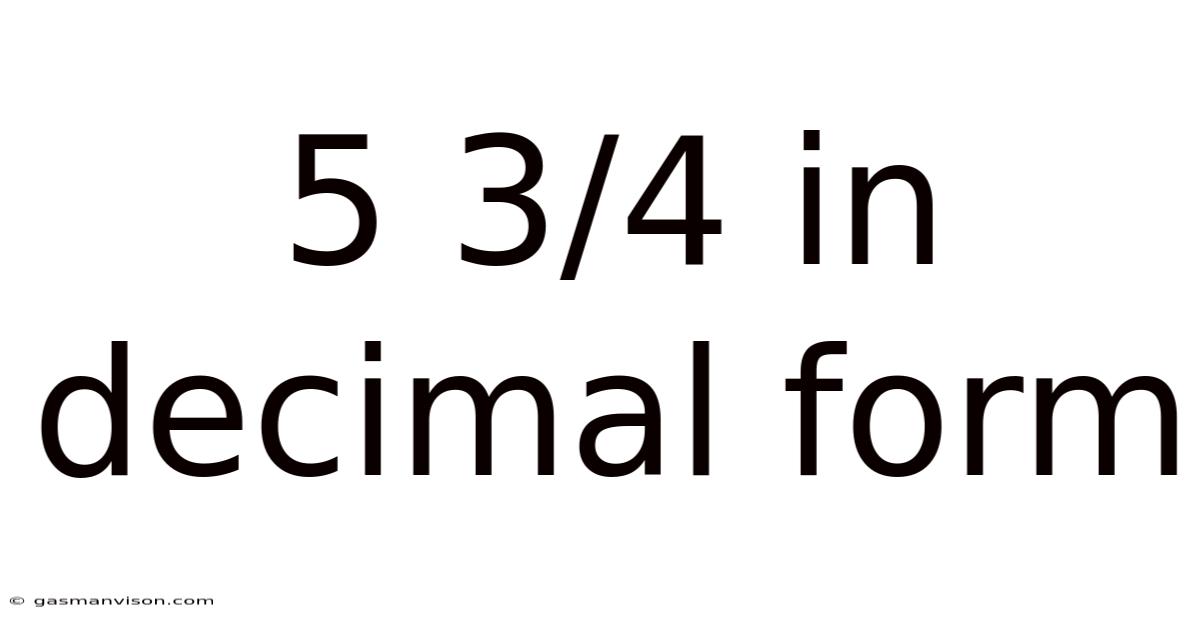
Table of Contents
5 3/4 in Decimal Form: A Comprehensive Guide
Meta Description: Learn how to convert the mixed number 5 3/4 into its decimal equivalent. This comprehensive guide explores the conversion process step-by-step, offers alternative methods, and explores practical applications of understanding decimal conversions.
Converting fractions to decimals is a fundamental skill in mathematics with broad applications in various fields, from everyday calculations to advanced scientific computations. This article focuses specifically on converting the mixed number 5 3/4 into its decimal form. We'll delve into the process, explore different approaches, and discuss why understanding this conversion is crucial.
Understanding Mixed Numbers and Decimals
Before we begin the conversion, let's briefly refresh our understanding of mixed numbers and decimals.
-
Mixed Numbers: A mixed number combines a whole number and a fraction. In our case, 5 3/4 represents 5 whole units and 3/4 of another unit.
-
Decimals: Decimals represent fractions where the denominator is a power of 10 (10, 100, 1000, etc.). They are expressed using a decimal point to separate the whole number part from the fractional part. For example, 0.5 represents 5/10, and 0.75 represents 75/100.
Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number
This is the most straightforward method. We first convert the fractional part (3/4) into a decimal and then add the whole number (5).
Step 1: Convert the Fraction to a Decimal
To convert 3/4 to a decimal, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Step 2: Add the Whole Number
Now, we add the whole number part (5) to the decimal equivalent of the fraction (0.75):
5 + 0.75 = 5.75
Therefore, 5 3/4 in decimal form is 5.75.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed number into an improper fraction and then dividing the numerator by the denominator.
Step 1: Convert to an Improper Fraction
To convert 5 3/4 to an improper fraction, we multiply the whole number (5) by the denominator (4) and add the numerator (3). The result becomes the new numerator, while the denominator remains the same:
(5 * 4) + 3 = 23
So, 5 3/4 becomes 23/4.
Step 2: Convert the Improper Fraction to a Decimal
Now, we divide the numerator (23) by the denominator (4):
23 ÷ 4 = 5.75
Again, we arrive at the decimal equivalent of 5.75.
Method 3: Using Decimal Equivalents of Common Fractions
This method relies on memorizing the decimal equivalents of common fractions. Knowing that 1/4 = 0.25, we can quickly deduce that 3/4 = 3 * 0.25 = 0.75. Adding the whole number 5 gives us 5.75. This method is efficient for commonly used fractions but requires prior knowledge of these equivalents.
Why is Understanding Decimal Conversions Important?
The ability to convert fractions to decimals is crucial for several reasons:
-
Simplified Calculations: Decimals are generally easier to work with in calculations, especially when using calculators or computers. Adding, subtracting, multiplying, and dividing decimals is often more straightforward than performing the same operations with fractions.
-
Real-World Applications: Many real-world measurements and quantities are expressed using decimals. For example, money, weights, lengths, and volumes are frequently represented using decimal notation. Understanding decimal conversions allows for seamless integration of fractional values into these real-world applications.
-
Data Analysis and Interpretation: In fields like statistics, finance, and science, data is often presented using decimals. The ability to convert fractions to decimals is necessary to analyze and interpret this data effectively.
-
Problem Solving: Many mathematical problems involve both fractions and decimals. Converting between these forms is essential to solve these problems efficiently and accurately.
-
Software and Programming: Most computer programs and software applications work primarily with decimal numbers. Converting fractions to decimals is essential for programming calculations and data manipulation.
Practical Examples Using 5.75
Let's illustrate the practical application of the decimal equivalent 5.75 with a few examples:
-
Finance: If you have 5 ¾ dollars, that’s equal to $5.75. This is easily understood and used in financial transactions.
-
Measurement: Imagine measuring a length. If a piece of wood measures 5 ¾ inches, you can readily use the decimal equivalent 5.75 inches in your calculations.
-
Baking: Recipes often use fractional measurements. If a recipe calls for 5 ¾ cups of flour, knowing that this equals 5.75 cups makes measuring and following the recipe much simpler, especially when using digital kitchen scales.
-
Scientific Calculations: In scientific settings, precise measurements are crucial. Converting fractions to decimals ensures accurate calculations and data representation.
Advanced Concepts and Further Exploration
While converting 5 3/4 to 5.75 is relatively straightforward, understanding the broader concepts behind decimal conversions allows for the application of these principles to more complex scenarios.
-
Converting recurring decimals: Some fractions, when converted to decimals, produce recurring decimals (e.g., 1/3 = 0.333...). Understanding how to represent and work with these recurring decimals is a valuable skill.
-
Converting decimals to fractions: This is the reverse process of what we've covered. Knowing how to convert decimals back into fractions is equally important for a complete understanding of the relationship between these two number representations.
-
Significant figures and rounding: When dealing with decimals resulting from measurements, understanding significant figures and rounding is crucial for maintaining accuracy and avoiding unnecessary precision.
Conclusion
Converting the mixed number 5 3/4 to its decimal equivalent, 5.75, is a simple yet fundamental mathematical operation. This seemingly basic conversion highlights the importance of understanding the relationship between fractions and decimals. The ability to seamlessly convert between these forms is not only essential for everyday calculations but also crucial for success in various academic and professional fields. By mastering this skill and exploring related concepts, you build a strong foundation for more advanced mathematical understanding and problem-solving. The ability to effortlessly translate between fractional and decimal representations unlocks a broader understanding of numerical concepts and their wide-ranging applications in the real world.
Latest Posts
Latest Posts
-
Use Implore In A Sentence
Sep 13, 2025
-
How Do You Spell 80
Sep 13, 2025
-
What Is 29cm In Inches
Sep 13, 2025
-
Stairs Should Be Installed Between
Sep 13, 2025
-
500 Ml In A Liter
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5 3/4 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.