5 Divided By 1 3
gasmanvison
Sep 24, 2025 · 6 min read
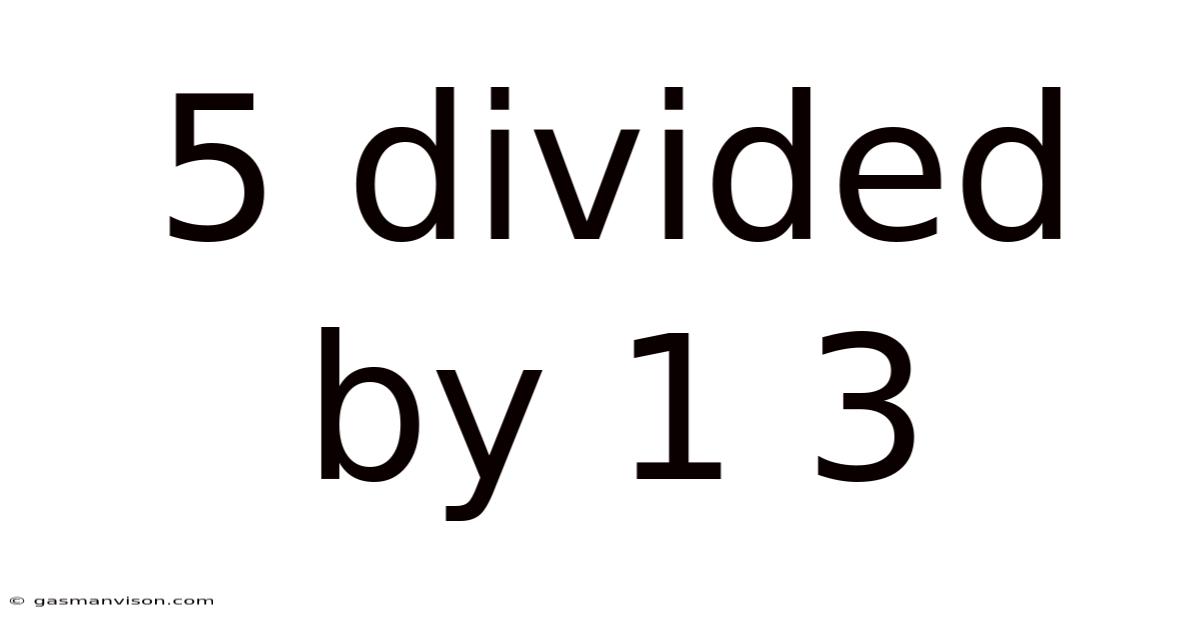
Table of Contents
Decoding 5 Divided by 1 3: A Deep Dive into Division and Fractions
Meta Description: This comprehensive guide explores the intricacies of dividing 5 by 1 3/5, covering various methods including converting mixed numbers to improper fractions, reciprocal multiplication, and practical applications. Learn how to solve this problem and similar division problems with fractions confidently.
Dividing 5 by 1 3/5 might seem like a simple arithmetic problem, but it touches upon fundamental concepts in mathematics crucial for understanding fractions, mixed numbers, and the process of division itself. This article will not only show you how to solve 5 ÷ 1 3/5, but also delve into the underlying principles, offering a deeper understanding of the methodology and its broader applications.
We’ll explore different approaches to tackling this problem, explaining each step in detail to ensure clarity. Whether you're a student brushing up on your math skills, a teacher looking for supplementary teaching materials, or simply someone curious about the intricacies of fractions, this guide will provide a comprehensive and insightful journey into the world of mathematical division.
Understanding the Components: Fractions and Mixed Numbers
Before diving into the division problem, let's revisit the essential components: fractions and mixed numbers.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator.
-
Mixed Numbers: A mixed number combines a whole number and a fraction. For instance, 1 3/5 represents one whole unit and three-fifths of another unit.
In our problem, 5 is a whole number, and 1 3/5 is a mixed number. Understanding how to manipulate these number types is key to solving the problem effectively.
Method 1: Converting to Improper Fractions
The most straightforward approach to solving 5 ÷ 1 3/5 is to convert both the whole number and the mixed number into improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator.
-
Converting 1 3/5 to an improper fraction: To do this, multiply the whole number (1) by the denominator (5) and add the numerator (3). This result (1*5 + 3 = 8) becomes the new numerator. The denominator remains the same (5). Therefore, 1 3/5 becomes 8/5.
-
Converting 5 to an improper fraction: Any whole number can be expressed as a fraction by placing it over 1. Thus, 5 becomes 5/1.
Now our problem becomes: 5/1 ÷ 8/5
Method 2: Reciprocal Multiplication
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of 8/5 is 5/8.
Therefore, our problem transforms into: 5/1 x 5/8
Method 3: Performing the Multiplication
Multiplying fractions involves multiplying the numerators together and the denominators together:
(5 x 5) / (1 x 8) = 25/8
Method 4: Converting Back to a Mixed Number (If Necessary)
The result 25/8 is an improper fraction. To convert it back to a mixed number, divide the numerator (25) by the denominator (8):
25 ÷ 8 = 3 with a remainder of 1.
This means that 25/8 is equal to 3 1/8.
Therefore, the solution to 5 ÷ 1 3/5 is 3 1/8.
Alternative Method: Long Division with Fractions
While the improper fraction method is generally preferred for its efficiency, understanding long division with fractions can offer a deeper insight into the process. This method involves breaking down the division into smaller, manageable steps.
-
Set up the problem: Write the problem as 5 ÷ 1 3/5.
-
Convert the mixed number to a decimal: Convert 1 3/5 to its decimal equivalent (1.6). This makes the problem 5 ÷ 1.6.
-
Perform long division: Use the standard long division method to divide 5 by 1.6. This will require adding a decimal point to 5 (making it 5.000) to allow for a more precise answer. The result will be approximately 3.125.
-
Convert the decimal to a fraction: Convert 3.125 back into a fraction. This involves recognising that 0.125 is equal to 1/8. Therefore, 3.125 becomes 3 1/8.
This demonstrates that the result using the long division method with decimals confirms the answer obtained using the improper fraction method: 3 1/8.
Practical Applications of Fraction Division
Understanding fraction division extends beyond the realm of theoretical mathematics. It finds practical applications in various real-world scenarios:
-
Recipe Scaling: If a recipe calls for 1 3/5 cups of flour and you want to make a batch five times larger, you would need to calculate 5 ÷ 1 3/5 to determine the total amount of flour required.
-
Measurement Conversions: Many measurement conversions involve fractions. For example, converting between different units of length or weight often requires dividing or multiplying by fractions.
-
Resource Allocation: In project management or resource allocation, dividing tasks or resources might involve fractions. For instance, if you have 5 hours to complete a project and one task requires 1 3/5 hours, you can determine how many times that task can be performed.
-
Data Analysis: Working with statistical data frequently involves dealing with fractions and performing divisions to calculate averages, proportions, or ratios.
-
Construction and Engineering: Blueprints and construction plans utilize fractions extensively. Calculating materials or proportions requires a deep understanding of fraction division.
Expanding on the Concepts: More Complex Problems
The principles discussed here can be applied to more complex fraction division problems. Consider a problem like: (2 1/2) ÷ (3 2/3).
-
Convert to improper fractions: 2 1/2 becomes 5/2 and 3 2/3 becomes 11/3.
-
Find the reciprocal and multiply: The problem becomes (5/2) x (3/11).
-
Multiply the numerators and denominators: This gives (5 x 3) / (2 x 11) = 15/22.
This demonstrates that the methods outlined for the simpler problem (5 ÷ 1 3/5) are equally applicable to more challenging fraction division scenarios.
Conclusion: Mastering Fraction Division
The seemingly simple problem of 5 divided by 1 3/5 provides a powerful illustration of the fundamental principles of fraction manipulation and division. By understanding the conversion between mixed numbers and improper fractions, the concept of reciprocals in division, and the application of standard multiplication and division techniques, you can confidently approach and solve a wide array of fraction division problems. These skills are invaluable not only for academic success but also for navigating numerous practical applications in daily life. Remember that consistent practice and a clear understanding of the underlying concepts are key to mastering this important mathematical skill.
Latest Posts
Latest Posts
-
What Is 20 Of 70
Sep 24, 2025
-
Convert 73 F To C
Sep 24, 2025
-
Rough Er Pick Up Lines
Sep 24, 2025
-
One Rhetorical Choice Jen Makes
Sep 24, 2025
-
1 8 Cup In Oz
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.