5 Square Root Of 3
gasmanvison
Sep 08, 2025 · 5 min read
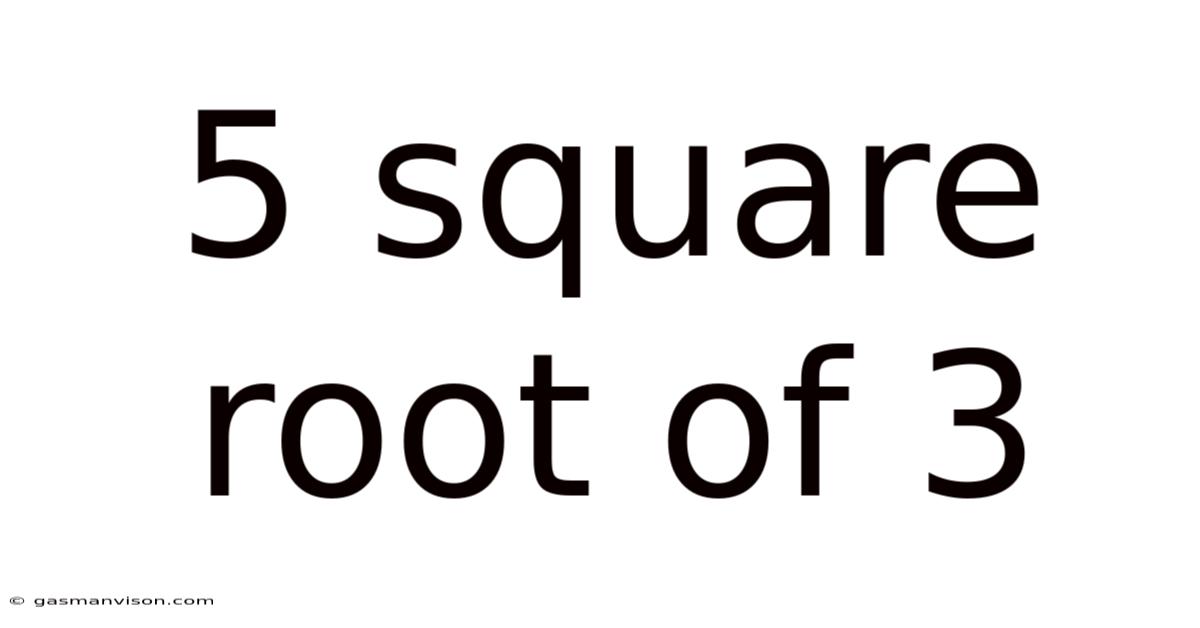
Table of Contents
Decoding 5√3: Exploring the Mathematical Concept and its Applications
This article delves deep into the mathematical expression 5√3, exploring its meaning, calculations, geometric interpretations, and practical applications across various fields. Understanding this seemingly simple expression unlocks a deeper appreciation for fundamental mathematical concepts and their relevance in the real world. We'll explore its properties, approximations, and how it appears in different contexts, from trigonometry to physics. This comprehensive guide aims to provide a clear and accessible explanation for both students and anyone curious about the mathematical intricacies of 5√3.
What is 5√3?
At its core, 5√3 represents the product of two numbers: 5 and the square root of 3 (√3). The square root of 3 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. Its approximate value is 1.732. Therefore, 5√3 is approximately 5 * 1.732 = 8.660. However, it's crucial to understand that 8.660 is just an approximation; the true value of 5√3 is infinitely precise. This highlights the difference between an exact mathematical expression and its numerical approximation.
Calculating 5√3:
While a precise calculation is impossible due to the irrational nature of √3, we can achieve high accuracy using calculators or computer software. Most scientific calculators have a square root function (√) that allows for direct computation. Alternatively, you can use iterative methods like the Babylonian method (also known as Heron's method) to approximate √3, then multiply the result by 5. This method provides successively better approximations with each iteration. However, for most practical purposes, the calculator's approximation is sufficient.
Geometric Interpretation of 5√3:
The expression 5√3 has a significant geometric interpretation. Consider an equilateral triangle with side length 'x'. The height of this triangle is given by (x√3)/2. If the height of the triangle is 5, then we can set up the equation:
(x√3)/2 = 5
Solving for 'x', we get:
x = 10/√3 or x = (10√3)/3
This demonstrates how 5√3 is intrinsically linked to the geometry of equilateral triangles and their associated dimensions. It appears in various geometric calculations involving angles of 60° and 30°. Further, it relates to the concept of a 30-60-90 triangle, a special right-angled triangle where the ratios of its sides are directly connected to √3.
Applications of 5√3:
The expression 5√3 finds its way into various fields, demonstrating its importance beyond pure mathematical theory. Let's explore some key areas:
1. Trigonometry: 5√3 frequently appears in trigonometric calculations involving angles of 30°, 60°, and their multiples. For instance, in solving for the sides or angles of a triangle using the sine, cosine, or tangent functions, you might encounter this value. It's essential in understanding the relationships between angles and side lengths in various geometric contexts.
2. Physics: In physics, particularly in mechanics and vector analysis, you might encounter 5√3 when dealing with forces, velocities, or displacements that are resolved into components. For instance, consider a force vector with a magnitude of 10 units directed at a 60° angle. Resolving this force into its horizontal and vertical components will involve calculations that directly incorporate √3, and subsequently 5√3 if the magnitude is adjusted.
3. Engineering: Civil and mechanical engineers frequently use trigonometry and geometry in their calculations. This leads to the frequent use of expressions such as 5√3 in structural design, where analyzing forces and stresses within structures often involves resolving vectors at different angles. Similarly, in surveying and mapping, calculations involving distances and angles will often lead to the appearance of √3 in the results.
4. Computer Graphics: In computer graphics and game development, transformations and rotations of objects are often defined using trigonometric functions. Consequently, the value 5√3 could be used to precisely position or scale objects within a three-dimensional space, ensuring accurate and visually consistent results.
5. Electrical Engineering: In alternating current (AC) circuits, the use of phasors to represent voltages and currents frequently leads to calculations involving trigonometric functions and subsequently, expressions like 5√3. This is particularly true when dealing with three-phase power systems where the voltage and current relationships are defined by phase angles that result in the inclusion of √3 in formulas.
Approximating 5√3:
While precision is important in many calculations, sometimes an approximation is sufficient, especially in real-world scenarios where minor discrepancies might not significantly affect the outcome. We already established that 5√3 is approximately 8.660. This approximation is accurate enough for many practical applications. However, depending on the required precision, you might need to use a more accurate approximation, which can easily be obtained using a calculator or computer software. The level of approximation needed depends entirely on the context of the problem being solved.
Beyond the Basics: Exploring Related Concepts:
Understanding 5√3 opens doors to exploring related mathematical concepts that enhance our understanding of its context and application. These include:
-
Irrational Numbers: The presence of √3 highlights the significance of irrational numbers in mathematics and their ubiquitous presence in various applications. Understanding the properties and characteristics of irrational numbers is critical to working with expressions such as 5√3.
-
Trigonometric Identities: The appearance of 5√3 is often linked to trigonometric identities, which govern the relationships between different trigonometric functions. Understanding these identities allows us to manipulate and simplify expressions involving 5√3, thereby easing calculations.
-
Vector Analysis: The resolution of vectors into their components frequently leads to calculations involving √3, particularly when dealing with angles related to equilateral triangles or 30-60-90 triangles.
-
Coordinate Geometry: The expression 5√3 might be encountered while calculating distances and lengths in coordinate geometry, especially when working with points that form equilateral or 30-60-90 triangles.
Conclusion:
The seemingly simple expression 5√3 holds a wealth of mathematical significance and finds practical applications across a wide range of fields. Its connection to geometry, trigonometry, and vector analysis makes it a cornerstone concept in various scientific and engineering disciplines. Understanding its properties, methods of calculation, and geometric interpretations is crucial for anyone seeking a deeper appreciation of fundamental mathematical principles and their impact on our world. From the precise calculations in engineering to the approximations used in everyday problem-solving, 5√3 remains a versatile and important component of the mathematical landscape. By understanding its nuances and applications, we gain a more comprehensive grasp of the interconnectedness of mathematics and the physical world.
Latest Posts
Latest Posts
-
Can Dna Leave The Nucleus
Sep 08, 2025
-
When Walking With Ambulatory Patients
Sep 08, 2025
-
Slope 2 Y Intercept 2
Sep 08, 2025
-
40 Km H In Miles
Sep 08, 2025
-
A Behavioral Description Should Include
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 5 Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.