5n 34 2 1 7n
gasmanvison
Sep 10, 2025 · 5 min read
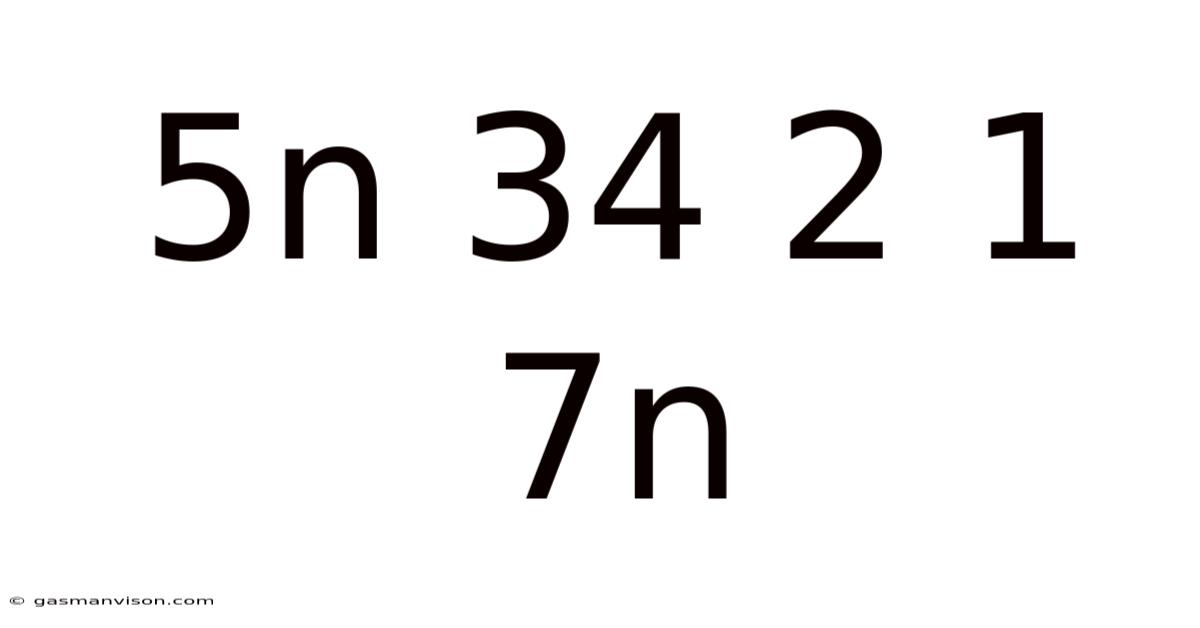
Table of Contents
Decoding the Enigma: A Deep Dive into the Sequence 5n, 34, 2, 1, 7n
The seemingly random sequence "5n, 34, 2, 1, 7n" presents a fascinating challenge. At first glance, it appears arbitrary. However, a closer examination reveals potential underlying patterns and mathematical relationships, offering a rich opportunity for exploration and analysis. This article will delve into various interpretations, exploring possible connections, mathematical structures, and the implications of this intriguing numerical arrangement. Our goal is not only to understand the sequence but also to illuminate the broader analytical strategies useful in deciphering seemingly random data sets.
What is the significance of "n"?
The presence of "n" in the sequence immediately suggests a potential for generalization. "n" likely represents a variable, implying that the sequence might be part of a larger mathematical formula or a pattern that repeats with varying values of "n." The most straightforward interpretation is that "5n" and "7n" are algebraic expressions, where "n" can be any integer or even a real number, depending on the context. This interpretation opens up possibilities for generating a whole family of sequences based on different values of "n." For example, if n=1, the sequence becomes 5, 34, 2, 1, 7. If n=2, it becomes 10, 34, 2, 1, 14. Understanding the role of "n" is key to unlocking the true nature of this sequence.
Analyzing the Constant Numbers: 34, 2, and 1
The inclusion of the constants 34, 2, and 1 adds another layer of complexity. Their presence suggests they might represent specific points of reference or pivotal values within a larger mathematical system. They could be:
- Arbitrary Constants: The simplest explanation is that these numbers are randomly chosen. However, this is less satisfying from a mathematical perspective, leaving the sequence seemingly meaningless.
- Significant Values: Alternatively, they might hold mathematical significance within a specific context. For example, 34 might be related to a particular prime number, factorial, or Fibonacci sequence. Similarly, 2 and 1 are fundamental numbers in many mathematical systems.
- Points in a Function: Another possibility is that these numbers represent specific points on a graph or function. Their relationship to the variable terms "5n" and "7n" would then determine the complete function.
Exploring Potential Mathematical Relationships
Let's explore several potential mathematical relationships that could explain the sequence:
1. Arithmetic Progression (AP): While the sequence as a whole doesn't appear to be a simple arithmetic progression (a constant difference between consecutive terms), we could analyze subsequences. For example, if we focus on just the constant terms (34, 2, 1), we do not find a consistent difference.
2. Geometric Progression (GP): Similarly, a geometric progression (a constant ratio between consecutive terms) doesn't immediately appear. Again, analyzing subsequences might yield different results.
3. Polynomial Relationship: It's possible the sequence is defined by a polynomial function. This approach would involve finding a polynomial equation that generates the terms of the sequence for different values of "n." This would require more data points (different values of "n" and their corresponding sequences) to establish a reliable polynomial fit.
4. Recursive Relationships: A more advanced approach would consider recursive relationships. This involves defining a term in the sequence based on the values of preceding terms. However, without more data points, defining such a recursive relationship would be highly speculative.
5. Modular Arithmetic: Modular arithmetic involves working with remainders after division. It's possible the sequence is related to congruences modulo some integer. This approach could explain the seemingly disparate values. We'd need to experiment with different moduli to find a potential congruence relation.
6. Number Theory Concepts: The sequence could be related to more sophisticated number theory concepts such as prime factorization, divisors, or other properties of numbers. Again, a thorough investigation using different values of "n" and analyzing the resulting sequences would be crucial.
The Importance of Context
The true meaning of the sequence "5n, 34, 2, 1, 7n" highly depends on the context in which it appears. Where did you encounter this sequence? Knowing its origin is crucial for interpreting its significance. Did it originate from a mathematical problem, a coding challenge, a data analysis task, or some other source? The context drastically influences the methods we use to analyze it.
Strategies for Further Investigation
To further investigate this sequence, we can employ the following strategies:
- Generate More Data: The most important step is to obtain more data points by varying the value of "n" and observing the resulting sequences. A larger dataset significantly improves the chances of discovering hidden patterns.
- Visual Representation: Plotting the sequence on a graph (with "n" on the x-axis and the sequence terms on the y-axis) might reveal hidden patterns or trends.
- Statistical Analysis: Statistical methods, such as correlation analysis or regression analysis, could identify relationships between different terms in the sequence.
- Computer Programming: Writing a simple computer program to generate sequences for different "n" values and analyze the resulting data would greatly enhance efficiency.
Conclusion: The Power of Mathematical Inquiry
The sequence "5n, 34, 2, 1, 7n" serves as an excellent example of how seemingly simple sequences can lead to complex mathematical investigations. The presence of the variable "n" and the constants introduce various possibilities, highlighting the importance of utilizing different analytical techniques to uncover underlying patterns. Without further context or data, a definitive answer remains elusive. However, the process of exploring potential mathematical relationships and applying various analytical strategies underscores the inherent power and beauty of mathematical inquiry. The solution lies not only in finding a single answer, but also in understanding the process of discovery and the potential for uncovering hidden structures within seemingly random numerical arrangements. The exploration itself is a testament to the enduring fascination of mathematics and its ability to challenge and reward those who dare to delve into its depths.
Latest Posts
Latest Posts
-
60 Degrees C In F
Sep 10, 2025
-
Electron Dot Diagram Of Oxygen
Sep 10, 2025
-
Draw Sheets Are Used To
Sep 10, 2025
-
Is Hexane Polar Or Nonpolar
Sep 10, 2025
-
Un Automovilista Debe Saber Que
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5n 34 2 1 7n . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.