6 1/2 Divided By 3/2
gasmanvison
Sep 18, 2025 · 5 min read
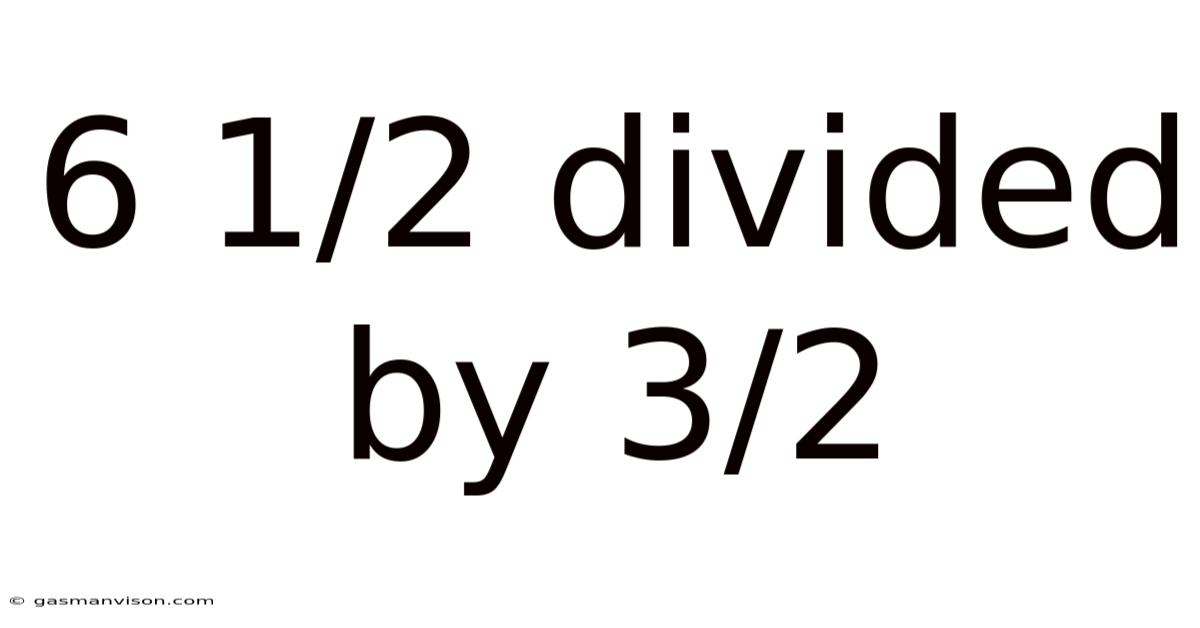
Table of Contents
6 1/2 Divided by 3/2: A Comprehensive Guide to Fraction Division
This article will delve into the seemingly simple yet often confusing topic of dividing mixed numbers: specifically, 6 1/2 divided by 3/2. We'll explore multiple methods for solving this problem, explaining the underlying mathematical principles and offering practical tips to master fraction division. Understanding this concept is crucial for anyone working with fractions, from students mastering elementary math to professionals needing to perform precise calculations. This guide aims to provide a complete understanding, ensuring you can tackle similar problems with confidence.
What We'll Cover:
- Understanding Mixed Numbers and Improper Fractions
- Method 1: Converting to Improper Fractions
- Method 2: Using the "Keep, Change, Flip" Method
- Method 3: Converting to Decimals (with caveats)
- Real-World Applications of Fraction Division
- Troubleshooting Common Mistakes
- Expanding Your Understanding: Further Challenges
Understanding Mixed Numbers and Improper Fractions
Before we tackle the division problem, let's solidify our understanding of the terms involved. A mixed number combines a whole number and a fraction (e.g., 6 1/2). An improper fraction has a numerator larger than or equal to its denominator (e.g., 13/2). These two forms are interchangeable; knowing how to convert between them is essential for effective fraction manipulation.
To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same. For 6 1/2:
(6 * 2) + 1 = 13 Therefore, 6 1/2 = 13/2
Conversely, to convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction, with the denominator remaining the same.
Method 1: Converting to Improper Fractions
This is the most common and generally preferred method for dividing mixed numbers. It involves converting both the mixed number and the fraction to improper fractions before performing the division.
-
Convert the mixed number: As shown above, 6 1/2 converts to 13/2.
-
Keep the second fraction: The second fraction, 3/2, remains as it is.
-
Invert and multiply: Dividing by a fraction is the same as multiplying by its reciprocal (flipped fraction). So, we change the division to multiplication and flip the second fraction:
13/2 ÷ 3/2 = 13/2 * 2/3
-
Simplify and multiply: Notice that we can simplify before multiplying. Both the numerator of the first fraction (13) and the denominator of the second fraction (2) can be divided by 2.
(13/2) * (2/3) = (13/1) * (1/3) = 13/3
-
Convert to a mixed number: Finally, convert the improper fraction 13/3 to a mixed number:
13 ÷ 3 = 4 with a remainder of 1. Therefore, 13/3 = 4 1/3
Therefore, 6 1/2 divided by 3/2 equals 4 1/3.
Method 2: Using the "Keep, Change, Flip" Method
This method is a shortcut that directly addresses the division of fractions without explicitly converting to improper fractions first. It's particularly useful for those comfortable working with mixed numbers.
-
Keep: Keep the first mixed number (6 1/2) as it is.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (reciprocate) the second fraction (3/2) to become 2/3.
-
Multiply: Now multiply the first mixed number by the flipped second fraction. This can be done in a few ways. You can either convert 6 1/2 to an improper fraction first (as in Method 1), or you can distribute the multiplication:
6 1/2 × 2/3 = (6 × 2/3) + (1/2 × 2/3) = 4 + 1/3 = 4 1/3
Again, the answer is 4 1/3.
Method 3: Converting to Decimals (with caveats)
While possible, converting to decimals is generally less precise and less preferred for fraction division, especially when dealing with fractions that don't convert to terminating decimals.
-
Convert to decimals: 6 1/2 = 6.5 and 3/2 = 1.5
-
Divide: 6.5 ÷ 1.5 ≈ 4.333...
This method yields an approximate answer due to the repeating decimal. While suitable for some applications, it lacks the precision and elegance of the fraction methods. It's best to stick with methods 1 and 2 for accurate results, especially when dealing with exact fractions.
Real-World Applications of Fraction Division
Understanding fraction division is vital in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down requires dividing fractional quantities.
- Sewing and Crafting: Cutting fabric or other materials to precise fractional lengths involves division.
- Construction and Engineering: Precise measurements in construction frequently involve fractions and their division.
- Finance and Budgeting: Dividing resources or budgets often involves fractional components.
Troubleshooting Common Mistakes
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before dividing.
- Incorrectly inverting the second fraction: Make sure to flip the second fraction, not the first.
- Not simplifying before multiplying: Simplifying fractions before multiplication makes the calculation easier and reduces the risk of errors.
- Rounding errors with decimals: Avoid relying solely on decimal conversions, especially when dealing with repeating decimals.
Expanding Your Understanding: Further Challenges
Once you've mastered dividing 6 1/2 by 3/2, try these challenges to solidify your understanding:
- Divide 8 3/4 by 2 1/2
- Solve 5/8 divided by 1 1/4
- A recipe calls for 2 1/3 cups of flour. If you want to make half the recipe, how much flour do you need?
- A piece of wood is 12 1/2 feet long. You need to cut it into pieces that are 1 1/4 feet long. How many pieces can you cut?
By working through these examples and applying the methods outlined above, you’ll develop a strong foundation in fraction division and its practical applications. Remember, practice is key to mastering any mathematical concept. The more you work with fractions, the more comfortable and confident you'll become.
Latest Posts
Latest Posts
-
What Is 10 Of 150 00
Sep 18, 2025
-
60 Degrees Fahrenheit In Celsius
Sep 18, 2025
-
770 070 In Word Form
Sep 18, 2025
-
104 Degree Fahrenheit To Celsius
Sep 18, 2025
-
What Is 5 Of 1000000
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 6 1/2 Divided By 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.