6 11 As A Decimal
gasmanvison
Sep 25, 2025 · 5 min read
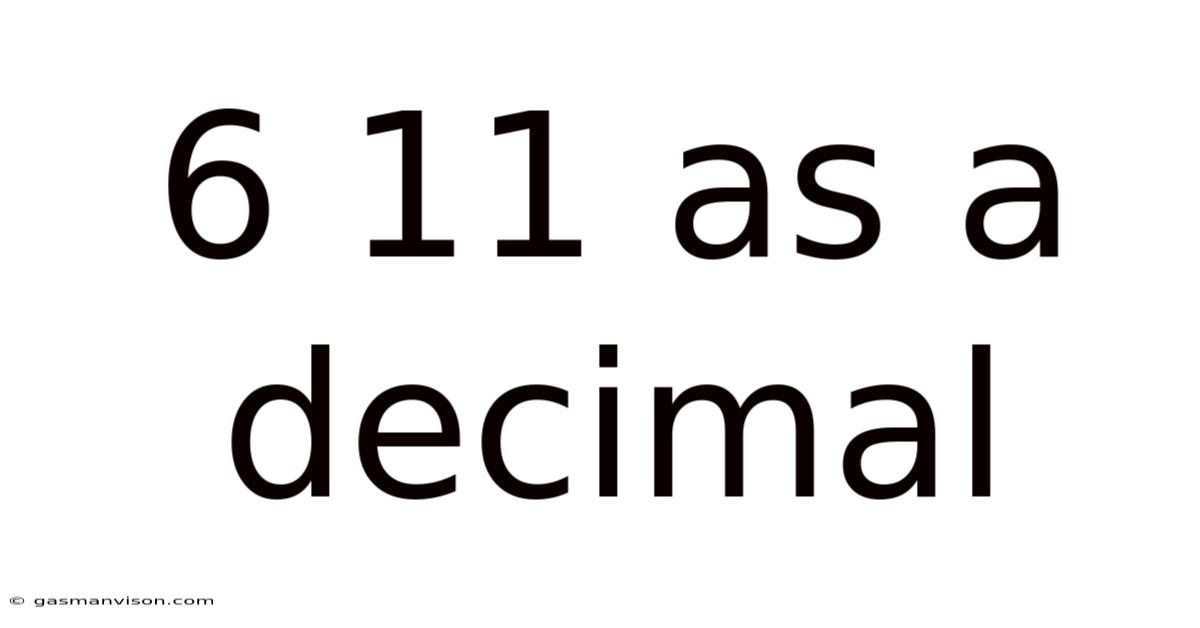
Table of Contents
Decoding 6/11 as a Decimal: A Comprehensive Guide
Meta Description: Learn how to convert the fraction 6/11 into a decimal, exploring different methods including long division and understanding the concept of repeating decimals. This guide provides a thorough explanation and practical examples for both beginners and advanced learners.
Converting fractions to decimals is a fundamental skill in mathematics with wide-ranging applications in various fields. While some fractions convert neatly into terminating decimals, others result in repeating decimals. This article delves deep into the conversion of the fraction 6/11 into its decimal equivalent, exploring the process, the nature of the resulting decimal, and its significance in practical contexts. We'll break down the process step-by-step, ensuring a clear understanding for everyone, from students just learning about fractions to those seeking a refresher on decimal conversions.
Understanding Fractions and Decimals
Before diving into the conversion of 6/11, let's briefly recap the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). Decimals use a decimal point to separate the whole number part from the fractional part.
The fundamental relationship between fractions and decimals is that every fraction can be expressed as a decimal, and vice-versa. This conversion is crucial for various mathematical operations and real-world applications, such as calculating percentages, working with measurements, and solving problems involving proportions.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is long division. To convert 6/11 to a decimal, we divide the numerator (6) by the denominator (11):
0.545454...
11 | 6.000000
-5.5
-----
0.50
-0.44
-----
0.060
-0.055
-----
0.0050
-0.0044
-----
0.00060
...and so on...
As you can see, the division process continues indefinitely, with the digits "54" repeating. This is a repeating decimal, also known as a recurring decimal.
Understanding Repeating Decimals
A repeating decimal is a decimal representation of a number that has a sequence of digits that repeat infinitely. This repeating sequence is often indicated by placing a bar over the repeating digits. Therefore, 6/11 as a decimal is written as:
0.54̅
The bar above the "54" indicates that the sequence "54" repeats infinitely. It's crucial to understand that this doesn't mean the decimal stops at "54"; it continues with "545454..." without end.
Method 2: Using a Calculator
While long division provides a conceptual understanding, a calculator offers a quicker way to obtain the decimal equivalent. Simply enter 6 ÷ 11 into your calculator. The result will be displayed as 0.545454... or a similar representation, depending on the calculator's display capabilities. Many calculators will round the decimal after a certain number of digits, but the true value remains a repeating decimal.
Significance of Repeating Decimals
The fact that 6/11 results in a repeating decimal highlights an important aspect of number systems. Not all fractions can be expressed as terminating decimals (decimals that end). Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals. Since 11 is a prime number (it's only divisible by 1 and itself), it leads to a repeating decimal when used as a denominator.
Applications of Decimal Conversion
The conversion of fractions to decimals is crucial in numerous applications:
- Financial Calculations: Calculating interest, discounts, and profits often involves working with decimal values.
- Engineering and Science: Measurements and calculations in engineering and scientific fields frequently require decimal precision.
- Computer Programming: Many programming languages require decimal representation for numerical data.
- Data Analysis: Statistical analysis often involves working with decimal data.
- Everyday Life: Percentages, which are essentially fractions expressed as decimals (multiplied by 100), are used in everyday contexts like sales, taxes, and tips.
Different Representations of Repeating Decimals
While 0.54̅ is the most common representation, there are other ways to express repeating decimals:
- Using parentheses: 0.(54) indicates that 54 repeats infinitely.
- Using ellipses: 0.545454... shows the repetition with ellipses.
- As a fraction: The most accurate representation is the original fraction, 6/11. This avoids any rounding errors associated with truncating the repeating decimal.
Practical Examples Using 6/11 as a Decimal
Let's illustrate the practical application of converting 6/11 to its decimal equivalent:
Example 1: Calculating a Discount
A store offers a 6/11 discount on an item priced at $110. To calculate the discount, we multiply the price by the decimal equivalent of 6/11:
$110 * 0.545454... ≈ $60
Example 2: Dividing a Quantity
We have 66 apples and want to divide them equally among 11 people. The number of apples each person receives can be calculated using the fraction 66/11, which simplifies to 6. Alternatively, we can use the decimal representation: 66 / 11 = 6.
Example 3: Calculating a Percentage
To express 6/11 as a percentage, we multiply the decimal equivalent by 100:
0.545454... * 100 ≈ 54.55%
Conclusion
Converting 6/11 to its decimal equivalent, 0.54̅, highlights the importance of understanding both fractions and decimals and their interrelationship. The process, whether through long division or using a calculator, demonstrates the concept of repeating decimals and their practical implications in various fields. While calculators provide a quick solution, the understanding of long division offers a deeper appreciation of the mathematical principles involved. Remember that while truncating or rounding the repeating decimal might be necessary in certain applications, the original fraction 6/11 remains the most precise representation. Mastering this conversion strengthens foundational mathematical skills essential for numerous real-world applications.
Latest Posts
Latest Posts
-
Lewis Dot Structure For Chcl3
Sep 25, 2025
-
Informational Social Influence Occurs Because
Sep 25, 2025
-
Net Worth Of Jesse Jackson
Sep 25, 2025
-
Is Nether Travel 8 Blocks
Sep 25, 2025
-
How Many Mg Is 1ml
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 6 11 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.