6 4x 6x 8x 2
gasmanvison
Sep 25, 2025 · 5 min read
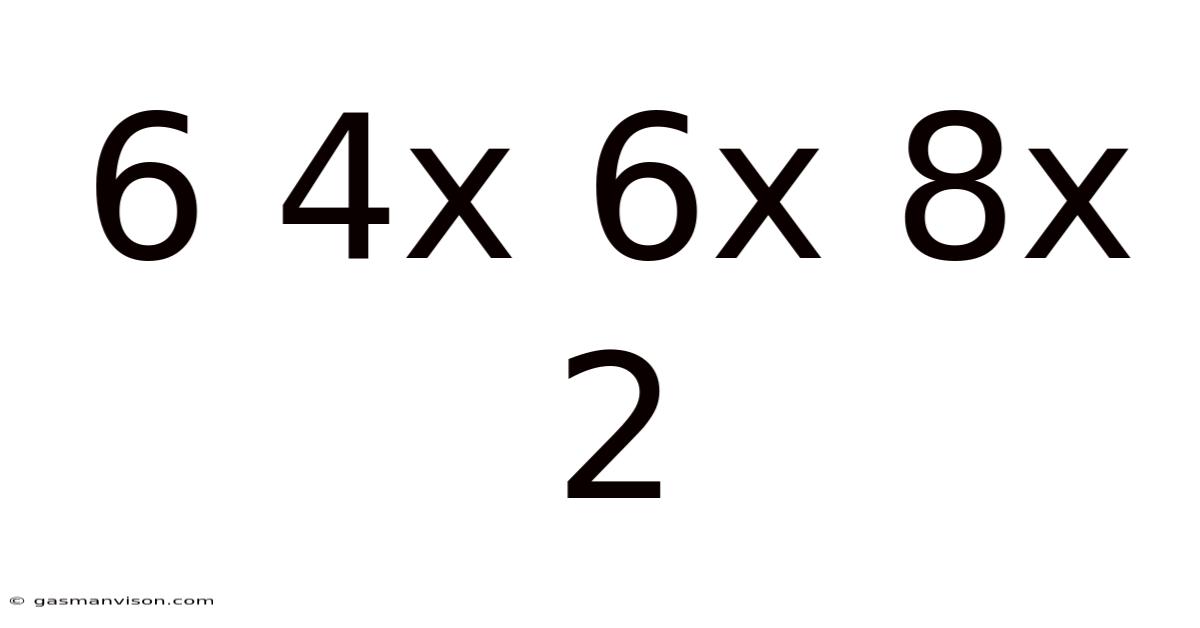
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Practical Implications of "6 4x 6x 8x 2"
This seemingly simple string of numbers, "6 4x 6x 8x 2," presents a fascinating challenge. At first glance, it appears to be a straightforward mathematical expression. However, a deeper dive reveals potential interpretations within various fields, from basic arithmetic to more complex geometrical and logistical problems. This article will explore the multiple meanings and applications of this numerical sequence, delving into its mathematical solutions, potential practical applications, and the importance of precise notation in problem-solving.
What the Expression Could Mean: A Multifaceted Interpretation
The core ambiguity lies in the lack of defined operators between the numbers. Is it a series of multiplications? Does it incorporate addition or subtraction? The possibilities are numerous, leading to a range of potential solutions. Let's explore some of the most likely interpretations:
1. A Sequence of Multiplications:
The most straightforward interpretation treats the 'x' symbols as multiplication signs. In this case, the calculation would proceed as follows:
6 x 4 x 6 x 8 x 2 = 2304
This solution is relatively simple and yields a single, definitive answer. This interpretation is useful in contexts where a straightforward calculation is needed, such as in basic arithmetic exercises or in simple inventory calculations (e.g., calculating the total number of items given 6 boxes of 4, 6 boxes of 6, 8 boxes of 8, and 2 boxes of 2 items each).
2. A Combination of Operations:
The absence of explicit operators opens the door to more complex interpretations. For instance, the expression could represent a combination of multiplication, addition, and subtraction. Different order of operations could lead to drastically different results. For example:
(6 x 4) + (6 x 8) x 2 = 1206 x (4 + 6) x (8 x 2) = 9606 x 4 x 6 - 8 + 2 = 144 - 8 + 2 = 138
This highlights the crucial role of clear and unambiguous notation in mathematical expressions. Without parentheses or explicit operators, the meaning becomes subjective, leading to multiple, potentially vastly different, results.
3. Geometric or Spatial Interpretation:
The numbers could represent dimensions or quantities related to a three-dimensional object or space. For instance, the sequence might represent:
- Dimensions of a Rectangular Prism: Imagine a series of rectangular prisms with dimensions 6x4x6, 6x8x2, and so on. Calculating the volume of each prism and then summing them would yield a combined volume. This interpretation is particularly relevant in fields like architecture, engineering, or logistics where the calculation of space is critical.
- Number of Objects in a Grid: The numbers could signify the arrangement of objects in a multi-dimensional grid. Understanding the arrangement and calculating the total number of objects would require careful consideration of the spatial relationships implied by the numbers.
4. Data Sequence in Programming or Data Analysis:
In the context of computer programming or data analysis, the sequence "6 4x 6x 8x 2" might represent a list or array of data points. The 'x' could be a separator rather than an operator. The interpretation would depend entirely on the context and the algorithm processing this data. The analysis might involve calculating the mean, median, standard deviation, or other relevant statistical measures.
The Importance of Precise Notation and the Order of Operations (PEMDAS/BODMAS)
The ambiguity in the given expression underscores the critical importance of clear and consistent mathematical notation. The lack of clearly defined operators necessitates a deeper understanding of the order of operations, commonly represented by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These rules dictate the sequence in which operations should be performed to obtain a consistent and unambiguous result. Without these rules, the same expression could be interpreted in multiple ways, leading to different solutions.
Practical Applications and Real-World Scenarios
While the expression "6 4x 6x 8x 2" might seem abstract, its components find applications across various fields. Let's explore some scenarios:
- Inventory Management: Imagine a warehouse managing different types of boxes. Each number could represent the quantity of boxes with specific dimensions or contents. Calculating the total storage space needed would involve the principles of multiplication and potentially addition depending on the stacking arrangements.
- Construction and Engineering: The numbers could represent dimensions of materials required for a construction project, such as beams, bricks, or tiles. Accurate calculation of quantities is crucial for efficient resource allocation and cost management.
- Packaging and Logistics: In shipping and logistics, the numbers could be associated with the dimensions of packages, the number of items per package, or the number of packages per pallet. Optimization of package size and weight is crucial for efficient shipping and transportation.
- Manufacturing and Production: The numbers could relate to the dimensions of components in a manufacturing process. Understanding these dimensions is crucial for accurate production and quality control.
- Data Analysis and Statistics: As mentioned before, the sequence could represent a set of data points in a larger data set, necessitating statistical analysis for further insights.
Expanding the Analysis: Exploring Related Concepts
The numerical sequence "6 4x 6x 8x 2" can serve as a springboard for exploring broader mathematical concepts:
- Factorials: While not directly relevant to the given expression, the concept of factorials (e.g., 6!) could be used to explore related combinatorial problems involving permutations and combinations.
- Prime Factorization: Breaking down the individual numbers (6, 4, 6, 8, 2) into their prime factors (2, 3) provides a deeper understanding of their inherent mathematical properties.
- Modular Arithmetic: Exploring the remainders after dividing the result by various numbers (e.g., modulo 10) could reveal patterns and relationships.
Conclusion: The Power of Precise Communication in Mathematics
The ambiguity presented by "6 4x 6x 8x 2" highlights the profound importance of clear and precise communication in mathematics and related fields. The absence of clearly defined operators leads to multiple interpretations and vastly different solutions. To avoid such ambiguity, using parentheses and explicitly defining the operations between numbers is crucial. This exercise emphasizes the need for careful notation, a strong understanding of the order of operations, and context-aware interpretation to arrive at accurate and meaningful results. The seemingly simple expression can become a powerful tool for understanding mathematical concepts and their real-world applications, provided that ambiguity is eliminated through careful notation and clear definitions. The potential applications extend far beyond simple arithmetic, touching upon geometry, logistics, and data analysis, highlighting the multifaceted nature of even the simplest numerical sequences.
Latest Posts
Latest Posts
-
Formula For Iron 3 Sulfide
Sep 25, 2025
-
1 2 Cup Divided By 3
Sep 25, 2025
-
Learning Through Art Lipid Structure
Sep 25, 2025
-
S Is Close To Retiring
Sep 25, 2025
-
Clo Lewis Structure Formal Charge
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 6 4x 6x 8x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.