6 9 13 20 31
gasmanvison
Sep 25, 2025 · 6 min read
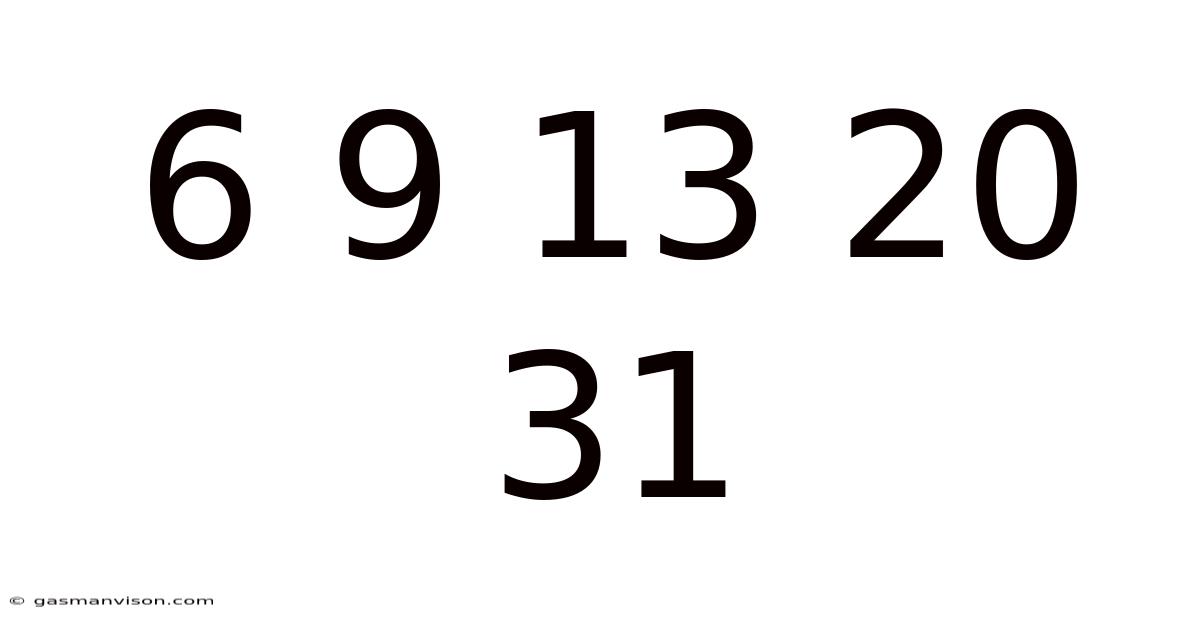
Table of Contents
Unraveling the Sequence: Exploring the Mathematical Beauty and Potential Patterns of 6, 9, 13, 20, 31
The seemingly simple sequence 6, 9, 13, 20, 31 holds a surprising depth of mathematical possibilities. At first glance, it appears random, but a closer examination reveals potential patterns and underlying structures that can lead to intriguing explorations in number theory and sequence analysis. This article delves into various methods of analyzing this sequence, considering different approaches to identify potential rules, generating future terms, and discussing the limitations of these methods. Understanding sequences like this helps develop critical thinking skills, fosters an appreciation for mathematical patterns, and demonstrates the power of different analytical techniques.
Meta Description: Discover the hidden patterns and mathematical possibilities within the intriguing number sequence 6, 9, 13, 20, 31. Explore various methods for analyzing this sequence, including difference analysis, recursive relations, and potential generating functions. Uncover the challenges and limitations in predicting future terms, and appreciate the beauty of mathematical exploration.
Method 1: Difference Analysis – Unveiling the Hidden Increments
A fundamental approach to analyzing a numerical sequence is to examine the differences between consecutive terms. Let's apply this method to our sequence:
- 9 - 6 = 3
- 13 - 9 = 4
- 20 - 13 = 7
- 31 - 20 = 11
The differences themselves form a new sequence: 3, 4, 7, 11. This sequence doesn't immediately reveal a clear pattern, but let's continue the difference analysis by examining the differences between these differences:
- 4 - 3 = 1
- 7 - 4 = 3
- 11 - 7 = 4
We now have a sequence of differences: 1, 3, 4. Again, no immediately obvious pattern jumps out. This approach, while providing insights into the rate of growth of the original sequence, doesn't definitively reveal a simple, closed-form formula to generate future terms. However, the fluctuating differences suggest a more complex underlying relationship than a simple arithmetic or geometric progression. This highlights the limitations of solely relying on difference analysis for complex sequences.
Method 2: Recursive Relationships – Defining Terms Based on Predecessors
A recursive relationship defines a term in a sequence based on one or more preceding terms. While we haven't found a straightforward pattern in the differences, let's explore if a recursive relationship exists. One possible approach is to explore combinations of preceding terms. For example:
- 6 + 3 = 9
- 9 + 4 = 13
- 13 + 7 = 20
- 20 + 11 = 31
Notice the pattern in the additions: 3, 4, 7, 11. These are the first differences we calculated earlier. This suggests a recursive relation where the next term is the sum of the current term and the difference between the previous two terms. However, defining the sequence entirely recursively requires establishing a starting point (the first two terms) and a rule for generating subsequent terms. The inherent recursive nature itself doesn't lend itself to a neat closed-form expression, but it does offer a way to generate more terms within the sequence.
To explore this further, let's try to formalize this recursive relationship. Let the sequence be denoted by a<sub>n</sub>. We can tentatively suggest a recursive relation of the form:
a<sub>n</sub> = a<sub>n-1</sub> + (a<sub>n-1</sub> - a<sub>n-2</sub>) + f(n)
where f(n) represents a function that adds to the calculated difference to maintain the established sequence. However, determining this f(n) function to precisely predict future numbers requires a deeper understanding, which may not be readily apparent.
Method 3: Exploring Potential Generating Functions – A More Advanced Approach
Generating functions provide a powerful tool for analyzing sequences. They represent a sequence as a formal power series, where the coefficients correspond to the terms of the sequence. Finding a closed-form expression for a generating function can significantly simplify the process of identifying the nth term. However, for sequences like this, finding a suitable generating function can be challenging and often requires advanced mathematical techniques. The apparent lack of an easily identifiable pattern makes finding a generating function quite intricate and potentially beyond the scope of elementary methods.
This method emphasizes that while theoretically powerful, generating functions are not always practical for every sequence. The sequence’s irregularity demands more sophisticated mathematical tools which are beyond the scope of a general analysis.
Method 4: Considering Fibonacci-Like Relationships – Exploring Similar Sequences
While the sequence doesn't directly follow the Fibonacci sequence (where each term is the sum of the two preceding terms), it’s worth exploring if similar recursive relationships based on sums of preceding terms might exist. This requires experimenting with different combinations and weights assigned to previous terms, but this trial-and-error approach is not guaranteed to yield a definitive formula.
This highlights the importance of recognizing that not all sequences conform to well-known mathematical structures. The lack of a readily apparent Fibonacci-like or other simple recursive pattern again underscores the sequence's complexity.
Limitations and Challenges in Predicting Future Terms
The analysis reveals that while different approaches provide insights into the sequence's structure, precisely predicting future terms remains challenging. The absence of a readily apparent, simple, closed-form formula prevents us from directly calculating the nth term. The recursive relationship we attempted to define, while providing a method for generating further terms, still depends on determining a function that we haven't yet identified.
Furthermore, the difference analysis, though suggestive, doesn't lead to a consistent and easily identifiable pattern. While generating functions are a powerful theoretical tool, finding one suitable for this sequence is not straightforward.
These limitations highlight the importance of acknowledging the complexity inherent in some mathematical sequences. Not all sequences conform to easily identifiable patterns, and this emphasizes the need for diverse analytical approaches and the potential for multiple interpretations.
Conclusion: The Value of Mathematical Exploration
The sequence 6, 9, 13, 20, 31, while seemingly simple, provides a fascinating case study in mathematical exploration. The challenges encountered in identifying a definitive pattern or closed-form expression highlight the limitations of even seemingly straightforward analytical techniques. The lack of a simple solution doesn’t diminish the value of the exploration. The process itself enhances our understanding of numerical sequences, reinforces critical thinking skills, and demonstrates the power – and limitations – of different mathematical approaches. Future investigations might involve the use of more advanced mathematical tools or exploring connections to other areas of mathematics, such as chaos theory, where seemingly random patterns can exhibit underlying structures. The beauty of mathematics often lies not just in finding solutions, but in the journey of exploration and discovery itself. The apparent randomness of this sequence ultimately underscores the diversity and richness of mathematical patterns waiting to be uncovered.
Latest Posts
Latest Posts
-
Each Graph Shows A Relation
Sep 25, 2025
-
Lewis Dot Structure For Chcl3
Sep 25, 2025
-
Informational Social Influence Occurs Because
Sep 25, 2025
-
Net Worth Of Jesse Jackson
Sep 25, 2025
-
Is Nether Travel 8 Blocks
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 6 9 13 20 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.