7 1/3 X 2 2/11
gasmanvison
Sep 06, 2025 · 5 min read
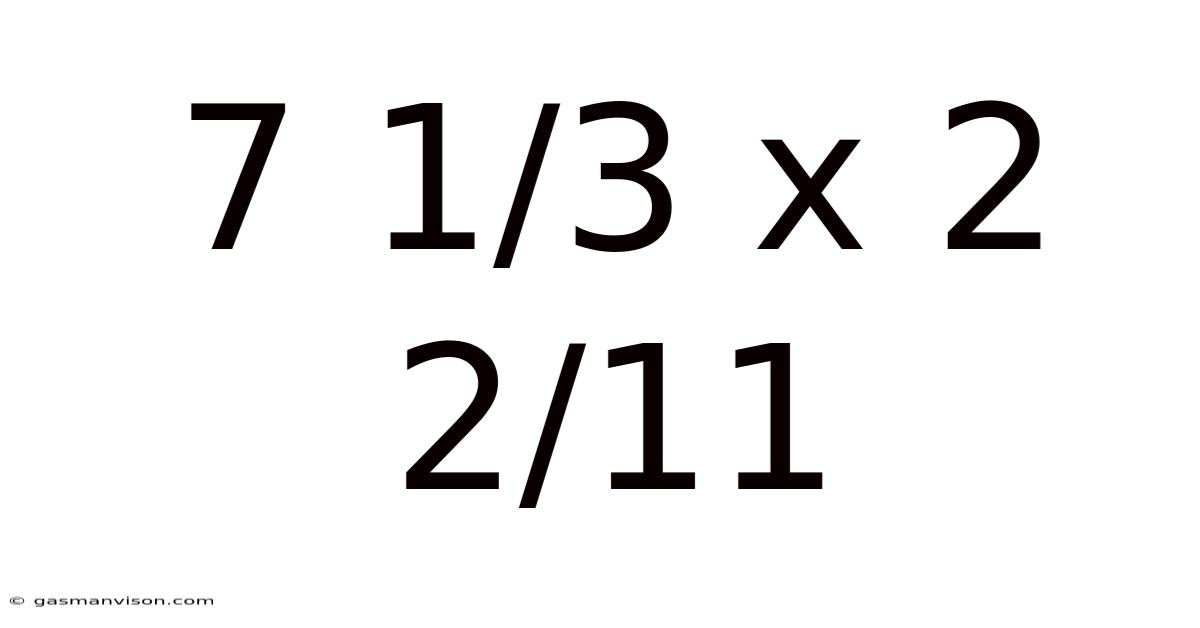
Table of Contents
Decoding 7 1/3 x 2 2/11: A Deep Dive into Mixed Number Multiplication
This article explores the seemingly simple problem of multiplying mixed numbers: 7 1/3 x 2 2/11. While the calculation itself might seem straightforward, it provides a fantastic opportunity to delve into the fundamentals of fraction manipulation, mixed number conversion, and the broader context of mathematical operations. We'll not only solve the problem but also examine different approaches, highlighting the strengths and weaknesses of each method, and emphasizing the importance of understanding the underlying principles. This understanding is crucial not just for solving this specific problem, but for tackling a wide range of more complex mathematical challenges.
Understanding Mixed Numbers
Before diving into the multiplication, let's refresh our understanding of mixed numbers. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our problem, 7 1/3 and 2 2/11 are both mixed numbers. 7 1/3 represents 7 whole units and an additional 1/3 of a unit. Similarly, 2 2/11 represents 2 whole units and 2/11 of a unit.
Method 1: Converting to Improper Fractions
This is arguably the most common and generally preferred method for multiplying mixed numbers. The process involves converting each mixed number into an improper fraction (a fraction where the numerator is larger than or equal to the denominator).
-
Converting 7 1/3: We multiply the whole number (7) by the denominator (3), add the numerator (1), and keep the same denominator (3). This gives us (7 x 3) + 1 = 22, so 7 1/3 becomes 22/3.
-
Converting 2 2/11: Similarly, we multiply the whole number (2) by the denominator (11), add the numerator (2), and keep the same denominator (11). This gives us (2 x 11) + 2 = 24, so 2 2/11 becomes 24/11.
Now, we multiply the two improper fractions:
(22/3) x (24/11) = (22 x 24) / (3 x 11) = 528 / 33
This improper fraction can be simplified by finding the greatest common divisor (GCD) of 528 and 33. The GCD is 33. Dividing both the numerator and denominator by 33, we get:
528 / 33 = 16
Therefore, 7 1/3 x 2 2/11 = 16.
Method 2: Distributive Property
While less frequently used for this type of problem, the distributive property can be applied. This method involves expanding the mixed numbers and then applying the distributive law. It's more conceptually complex but demonstrates a deeper understanding of mathematical principles.
Let's rewrite the problem as:
(7 + 1/3) x (2 + 2/11)
Now, using the distributive property (FOIL method), we multiply each term:
(7 x 2) + (7 x 2/11) + (1/3 x 2) + (1/3 x 2/11)
= 14 + 14/11 + 2/3 + 2/33
To add these fractions, we need a common denominator, which is 33:
= 14 + (14 x 3)/33 + (2 x 11)/33 + 2/33
= 14 + 42/33 + 22/33 + 2/33
= 14 + 66/33
Since 66/33 = 2, we have:
= 14 + 2 = 16
Therefore, using the distributive property, we again arrive at the answer 16.
Method 3: Estimation and Approximation
Before performing the exact calculation, estimating the answer can be valuable. This helps to check the reasonableness of the final result.
We can round 7 1/3 to 7 and 2 2/11 to 2. Multiplying these rounded numbers gives us 7 x 2 = 14. This provides a rough estimate. Since our exact answer is 16, the estimate is reasonably close. This method is useful for quickly determining if your calculated answer is in the right ballpark. This is especially useful in more complex problems or when dealing with large numbers. It helps in identifying potential errors early on.
Comparing the Methods
Each method offers a unique approach to solving the problem. The method of converting to improper fractions is generally the most efficient and straightforward for most students. The distributive property showcases a deeper understanding of mathematical principles but can be more time-consuming, especially with more complex mixed numbers. Estimation provides a valuable check for accuracy and helps build intuition around number manipulation.
Beyond the Calculation: Practical Applications and Further Exploration
The multiplication of mixed numbers isn't just an abstract mathematical exercise. It has various real-world applications:
-
Measurement and Construction: Imagine calculating the area of a rectangular room with dimensions of 7 1/3 feet by 2 2/11 feet. This problem directly relates to the multiplication of mixed numbers.
-
Cooking and Baking: Recipes often involve fractional amounts of ingredients. Multiplying mixed numbers is essential when scaling recipes up or down.
-
Finance: Calculating compound interest or dealing with fractional shares in investments might involve mixed number multiplication.
This seemingly simple problem opens doors to a wealth of mathematical concepts. Further exploration could include:
-
Working with more complex mixed numbers: Try multiplying mixed numbers with larger whole numbers and fractions with larger denominators.
-
Exploring different types of fractions: Investigate operations involving improper fractions, decimals, and percentages, understanding their interrelationships.
-
Applying the concepts to solving word problems: Develop problem-solving skills by applying these mathematical concepts to real-world scenarios.
Conclusion
The multiplication of 7 1/3 by 2 2/11, seemingly a basic arithmetic problem, provides a rich learning experience. Through exploring different solution methods—converting to improper fractions, using the distributive property, and employing estimation—we gain a deeper understanding of mixed number manipulation and the underlying mathematical principles. This understanding extends beyond the confines of this specific problem, providing a strong foundation for tackling more complex mathematical challenges in various contexts. The key takeaway is not just the answer (16), but the journey of understanding the various approaches and appreciating the practical applications of these fundamental mathematical skills. Remember to always check your work and consider using estimation as a tool to verify the reasonableness of your final answer.
Latest Posts
Latest Posts
-
7 5 4 Simulating A Coin Flip
Sep 06, 2025
-
21 Degrees Celcius To Farenheit
Sep 06, 2025
-
Convert 45 To A Decimal
Sep 06, 2025
-
Which Describes How Radiation Moves
Sep 06, 2025
-
240 Ml To Fl Oz
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 7 1/3 X 2 2/11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.