7 15 As A Decimal
gasmanvison
Sep 20, 2025 · 5 min read
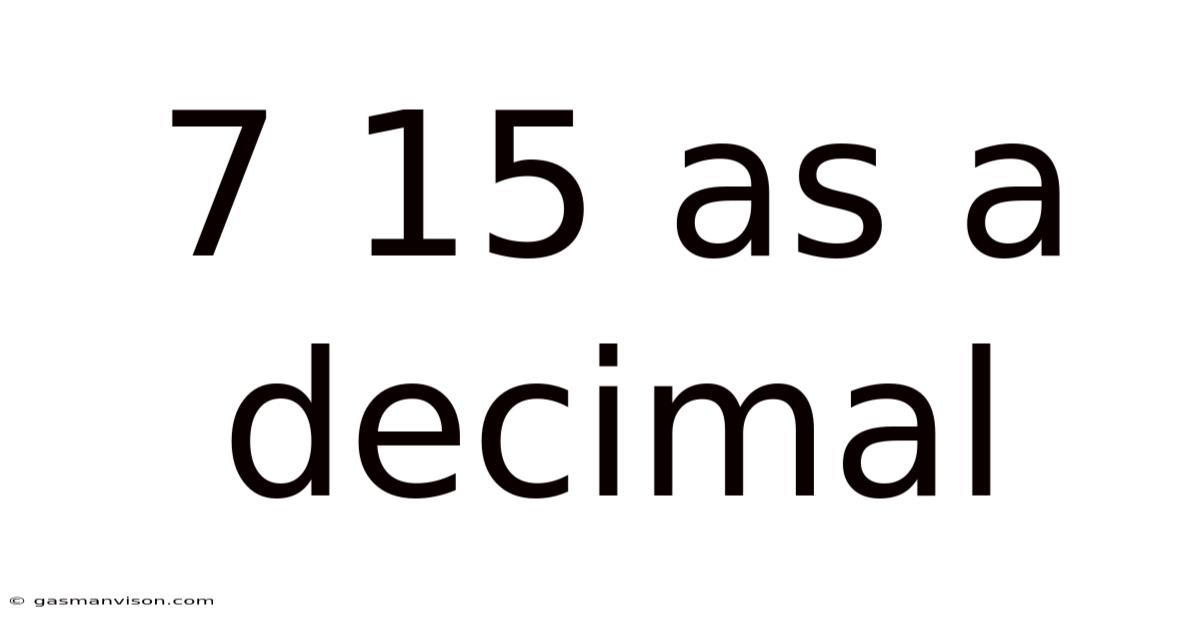
Table of Contents
7/15 as a Decimal: A Comprehensive Guide to Fraction Conversion
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve deep into the conversion of the fraction 7/15 into its decimal equivalent, exploring various methods and providing a thorough understanding of the underlying principles. This will also explore related concepts and applications, making this a valuable resource for students and anyone interested in improving their mathematical understanding.
Understanding Fractions and Decimals
Before diving into the conversion, let's briefly revisit the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (e.g., 10, 100, 1000). Decimals are expressed using a decimal point, separating the whole number part from the fractional part.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. In this method, the numerator (7) is divided by the denominator (15).
-
Set up the division: Write 7 as the dividend and 15 as the divisor. Since 7 is smaller than 15, you'll add a decimal point to 7 and add zeros as needed.
-
Perform the division: 15 goes into 7 zero times. Add a decimal point to the quotient (above the 7) and a zero to the dividend (making it 70). 15 goes into 70 four times (15 x 4 = 60). Subtract 60 from 70, leaving a remainder of 10.
-
Continue the division: Add another zero to the remainder (making it 100). 15 goes into 100 six times (15 x 6 = 90). Subtract 90 from 100, leaving a remainder of 10.
-
Recognize the pattern: Notice that the remainder is 10 again. This indicates a repeating decimal.
-
Express the result: The decimal representation of 7/15 is 0.466666... This can be written as 0.46, or more precisely as 0.466̅, where the bar indicates the repeating digit (6).
Method 2: Converting to an Equivalent Fraction with a Power of 10 Denominator
While long division is reliable, it's not always the most efficient method. An alternative approach involves converting the fraction into an equivalent fraction with a denominator that's a power of 10. Unfortunately, this method isn't directly applicable to 7/15 because 15 doesn't easily convert to a power of 10. The prime factorization of 15 is 3 x 5, and to make it a power of 10, we would need additional factors of 2. However, this illustrates the limitations of this method for certain fractions.
Let's illustrate with a fraction where this is possible, for example 3/5. We can multiply both the numerator and the denominator by 2 to get 6/10. This is easily expressed as a decimal: 0.6
Method 3: Using a Calculator
The simplest way to convert 7/15 to a decimal is by using a calculator. Simply divide 7 by 15, and the calculator will display the decimal equivalent: 0.466666...
Understanding Repeating Decimals
The decimal representation of 7/15 (0.466666...) is a repeating decimal, also known as a recurring decimal. This means a digit or sequence of digits repeats infinitely. Understanding repeating decimals is crucial when working with fractions. Not all fractions result in repeating decimals; some terminate (end), like 1/4 = 0.25. The nature of the decimal representation depends on the prime factorization of the denominator of the fraction. Fractions with denominators that only have 2 and/or 5 as prime factors will result in terminating decimals. Fractions with denominators containing other prime factors will result in repeating decimals.
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in many real-world applications:
- Financial calculations: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Measurements: Converting units of measurement often requires decimal conversions. For example, converting inches to centimeters.
- Scientific calculations: Many scientific formulas and equations require decimal representation of numbers.
- Data analysis: Representing data in decimal form is essential for data analysis and interpretation.
- Computer programming: Many programming languages require decimal input for various calculations.
Rounding Decimals
Since the decimal representation of 7/15 is a repeating decimal, it's often necessary to round the decimal to a certain number of decimal places. The level of precision required depends on the context. For example:
- Rounded to two decimal places: 0.47
- Rounded to three decimal places: 0.467
- Rounded to four decimal places: 0.4667
The process of rounding involves looking at the digit immediately following the desired number of decimal places. If this digit is 5 or greater, you round up; otherwise, you round down.
Advanced Concepts: Continued Fractions
For those interested in exploring more advanced mathematical concepts, the fraction 7/15 can be represented as a continued fraction. Continued fractions provide an alternative way to express rational numbers (fractions) and offer insights into their properties. While this is beyond the scope of a basic conversion tutorial, it’s a fascinating area for further exploration.
Conclusion
Converting the fraction 7/15 to its decimal equivalent (0.466̅) involves various methods, each with its own advantages and disadvantages. Long division provides a fundamental understanding of the conversion process, while calculators offer a quick and convenient solution. Understanding repeating decimals and the principles of rounding are crucial for working with these types of conversions accurately and effectively. The application of these concepts extends to various fields, highlighting the importance of mastering fraction-to-decimal conversion. Remember to choose the method most appropriate for your needs and context, and always strive for accuracy and clarity in your calculations. Further exploration into topics like continued fractions can enrich your mathematical understanding and offer alternative perspectives on number representation.
Latest Posts
Latest Posts
-
How Many Cents A Dollar
Sep 20, 2025
-
Is 12 59am A Real Time
Sep 20, 2025
-
35 110 Divided By 5x2
Sep 20, 2025
-
Convert 67 Inches To Centimeters
Sep 20, 2025
-
How Many Tablespoons Equal 30ml
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 7 15 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.