7/8x 8 - 1/2x 2
gasmanvison
Sep 24, 2025 · 5 min read
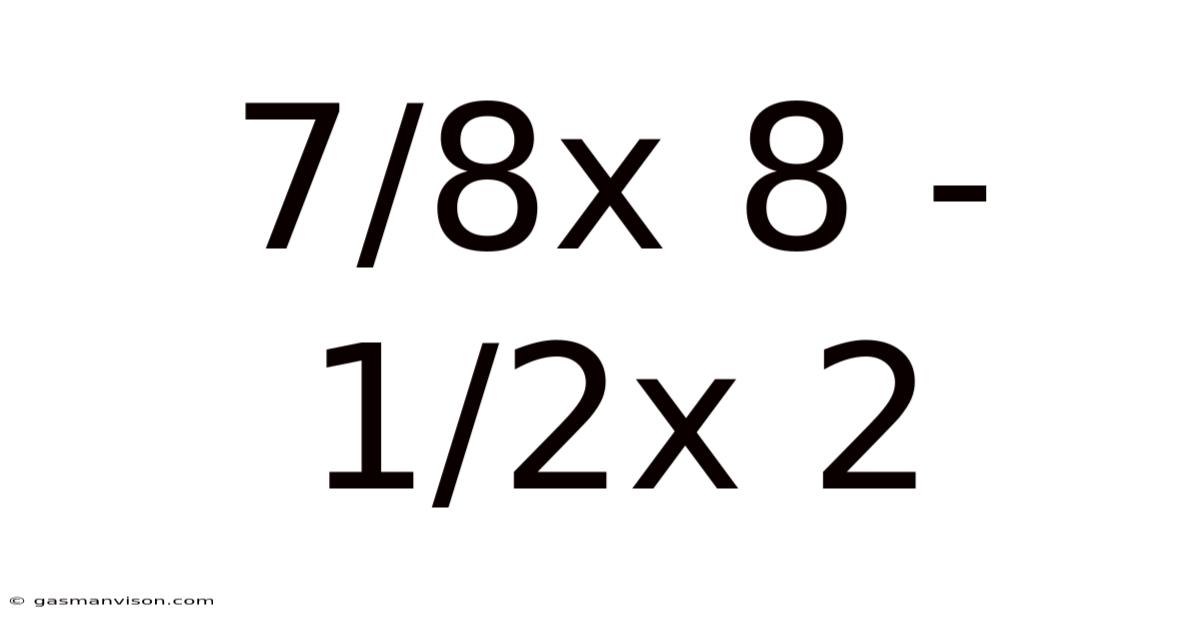
Table of Contents
Decoding 7/8x 8 - 1/2x 2: A Deep Dive into Mathematical Operations and Their Applications
This seemingly simple mathematical expression, 7/8 x 8 - 1/2 x 2, offers a fantastic opportunity to explore fundamental mathematical operations, their order of precedence (commonly known as BODMAS/PEMDAS), and their practical applications in various fields. While the solution itself is straightforward, understanding the underlying principles and expanding upon them reveals a wealth of knowledge crucial for problem-solving and analytical thinking. This article will meticulously break down the calculation, exploring the concepts involved, and providing real-world examples to illustrate their relevance.
Meta Description: Unravel the mystery behind the mathematical expression 7/8 x 8 - 1/2 x 2. This comprehensive guide explores order of operations, fraction multiplication, and real-world applications of these fundamental mathematical concepts. Learn how to solve the equation and grasp its significance beyond simple arithmetic.
Understanding the Order of Operations (BODMAS/PEMDAS)
Before diving into the solution, let's solidify our understanding of the order of operations. This fundamental principle dictates the sequence in which mathematical operations should be performed to ensure a consistent and accurate result. The acronyms BODMAS and PEMDAS are commonly used to remember the order:
- BODMAS: Brackets, Orders (powers and roots), Division and Multiplication (from left to right), Addition and Subtraction (from left to right).
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
Both acronyms represent the same order of operations; the difference lies in the terminology used. This article will use BODMAS for consistency.
In our expression, 7/8 x 8 - 1/2 x 2, we have multiplication and subtraction. According to BODMAS, multiplication takes precedence over subtraction. Therefore, we must perform the multiplications before the subtraction.
Solving the Equation: A Step-by-Step Approach
Now, let's break down the solution step-by-step:
-
Multiplication 1: 7/8 x 8
This involves multiplying a fraction (7/8) by a whole number (8). We can simplify this by canceling out the common factor of 8:
(7/8) x 8 = 7
-
Multiplication 2: 1/2 x 2
Similarly, we multiply the fraction (1/2) by the whole number (2). Again, we can simplify:
(1/2) x 2 = 1
-
Subtraction: 7 - 1
Finally, we perform the subtraction:
7 - 1 = 6
Therefore, the solution to the equation 7/8 x 8 - 1/2 x 2 is 6.
Beyond the Basics: Exploring Fractions and Multiplication
Our equation highlights the importance of understanding fractions and their multiplication. Let's delve deeper into these concepts:
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered.
-
Multiplying Fractions: To multiply fractions, we multiply the numerators together and the denominators together. For example: (a/b) x (c/d) = (a x c) / (b x d). Simplification, by canceling out common factors, is often possible before or after the multiplication, making calculations easier.
-
Multiplying Fractions by Whole Numbers: When multiplying a fraction by a whole number, we can express the whole number as a fraction with a denominator of 1. For example, multiplying 7/8 by 8 is equivalent to (7/8) x (8/1).
Real-World Applications: Where These Concepts Matter
The seemingly simple operations demonstrated in our equation are fundamental to numerous real-world applications across various disciplines:
-
Engineering and Physics: Calculations involving fractions and decimals are essential in engineering design, physics equations (like calculating forces, velocities, or accelerations), and other technical fields. Understanding the order of operations is crucial for accurate results in complex engineering computations.
-
Finance and Accounting: Fractions and percentages are ubiquitous in financial calculations. Calculating interest rates, determining profit margins, or analyzing investment returns all involve manipulating fractions and decimals, often requiring a precise understanding of the order of operations. For instance, calculating compound interest involves repeated multiplication and addition.
-
Cooking and Baking: Recipes often require precise measurements, often expressed as fractions. Accurately calculating ingredient quantities relies on a solid understanding of fractions and their manipulations.
-
Construction and Carpentry: Measuring and cutting materials accurately in construction and carpentry involves fractions and decimals extensively. Understanding fractions is crucial for ensuring precise measurements and avoiding errors.
-
Data Analysis and Statistics: Data analysis often involves manipulating numerical data, which frequently requires using fractions and decimals. Calculating averages, percentages, and other statistical measures necessitates a strong grasp of these fundamental mathematical concepts.
-
Computer Programming: Computer programming heavily relies on mathematical operations. Programmers frequently use fractions and decimals in algorithms and calculations, and a clear understanding of the order of operations is critical for writing error-free code.
Expanding the Scope: More Complex Calculations
While our example was relatively simple, the principles we've discussed can be applied to far more complex equations. Consider an equation involving multiple operations, brackets, and exponents. By systematically applying BODMAS, even the most complex calculations can be broken down into manageable steps, leading to a correct and accurate solution.
Conclusion: The Power of Fundamentals
The seemingly simple mathematical expression, 7/8 x 8 - 1/2 x 2, provides a powerful illustration of the importance of understanding fundamental mathematical concepts. Mastering fractions, multiplication, subtraction, and the order of operations (BODMAS/PEMDAS) is crucial not just for solving mathematical problems, but also for tackling numerous real-world challenges across various fields. This understanding forms the bedrock of advanced mathematical concepts and analytical thinking, empowering individuals to approach complex problems with confidence and precision. The ability to break down complex problems into smaller, manageable steps, as demonstrated with this equation, is a valuable skill applicable far beyond the realm of mathematics. Therefore, a solid grasp of these fundamentals is an invaluable asset in both academic and professional pursuits.
Latest Posts
Latest Posts
-
Biotic Factors In A Ocean
Sep 24, 2025
-
18 Out Of 22 Percentage
Sep 24, 2025
-
Alka Seltzer Water Chemical Equation
Sep 24, 2025
-
What Is 15 Of 24
Sep 24, 2025
-
Dark Wood That Neutralizes Poison
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7/8x 8 - 1/2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.