75 Of What Is 36
gasmanvison
Sep 16, 2025 · 4 min read
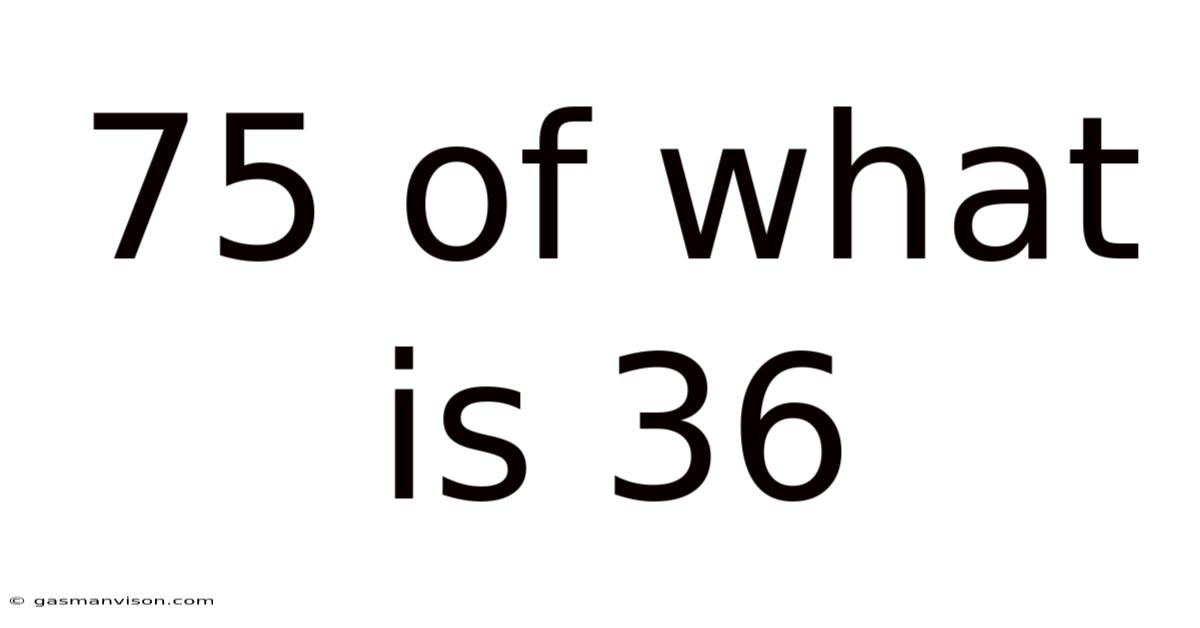
Table of Contents
Decoding the Fraction: 75 of 36 – A Deep Dive into Percentage Calculations
What is 75% of 36? This seemingly simple question opens a door to a world of percentage calculations, a crucial skill in numerous aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only answer the question but will also explore the underlying concepts, provide multiple methods for solving similar problems, and delve into the practical applications of percentage calculations. This in-depth guide aims to equip you with the tools to confidently tackle any percentage problem you encounter.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Understanding this basic definition is key to solving percentage problems. When we say "75% of 36," we're essentially asking for 75 parts out of 100 of the number 36.
Method 1: The Fraction Method – A Classic Approach
This method utilizes the fundamental definition of a percentage. We can represent 75% as the fraction 75/100. To find 75% of 36, we multiply 36 by this fraction:
(75/100) * 36 = 27
Therefore, 75% of 36 is 27.
This method is straightforward and easily understood, making it a great starting point for learning percentage calculations. It relies on the basic principles of fractions and multiplication, making it accessible even to those with limited mathematical backgrounds. The ability to convert percentages to fractions and vice versa is a foundational skill in mathematics and has numerous real-world applications.
Method 2: The Decimal Method – Efficiency and Precision
This method leverages the decimal equivalent of a percentage. To convert a percentage to a decimal, we divide the percentage by 100. 75% becomes 0.75 (75 divided by 100). We then multiply this decimal by the number we're interested in:
0.75 * 36 = 27
Again, the answer is 27. This method is often preferred for its efficiency, particularly when dealing with larger numbers or more complex calculations. The use of decimals streamlines the process and reduces the risk of errors associated with working with fractions.
Method 3: Using Proportions – A Versatile Approach
Proportions offer a more versatile approach to solving percentage problems, particularly helpful when dealing with unknown variables. We can set up a proportion as follows:
75/100 = x/36
where 'x' represents the unknown value (75% of 36). To solve for 'x', we cross-multiply:
75 * 36 = 100 * x
2700 = 100x
x = 2700 / 100
x = 27
This method highlights the relationship between the percentage, the whole number, and the part we're trying to find. It's a particularly useful technique for solving problems where the percentage or the whole number is unknown. Understanding proportions is crucial for various mathematical and scientific applications.
Method 4: The Percentage Change Calculation – Extending the Concept
While the initial question focused on finding a percentage of a number, let's expand our understanding to percentage change. Imagine a scenario where a product initially costs 36 and its price increases by 75%. To calculate the new price, we first find the amount of increase:
0.75 * 36 = 27 (increase in price)
Then, we add this increase to the original price:
36 + 27 = 63
The new price would be 63. Conversely, if the price decreased by 75%, we would subtract the calculated increase from the original price. Understanding percentage change is critical for analyzing trends, evaluating investments, and understanding economic data.
Real-World Applications: Putting Percentage Calculations to Work
The ability to calculate percentages is indispensable in numerous real-world situations. Consider these examples:
- Sales and Discounts: Calculating discounts on sale items, determining the final price after a discount is applied.
- Taxes and Tips: Calculating sales tax on purchases, figuring out the appropriate tip amount in a restaurant.
- Financial Planning: Determining interest earned on savings accounts, calculating loan payments, understanding investment returns.
- Data Analysis: Interpreting statistical data, analyzing market trends, understanding survey results.
- Scientific Research: Analyzing experimental data, expressing results as percentages, calculating error margins.
Beyond the Basics: Handling More Complex Percentage Problems
While the examples above focused on relatively straightforward calculations, percentage problems can become significantly more complex. These complexities might involve:
- Multiple Percentage Changes: Calculating the cumulative effect of multiple percentage increases or decreases.
- Compounding Interest: Understanding the growth of an investment over time due to compounded interest.
- Percentage Points vs. Percentages: Differentiating between a percentage change and a change in percentage points (a common source of confusion).
Mastering Percentage Calculations: A Continuous Journey
This comprehensive exploration of percentage calculations highlights the importance of understanding the underlying concepts and mastering multiple solution methods. From the fundamental fraction method to the more advanced approaches involving proportions and percentage change, the ability to work with percentages is a valuable skill applicable across diverse fields. Continuous practice and application are key to mastering this crucial mathematical concept. By understanding the diverse approaches and their applications, you'll not only be able to solve percentage problems effectively but also appreciate their significance in everyday life and various professional contexts. Remember that the core principle remains consistent – understanding the relationship between the percentage, the whole, and the part you're seeking to determine. With practice and a solid understanding of the underlying principles, you'll confidently navigate the world of percentages.
Latest Posts
Latest Posts
-
Inches Of Water To Psig
Sep 16, 2025
-
Convert 200 Lbs To Kilos
Sep 16, 2025
-
Science Words Beginning With I
Sep 16, 2025
-
1 4 As A Whole Number
Sep 16, 2025
-
Lewis Dot Structure For Nco
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 75 Of What Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.