7x18 45 Divided By 3x2
gasmanvison
Sep 06, 2025 · 5 min read
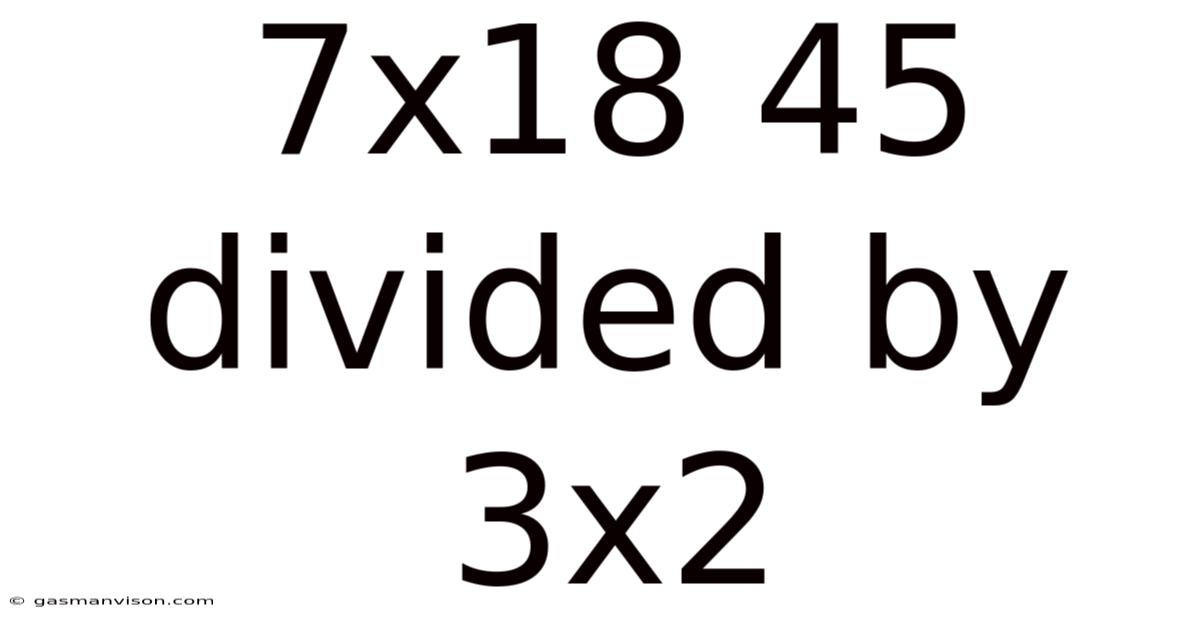
Table of Contents
Deconstructing the Mathematical Expression: 7x18 + 45 ÷ 3x2
This article delves into the seemingly simple, yet surprisingly complex, mathematical expression: 7 x 18 + 45 ÷ 3 x 2. We'll not only solve the equation but also explore the underlying principles of order of operations (often remembered by the acronym PEMDAS/BODMAS), the importance of precision in mathematical notation, and how seemingly minor variations in the expression can drastically alter the outcome. This exploration will be beneficial for anyone looking to improve their mathematical understanding, particularly students grappling with algebraic concepts and anyone interested in the nuances of mathematical interpretation.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before tackling the expression, let's establish the fundamental rules that govern mathematical operations. PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) are mnemonics used to remember the correct sequence. Both acronyms represent the same order of operations. The key takeaway is that multiplication and division have equal precedence, as do addition and subtraction. When operations of equal precedence appear, they are performed from left to right.
This seemingly simple rule is crucial for arriving at the correct answer. Ignoring it leads to erroneous results. Let's break down the provided expression step by step, adhering strictly to the order of operations:
1. Multiplication and Division (from left to right):
- 7 x 18 = 126: We begin with the first multiplication operation.
- 45 ÷ 3 = 15: Next, we perform the division.
- 15 x 2 = 30: Finally, we complete the remaining multiplication.
Our simplified expression now looks like this: 126 + 30
2. Addition:
- 126 + 30 = 156: This final addition yields the solution.
Therefore, the solution to 7 x 18 + 45 ÷ 3 x 2 is 156.
The Importance of Notation and Parentheses
The seemingly simple structure of the original expression highlights the crucial role of notation in mathematics. The absence of parentheses significantly influences the order of operations. Let's consider what would happen if we were to introduce parentheses, altering the intended sequence of calculations.
Scenario 1: (7 x 18) + (45 ÷ 3) x 2
This expression, with the use of parentheses to group operations, doesn't change the final answer. The parentheses simply reinforce the existing order implied by PEMDAS/BODMAS. We’d still arrive at 156.
Scenario 2: 7 x (18 + 45 ÷ 3) x 2
Here, the parentheses dramatically change the outcome. Following the order of operations within the parentheses first:
- 45 ÷ 3 = 15
- 18 + 15 = 33
The expression simplifies to: 7 x 33 x 2
- 7 x 33 = 231
- 231 x 2 = 462
The solution in this scenario becomes 462. This drastically different result underscores the critical role of parentheses in specifying the intended order of operations, illustrating that even slight changes in notation can significantly impact the final outcome.
Scenario 3: 7 x 18 + (45 ÷ (3 x 2))
Here, nested parentheses further demonstrate the nuances of altering the expression:
- 3 x 2 = 6
- 45 ÷ 6 = 7.5
- 7 x 18 = 126
- 126 + 7.5 = 133.5
This demonstrates that nested parentheses can create complex orders of operations that deviate even further from the original expression's result.
Practical Applications and Real-World Examples
Understanding the order of operations is not merely an academic exercise; it has significant practical applications in various fields:
-
Programming: Programming languages strictly adhere to the order of operations to execute mathematical computations within code. Incorrect order can lead to program errors and unexpected results.
-
Engineering and Physics: Engineering and physics calculations rely heavily on accurate mathematical computations, where following the order of operations is critical for obtaining correct results in structural design, circuit analysis, and other applications.
-
Finance and Accounting: Financial calculations, including compound interest, loan amortization, and investment returns, all depend on precise application of the order of operations.
-
Data Science and Machine Learning: In data analysis and machine learning algorithms, correct mathematical operations are crucial for accurate data processing, model building, and decision-making.
Common Mistakes and How to Avoid Them
Common mistakes related to order of operations often stem from:
-
Ignoring PEMDAS/BODMAS: Failing to follow the established order leads to inaccurate results. Always remember the sequence: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (left to right), Addition and Subtraction (left to right).
-
Misinterpreting Notation: Ambiguous notation can lead to misinterpretations. Always use parentheses to clarify the intended order of operations, especially when dealing with complex expressions.
-
Overlooking Left-to-Right Rule: When dealing with operations of equal precedence, remember the left-to-right rule. This ensures consistent interpretation and eliminates potential errors.
Advanced Concepts and Further Exploration
This seemingly simple arithmetic problem opens doors to more advanced concepts in mathematics:
-
Algebraic Expressions: The expression can be generalized using algebraic variables, allowing for a deeper understanding of symbolic manipulation and equation solving.
-
Functional Notation: The expression can be represented as a function, where the input is the expression and the output is the calculated value.
-
Computational Complexity: Exploring different algorithms and methods for solving similar expressions could lead to discussions on computational complexity and efficiency.
Conclusion
The mathematical expression 7 x 18 + 45 ÷ 3 x 2, despite its apparent simplicity, provides a valuable lesson in the importance of order of operations and precise notation. By systematically applying the PEMDAS/BODMAS rules and understanding the impact of parentheses, we arrive at the correct solution of 156. Furthermore, the exploration highlights the practical relevance of these seemingly basic mathematical principles in various fields, underlining their significance beyond the classroom. Remember, a thorough grasp of order of operations is essential for accurate calculations and successful problem-solving in numerous contexts. By understanding these fundamental rules and paying close attention to notation, we can approach more complex mathematical challenges with confidence and accuracy.
Latest Posts
Latest Posts
-
5 Dozen Is How Many
Sep 07, 2025
-
If Records Are Inadvertently Destroyed
Sep 07, 2025
-
5 Ft 10 To Inches
Sep 07, 2025
-
68 Kg How Many Pounds
Sep 07, 2025
-
Which Construction Is Illustrated Above
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 7x18 45 Divided By 3x2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.